6.Проекция

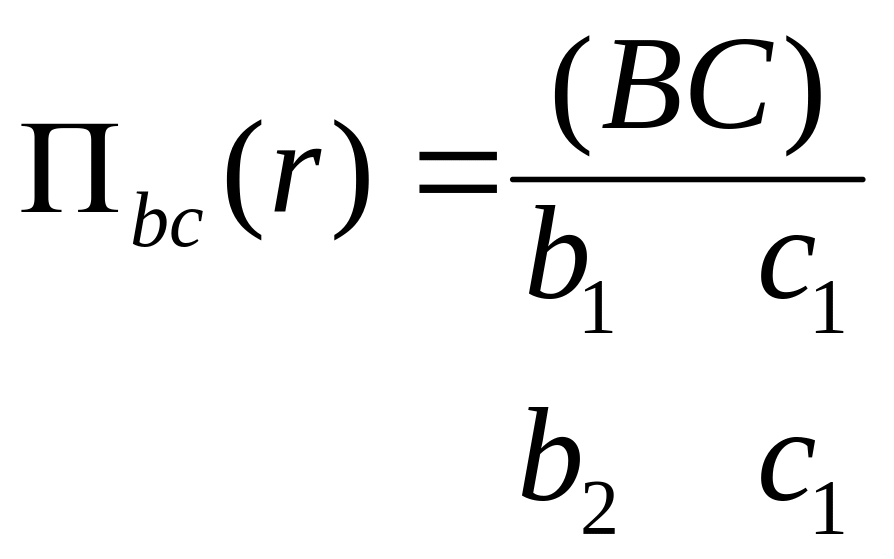
получено вычёркиванием столбцов соответствующих атрибутам в R –x и исключением из оставшихся столбцов повторяющихся строк.

7.Тетта – соединение (Θ – соединение).

8.Естественное соединение – комбинируется 2 отношения по всем их общим атрибутам.

Отношения – r(R),s(S)

Пример: ,

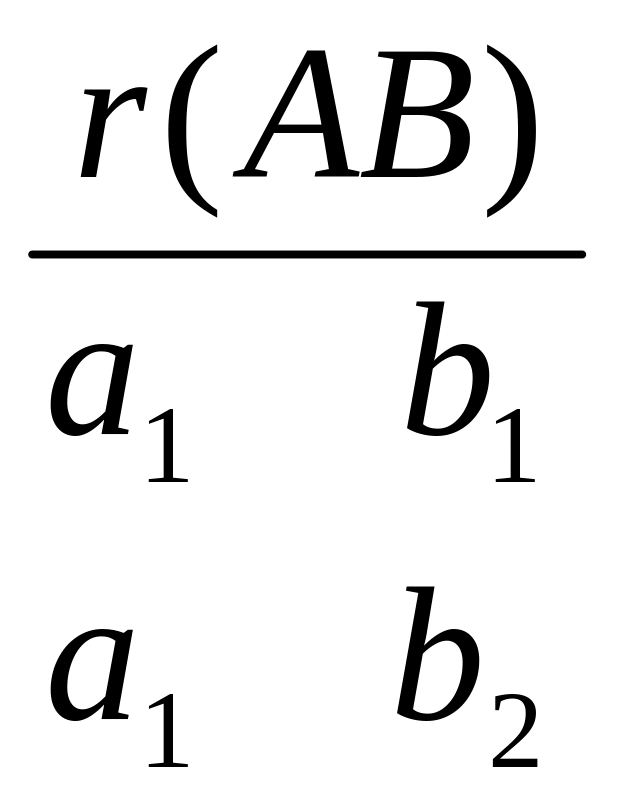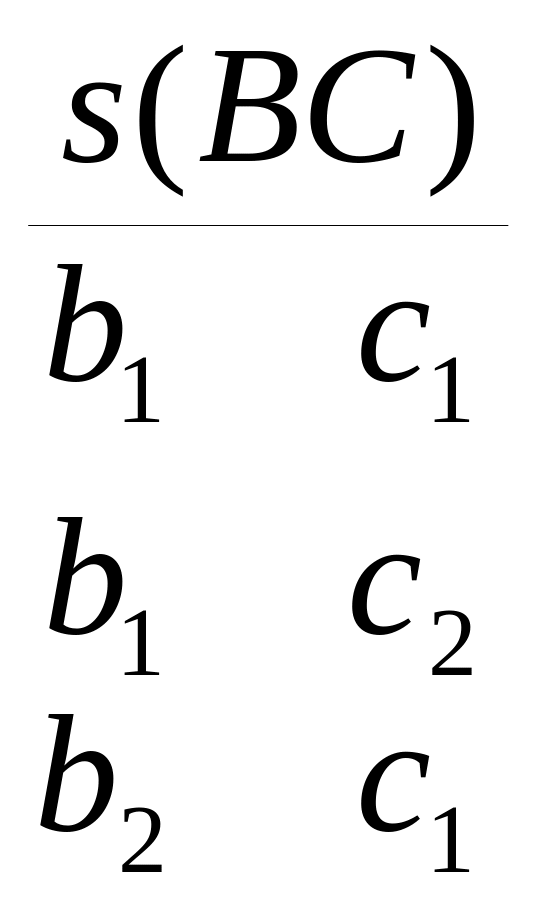
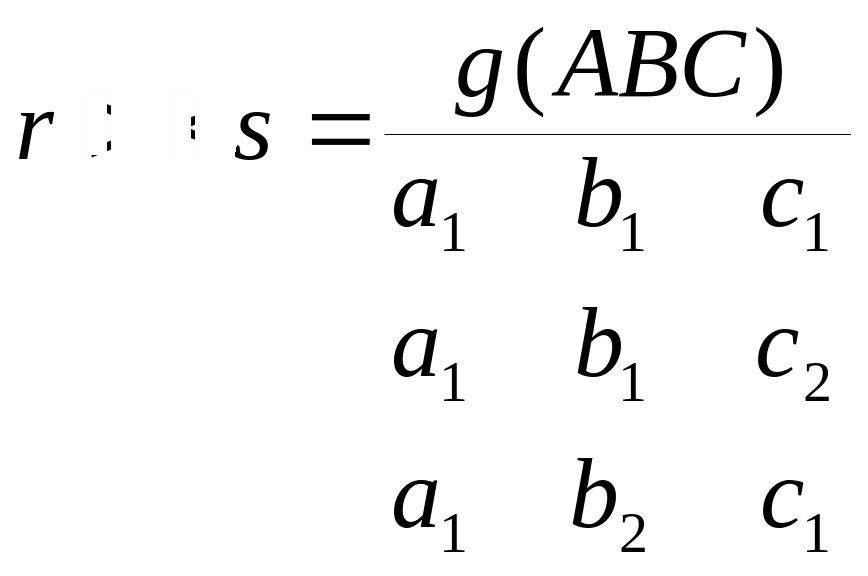
48 Оператор деления. Постоянные отношения. Переименование атрибутов, эквисоединение.

Деление

Пусть r(R) и s(S) – отношения, SR. Положим R = R - S. Тогда r, разделенное на s – это отношение r(R)={t | t_ss t_rr: t_r(R)=t & t_r(S)=t_s}.

Отношение r– частное от деления r на s, что обозначается r= rs. Иначе rs – это максимальное подмножество r множества _R (r), такое, что r  s  r. Соединение здесь – декартово произведение.

Пример

Дано отношение, отражающее право пилотирования определенных типов

Пусть заданы два множества типов самолетов, представленных в виде отношений с одним атрибутом.Для получения информации о пилотах, имеющих право пилотирования самолетов из множества q или множества s может быть использована операция деления.

Деление. r’ = r ÷ s. ,

r ÷ s =

Пилот s	Тип самолёта q
Е Е Е О О	707 727 747 707 727

, право ÷

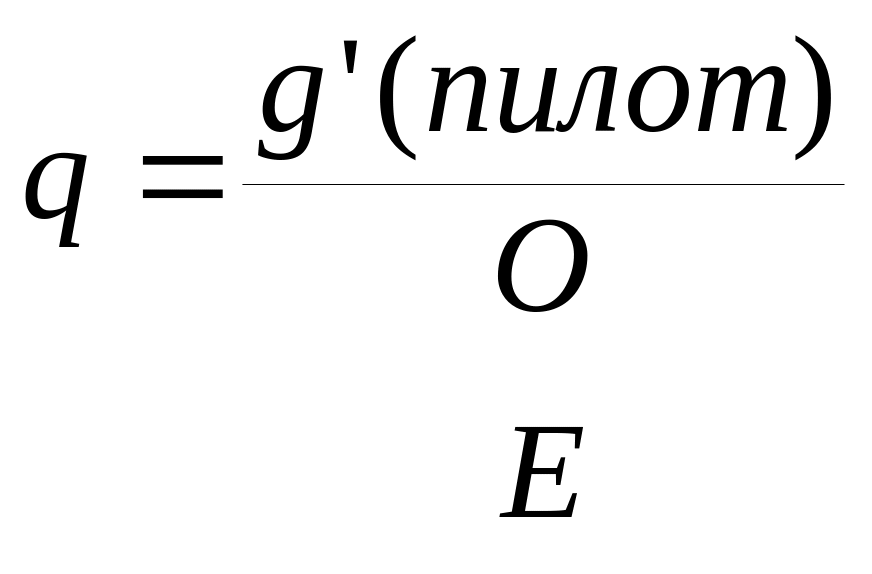
, право ÷

Постоянные отношения. Переименование атрибутов

(const в программах). Кортежи, которые не меняются – постоянные кортежи. <C₁:A₁,C₂:A₂,…>

(<E:Пилот> <707:номер самолёта>)

Постоянные отношения – множество постоянных кортежей.

Пример

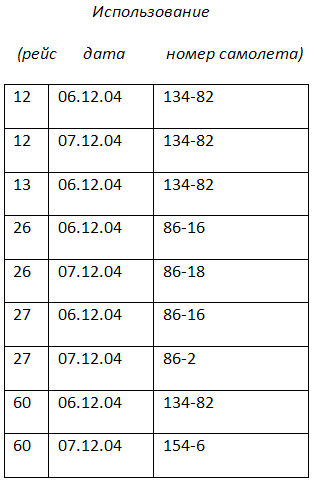
Отношение использование определяет назначение конкретного самолета с заданным бортовым номером на рейс в определенную дату.

Требуется узнать все пары рейсов, которые используют один и тот же самолет в один и тот же день. Для этого хорошо было бы соединить отношение использование с его копией, игнорируя связи по столбцу рейс. Но для этого нужно, чтобы атрибут рейс в копии назывался по-другому, например, рейс2. Переименование атрибутов производится соответствующим оператором.

Переименование атрибутов. δ_A=B(r). Имя атрибута A будет заменено на B.

Отношение с искомыми парами рейсов: --

П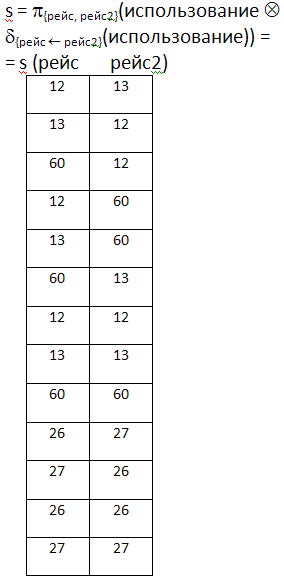 усть r – отношение со схемой R,

A₁,…, A_k  R;

B₁,…, B_k  R – (A₁…A_k); (1)

i: dom(B_i) = dom(A_i).

Обозначим одновременное переименование атрибутов A₁,…, A_k в B₁,…, B_k как _{A1,…, Ak  B1,…, Bk}(r). оно всегда может быть записано в виде последовательности переименований. Если это условие не выполняется, без введения дополнительных атрибутов такую замену выполнить нельзя. Очевидный пример – обмен _{A, B  B, A} .

Эквисоединение,

-Соединение по условию: r[условие]r – условие только типа равенство.

r [A₁ = B₁, A₂ = B₂,…, A_m = B_m] s.

В эквисоединении все атрибуты различаются по именам, то есть, чтобы RS = . Это не сильное ограничение, так как путем переименования атрибутов в s и r можно добиться пустого пересечения их схем.

Если в эквисоединении нет сравнений, то оно совпадает с декартовым произведением: r [ ] s = r  s.

Соединение, определённое ранее, иногда называют естественным.

Эквисоединение может быть выражено через переименование и естественное соединение

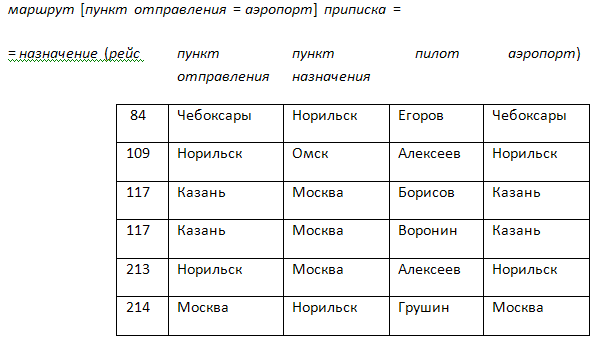
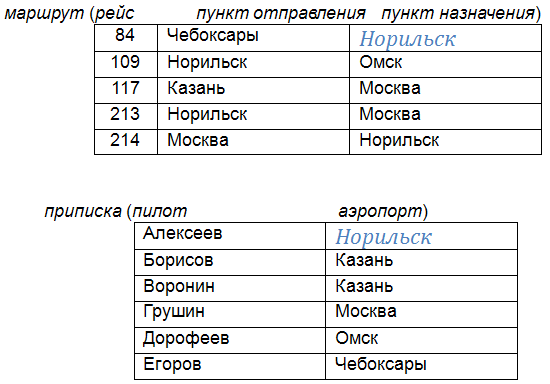
Пр:Заданы отношения маршрут, в котором указаны аэропорты отправления и назначения авиарейсов, и приписка, которое определяет аэропорт, где работает пилот. Следует назначить пилотов на рейсы из аэропорта их приписки. Задача решается эквисоединением по столбцам пункт отправления и аэропорт.