1.2. Математическое описание электропривода с асинхронным двигателем и разомкнутой системой регулирования в среде matlab- Simulink

В учебнике [Л1] приведена исходная система уравнений для проекций пространственных векторов, в которой действуют векторы, записанные в неподвижной системе координат x-y, и которые вращаются с угловой скоростью _0эл относительно неподвижной системы координат, и векторы в системе координат d-q , которые вращаются с угловой скоростью _р, равной частоте роторной ЭДС, относительно системы координат, вращающейся вместе с ротором:

Для дальнейшего использования их надо привести все переменные к одной системе координат.

1. Описание в неподвижной системе координат х-у.

Для получения этого описания надо в исходном уравнении перейти от переменных, записанных в системе d-q, связанной с ротором, к переменным в системе, связанной со статором.. На примере потокосцепления ротора этот переход имеет вид

В результате уравнения в системе координат х-у получаются в виде

Из двух последних уравнений можно записать

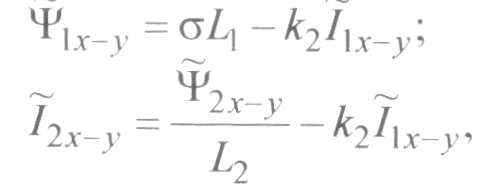
Подстановка этих выражений в два первых равенства системы позволяет после перехода к проекциям на оси координат х-у получить формулы, для построения структурной схемы в неподвижной системе координат:

Эти выражения дополняются формулами для электромагнитного момента и основного уравнения механики:

Соответствующая структурная схема приведена на рис.1. Входными воздействиями являются проекции пространственного вектора задания напряжения на статоре ; и момент нагрузки M_c. Выходными переменными служат проекции тока статора и потокосцепления ротора на оси неподвижной системы координат ,

. Их амплитудные значения могут быть вычислены по формулам и .

Расчетная схема асинхронного двигателя в неподвижной системе координат, выполненная в среде MATLAB Simulink, со значениями параметров, приведенными в [Л1] приведена на рис.2.

1.2.2. Описание электропривода с асинхронным двигателем в системе координат α-β, вращающейся с синхронной скоростью.

В тех случаях, когда по тем или иным причинам целесообразнее работать с моделью, выполненной во вращающейся системе координат, можно воспользоваться математическим описанием, приведенным в [Л1] в виде структурной схемы рис.2.2, на которой выходными переменными являются проекции потокосцеплений статора и ротора . В отличие от этого в структурной схеме рис.4 выходными переменными являются проекции токов статора и ротора. Для получения этой структурной схемы надо воспользоваться системой уравнений (1.23) в [Л1], записанной в системе координат α-β и в первые два равенства подставить выражения для потокосцеплений. После перехода к проекциям векторов на оси координат и введения обозначений и будет получена система уравнений:

. Рис.1. Структурна схема асинхронного двигателя в неподвижной системе координат

Рис.2. Расчетная схема асинхронного двигателя в неподвижной системе координат.

Файл в Simulink’е: AD_nepodw_sk

_{по которой построена структурная схема рис.4. Электромагнитный момент двигателя рассчитывается по формуле (2.10) в [Л1]:}

В структурной схеме не зафиксировано расположение вращающейся системы координат относительно вращающейся с той же скоростью системы пространственных векторов. Частным случаем является направление вектора напряжения по оси α, когда u_1α=U₁, u_1β=0.

Рис.3.Структурная схема асинхронного двигателя во вращающейся системе координат при произвольном повороте системы координат относительно системы векторов

Рис.4. Расчетная схема асинхронного двигателя во вращающейся системе координат/

Файл в Simulink’е: Model AD4