1. Basic concepts and definitions of differential equations.

Equation of the I-th order solved through derivative has the general form: y′ = f (x, y) , (1) where f (x, y) is defined and continuous in a plane domain G (G is an area which is open or a closed connected subset on the plane).

Equation (1) can be written as dy-f (x, y )dx=0, (2) i.e. in differential form. Along with (1) we consider the equation M (x, y)dx + N (x, y)dy = 0 (3) where M €C (G), N € C ( G) called the equation of the first order in differential form, or in differentials. Equation (3) can be written as permitted by the derivative: 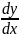= 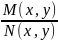at conditions that N (x, y) is not equal to zero. Equation (3) is more general than(1). It is more convenient in the sense that the variables x, y involve as equal. It's a natural fact in geometrical problems. We say that the differential equations (1) or (3) are solvable explicitly if their solutions are expressed in terms of elementary functions. Find explicit solutions of differential equations are rarely, in exceptional cases. Even a simple differential equation y’= f (x, y) leads, in general, to solutions, unexpressed in terms of elementary functions. Its solution can be written as an integral or, as it is said, "it is expressed by quadrature."

We say that the solution of the differential equation is found in quadrature, if it is expressed in terms of elementary functions and the quadrature of explicit functions. This solution is called solution in the quadratures, and the equation is soluble quadratures. Description of the equations solved in quadratures and recipes of their decisions are content of so-called elementary methods of integration.

2. Equations with separated variables.

Equations of the form y1 = f (ax + by + c)

The differential equation of the form f₁ ( y)dy = f₂ (x)dx (1) is called the equation with separated variables. We assume that the functions f₁ (y) and f₂ (x) continuous in G = {(x, y); a < x < b, c < y < d }. Expression

∫f ₁( y)dy − ∫f ₂(x)dx = C gives the general solution of (1) in the canonical form. Solution of Cauchy problem with initial data (x_0, y₀) is given by formula 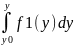– = 0 Equation of the form y`= 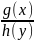(2 ) where g(x) and h( y) are continuous functions in the field G , and h( y) is non-zero at condition y € ]c,d[ called the equation with separable variables. Equation with separable variables in the differential form can be written as

ф1(x)Ψ1(y)dx= ф2(x)Ψ1(y)dy (3 ) (ф1(x) -1 это индекс)

Equation (2) is reduced to the equation of the form (1) by multiplying it by h( y)dx , and the equation (3) is reduced to equation (1) by dividing into ф1(x)Ψ1(y) division on ф1(x)Ψ1(y) can lead to the loss of some of the decisions

3. Linear equations of the first order.

Linear differential equation of the first order is an equation in which the unknown function and its first

derivative are included in the first degree: + p(x)y = q(x) (1)

We consider two solution methods of the equation: the method of Bernoulli and the method of variation of arbitrary constant.

Bernoulli’s method

Solution by using the change of variable(unknown function)of the form. y = uv, (2)

where u = u (x), v = v (x) are differentiable functions in some domain of x.

Differentiating (2) we get to the conclusion, that the general solution of the inhomogeneous linear differential equation (1) is equal to the sum of general solution of the corresponding homogeneous equation and a particular solution of the inhomogeneous equation (1) Yg.i=Yg.h+Yp.i

Darboux equation is called the equation of the form:

M(x, y)dx + N(x, y)dy + P(x, y)[xdy − ydx] = 0 (3), where M and N are homogeneous functions of degree m. P (x, y) is a homogeneous function of degree l, l ≠ m −1

Darboux equation (3) can be integrated in quadrature with the substitution y = zx, where z is a new unknown function. With this change Darboux equation is reduced to equation with separated variables, if N (x, y) = 0.

Cauchy problem and the existence and uniqueness theorem

Existence theorem. If in the equation у’=ƒ(х,у) the function ƒ is defined and continuous in abounded domain D of the plane (x, y), then for any point (х0, у0) €D exists a solution y (x) of the initial problem

dx/dy = f (x, y), у(х0)=у0, (4) defined on some interval containing х0.

Existence and uniqueness theorem. If the function ƒ is defined and continuous in a bounded domain D of the plane (x, y), and it satisfies in D to Lipschitz condition in the variable y, i.e.

| ƒ(х,у1)- ƒ(х,у2)| ≤ L|у2-у1|, (5) where, L is positive constant, then for any point

(х0,у0) €D exists a unique solution у(х) of the initial problem (4), defined on some interval containing х0.

Extension Theorem. At the conditions of the existence theorem or the theorem of the existence and uniqueness an any solution of the Cauchy problem (3.4) with initial data (х0,у0) €D can be extended to a point arbitrarily close to the boundary of D. In the first case, the continuation, in general, is not necessarily unique; in the second case it is unique.

4. Bernoulli’s method.

Linear differential equation of the first order is an equation in which the unknown function and its first

derivative are included in the first degree: + p(x)y = q(x) (1)

Bernoulli’s method

Solution by using the change of variable of the form. y = uv, (2)

where u = u (x), v = v (x) are differentiable functions in some domain of x.

Differentiating (2) we get to the conclusion, that the general solution of the inhomogeneous linear differential equation (1) is equal to the sum of general solution of the corresponding homogeneous equation and a particular solution of the inhomogeneous equation (1) Yg.i=Yg.h+Yp.i

This fact is a reflection of the general properties of solutions of linear differential equations. Note that if you can "guess" a particular solution of (1), then the search for general solutions easy.

Darboux equation is called the equation of the form:

M(x, y)dx + N(x, y)dy + P(x, y)[xdy − ydx] = 0 (3)

where M and N are homogeneous functions of degree m. P (x, y) is a homogeneous function of degree l, l ≠ m −1