6.2. Расчет приведенных моментов инерции.

Инертные свойства машин и механизмов характеризуют приведенной массой, либо приведенным моментом инерции, в зависимости от того, линейным или угловым является перемещение звена приведения.

Приведенный к звену момент инерции масс звеньев механизма вычисляют как сумму произведений масс этих звеньев и их моментов инерции на квадраты передаточных функций в движениях звеньев относительно звена приведения.

Приведенный к валу кривошипа АВ момент инерции – сумма приведенных моментов инерции следующих механизмов:

1. Зубчатой передачи

где приведенный к валу водила Н момент инерции планетарного механизма зубчатой передачи.

Величину вычисляем, пользуясь рис.6.1.

Рис.6.1. Кинематика планетарного механизма.

где

Таким образом

J_пл = 0.926 + 0.001807 ^.8,0² +3·(16.069 ^. 0.18² + 0.146 ^. 1.333²)=3,382 кгм²

2. Приведенного к валу кривошипа момента инерции кулачкового механизма . Указанный момент оказывает наибольшее влияние на движение звена приведения лишь в периоды движения толкателя кулачкового механизма – на фазах удаления и возвращения. Причем, на концах этих фаз приведенный момент толкателя т.к. передаточная функция от толкателя к кулачку. т. е. к валу кривошипа ОА, при этом равна 0.

Максимальное значение приобретает вблизи середины этих фаз, когда В этом положении величина приведенного момента инерции механизма равна

Эти положения кулачкового механизма находятся согласно циклограмме работы машины между 0 и 1, а также около 3-го положения кривошипа. Для всех положений кривошипа принимаем

3. Приведенного к валу кривошипа АВ момента инерции несущего механизма (рис. 6.2.)

Строим планы скоростей механизма по следующим уравнениям:

кривошип ОА (звено 1) совершает вращательное движение с угловой скоростью

скорость точки А: и при этом

шатун АВ (звено 2) совершает плоскопараллельное движение

скорость точки В: , где

Рис. 6.3. Рычажный механизм

ползун (звено 3) совершает поступательное движение

скорость точки В:

Точка s₂ делит отрезок аb пополам, как и точка S₂ на шатуне АВ.

Планы скоростей строим с масштабным коэффициентом .

Отрезок

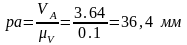
Теперь

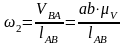
Результаты построений и расчетов сводим в таблицу:

Таблица 6.2

№ пол.	ab мм	pb мм	ps2 мм	м/с	VBA м/с	VS2 м/с	м/с
0	36,4	0	18,2	0	3,64	1,82	23,083
1	27	34	32	3,4	2,7	3,2	17,089
2	0	36,4	36,4	3,64	0	3,64	0
3	27	17	27	1,7	2,7	2,7	17,089
4	36,4	0	18,2	0	3,64	1,82	23,083
5	27	17	27	1,7	2,7	2,7	17,089
6	0	36,4	36,4	3,64	0	3,64	0
7	27	34	32	3,4	2,7	3,2	17,089
8	0	0		0

Результатами табл.6.2. пользуемся для определения моментов инерции масс подвижных звеньев механизма. В таблицу 6.3, помещаем также сведения об изменении моментов инерции масс звеньев прочих механизмов объединенных трансмиссией (кулачковый механизм, планетарный редуктор c зубчатой парой)

Таблица 6.3

№ Положения поршня	0	1	2	3		5	6	7
	0,011	0,058	0,058	0,024	0,011	0,024	0,058	0,011