4. Метрические характеристики графа

40. Пусть – связный граф, а и – две его несовпадающие вершины. Длина кратчайшей цепи называется расстоянием между вершинами и и обозн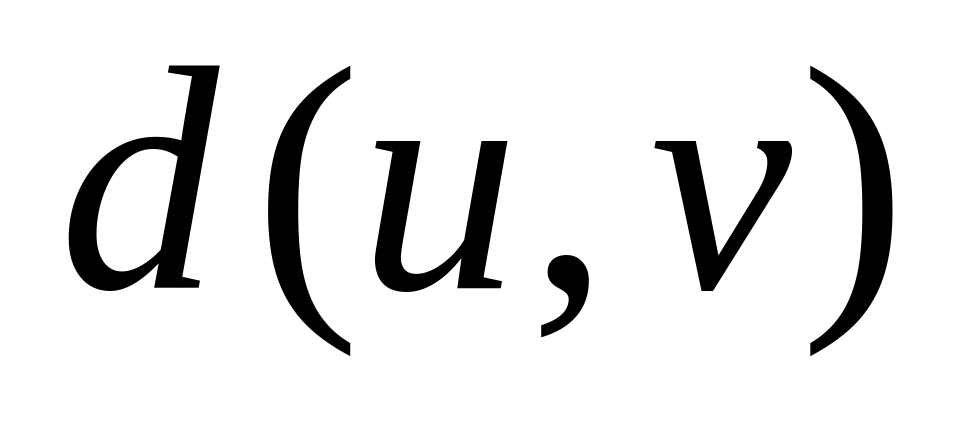ачается , а сама кратчайшая цепь обозначается и называется геодезической.

Положим, что . Если не существует цепи, то .

41. Для фиксированной вершины величина 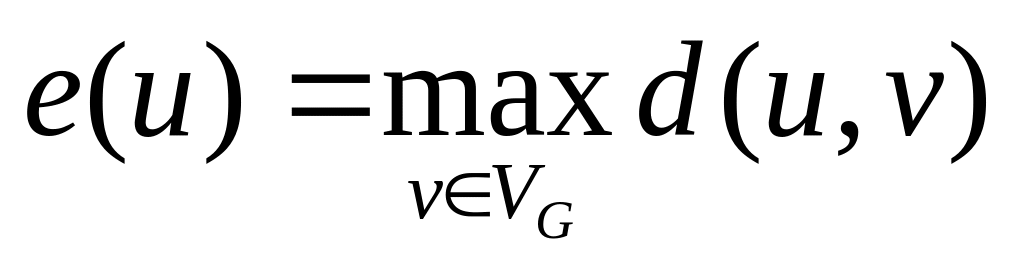называется эксцентриситетом вершины .

42. Максимальный среди всех эксцентриситетов вершин называется диаметром графа и обозначается через 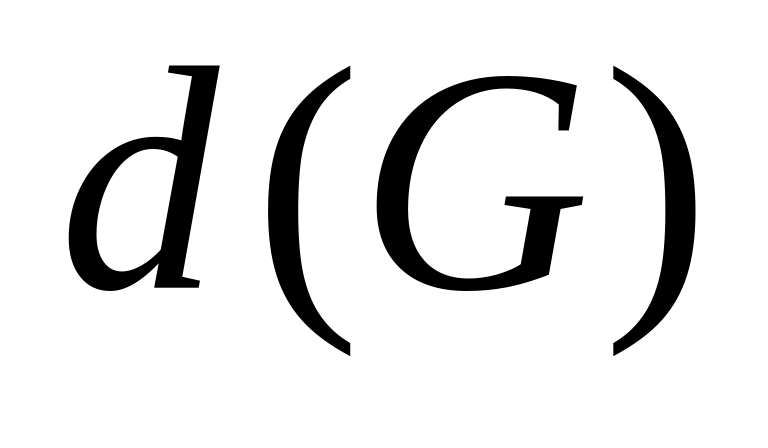. Тем самым .

43. Вершина называется периферийной, если 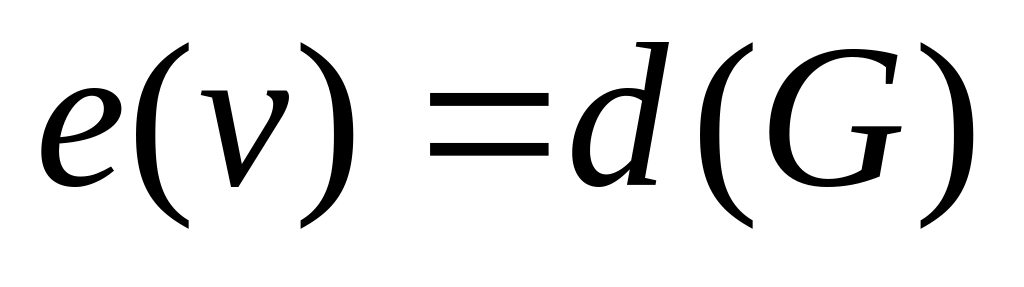. Простая цепь длины называется диаметральной цепью.

16. Рассмотрим граф:

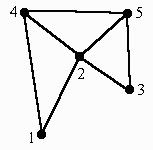
Для него , , , , . Все вершины являются периферийными, кроме второй. (1,2,3) – диаметральная цепь.

44. Минимальный из эксцентриситетов вершин связного графа называется его радиусом и обозначается через :

.

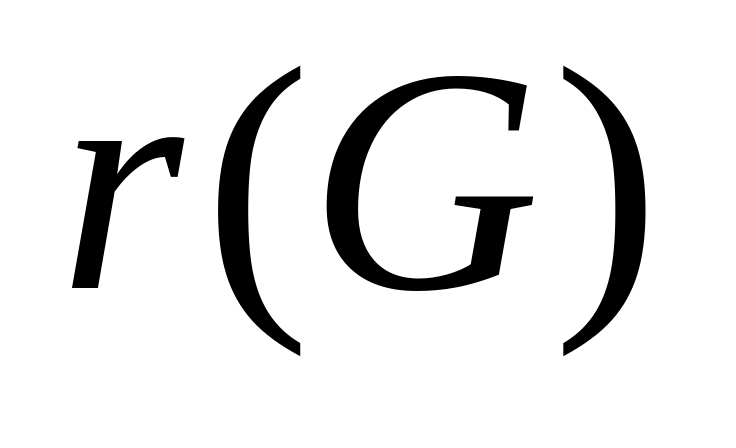45. Вершина называется центральной, если . Множество всех центральных вершин графа называется его центром.

Граф может иметь единственную центральную вершину или несколько центральных вершин. Наконец, центр графа может совпадать с множеством всех вершин. Например, центр простой цепи при четном числе вершин состоит ровно из двух вершин, а при нечетном числе вершин – из одной, для цикла все вершины являются центральными.

Метрические характеристики графа удобно определять с помощью матрицы расстояний размера :

.

Замечание. Если граф несвязный, то все метрические характеристики находятся для каждой компоненты связности отдельно.

5. Виды графов и операции над графами

   1. Виды графов

• Граф называется полным, если любые две его вершины смежны. Полный граф порядка обозначается символом 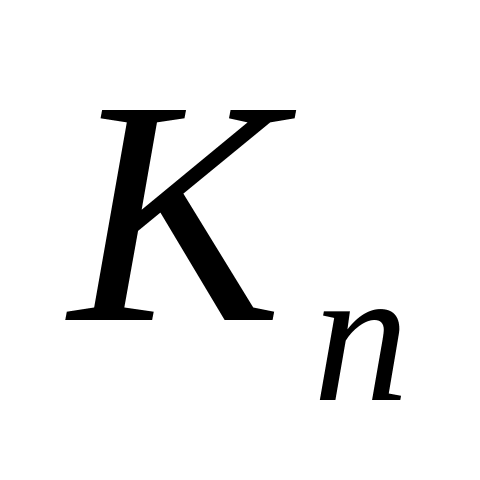. Число ребер в нем равно .

17. Полные графы – :

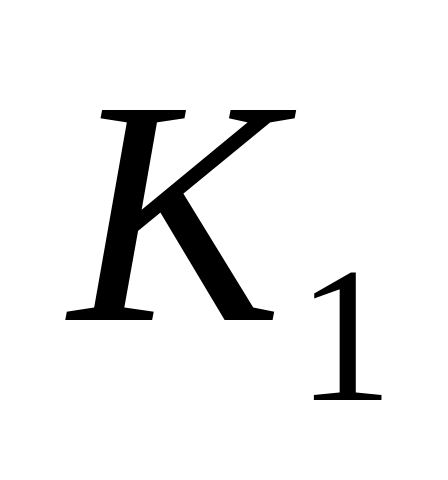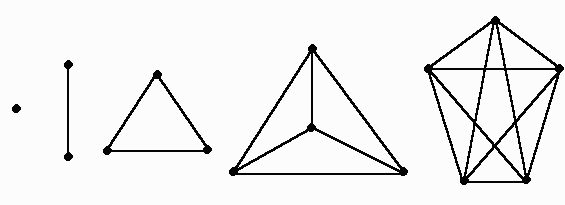
• Граф называется пустым, если в нем нет ребер. Пустой граф порядка обозначается символом .

18. Пустой граф :

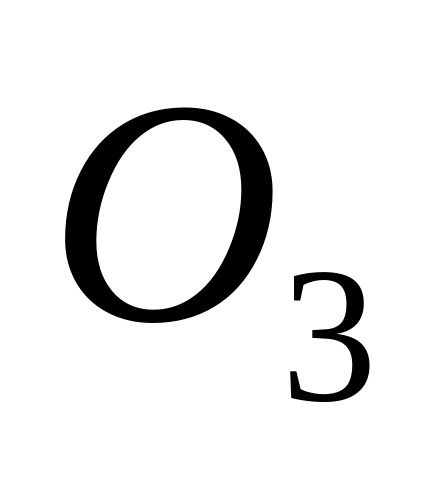• Простая цепь . , .

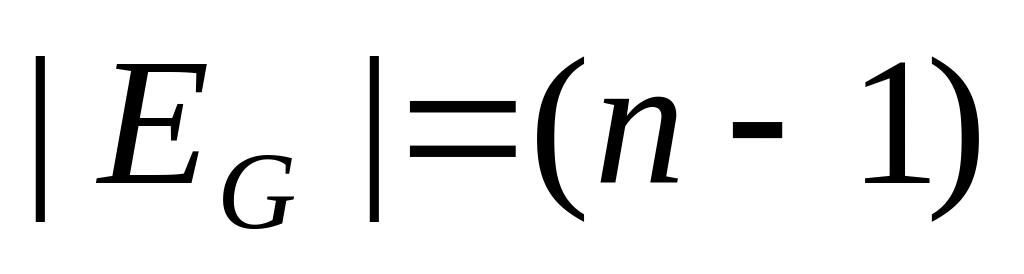19. Простые цепи – :

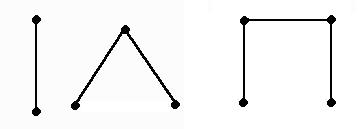
• Простой цикл . , .

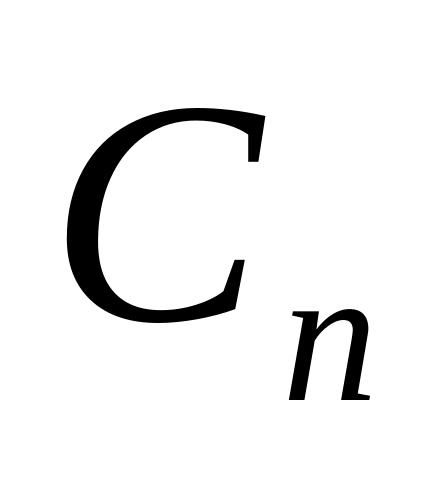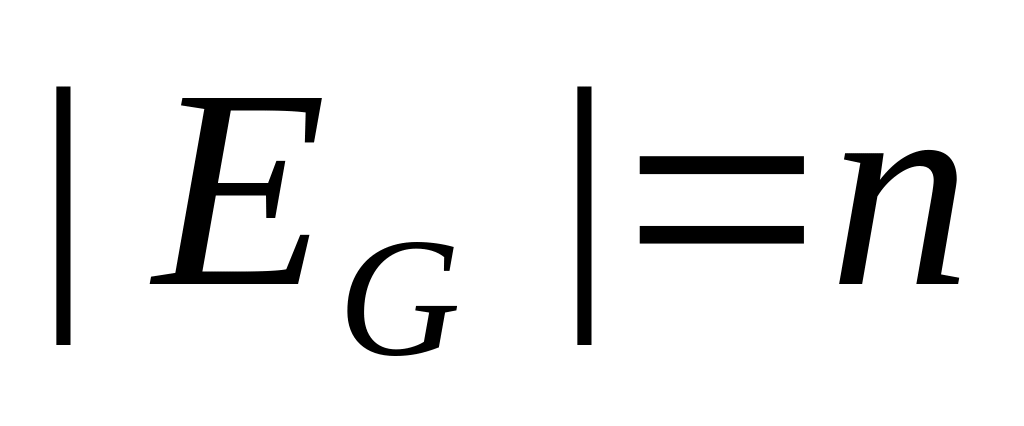20. Простые циклы – :

• Граф называется двудольным, если существует такое разбиение множества его вершин на два непересекающихся множества 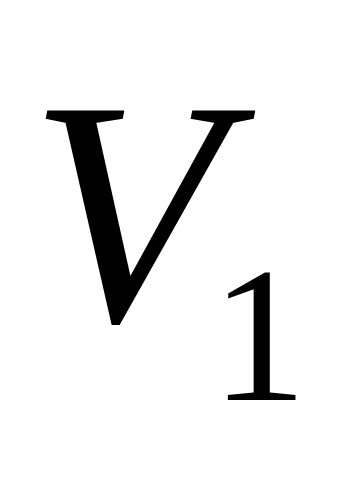и ( и 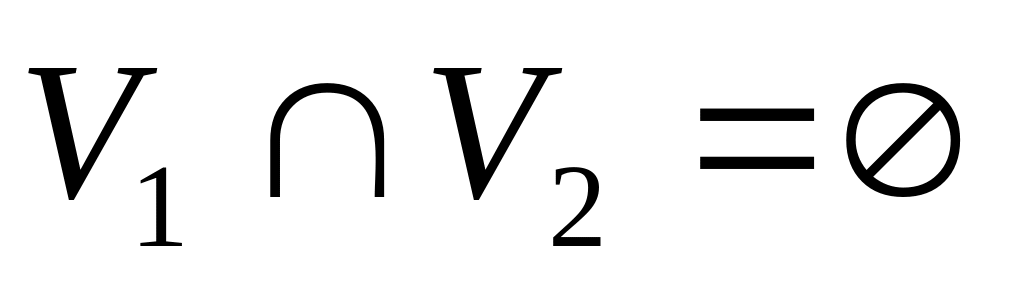), причем всякое ребро из инцидентно вершине из и вершине из (т.е. соединяет вершину из с вершиной из ).

Множества и называются долями двудольного графа. Двудольный граф, доли которого состоят из и вершин, обозначается символом .

Если при этом любые две вершины, входящие в разные доли, смежны, то граф называется полным двудольным. Полный двудольный граф, доли которого состоят из и вершин, обозначается символом .

21. Двудольный граф 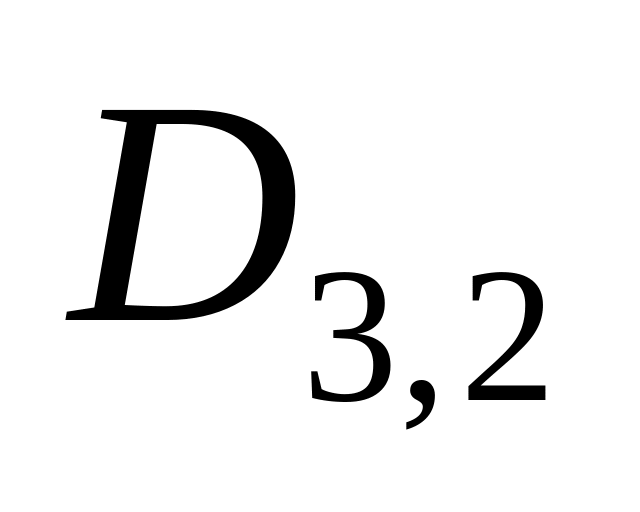и полный двудольный граф :

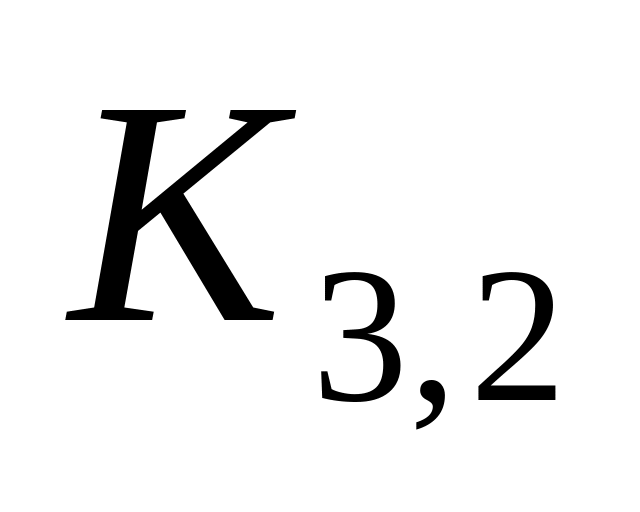4. Граф является двудольным тогда и только тогда, когда все его простые циклы имеют четную длину.

Необходимость. От противного.

Пусть - двудольный граф, и - простой цикл нечетной длины. Пусть , , …, . Тогда и эти вершины смежны, т.е. . А это противоречит двудольности.

Достаточность. Пусть в графе есть только циклы четной длины. Докажем, что он двудольный. Можно считать, что - связный граф, поскольку каждую компоненту связности можно рассматривать отдельно. Разобьем множество на и следующим образом.

Любую вершину поместим в первую долю . Вторая доля пока пустая.

Далее перебираем все остальные вершины графа . Если - четно, то , иначе .

Далее от противного. Пусть есть две вершины в одной доле, соединенные ребром. Пусть для определенности и .

Рассмотрим геодезические цепи и . Тогда длины и нечетны. Эти цепи имеют хотя бы одну общую вершину . Рассмотрим еще одну общую вершину этих цепей и обозначим ее (возможно, ). Тогда:

- четно,

и цикл - простой цикл нечетной длины , что противоречит условию.

Если же , т.е. и четны, и . Тогда также - простой цикл нечетной длины.