3. Маршруты, цепи, циклы

20. Чередующаяся последовательность:

вершин и ребер графа, такая что , , называется маршрутом, соединяющим вершины и (или -маршрутом).

Очевидно, для обычных графов маршрут можно задать последовательностью его вершин:

,

а также последовательностью ребер:

.

21. Маршрут называется цепью, если все его ребра различны. И простой цепью, если все его вершины, кроме, возможно, крайних, различны.

22. Маршрут называется циклическим, если . Циклическая цепь называется циклом, а циклическая простая цепь – простым циклом.

23. Число ребер в маршруте называется его длиной.

8. Рассмотрим граф:

В нем (1,2) и (1,2,4,7) являются простыми цепями; (1,2,4,7,8,4) – цепь, не являющаяся простой; (1,2,4,7,8,4,2) – маршрут, не являющийся цепью; (1,2,4,1) – простой цикл; (1,2,4,7,8,4,1) – цикл.

3. Связность

   1. Связные графы. Компоненты связности

24. Граф называется связным, если любые две его несовпадающие вершины соединены цепью.

9. Связный граф:

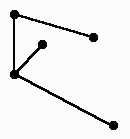
10. Несвязный граф:

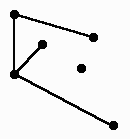
25. Всякий максимальный связный подграф графа называется компонентой связности графа . Слово «максимальный» означает, что он не содержится в связном подграфе с бо’льшим числом элементов.

11. Граф, содержащий 3 компоненты связности:

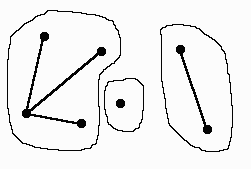
26. Множество вершин компоненты связности называется областью связности графа.

1. Для любого графа либо он сам, либо его дополнение является связным.

1. Пусть – несвязный граф, – одна из его областей связности, . Тогда для любых и в дополнительном графе есть ребро . Следовательно, произвольная вершина из соединена с маршрутом длины 1, а каждая вершина из (отличная от ) соединена с маршрутом длины не более чем 2. Из определения вытекает, что связен.

2. Пусть – связный граф, . Тогда:

• если ребро принадлежит какому-нибудь циклу графа , то граф связен;

• если ребро не входит ни в какой цикл, то граф имеет ровно две компоненты.

• Пусть ребро принадлежит циклу графа . Заменив в каждой -цепи, содержащей , подцепь -цепью , получим -маршрут, не содержащий ребра . Следовательно, в графе любые две несовпадающие вершины соединены маршрутом, не проходящим через . Но тогда и граф связен.

• Пусть ребро не входит ни в какой цикл графа . Тогда, очевидно, вершины и принадлежат разным компонентам связности графа , например, и соответственно. Для произвольной вершины в существует -маршрут. Если ребро в этот маршрут не входит, то . В противном случае .

2. (О числе ребер в графе) Если число компонент связности графа -го порядка равно , то

,

3. -число ребер.

3. Вначале рассмотрим верхнюю оценку. Пусть – граф порядка с компонентами и максимальным для таких графов числом ребер. Тогда каждая его компонента является полным графом. Пусть далее и – две компоненты, , – вершина из второй компоненты. Удалив из графа все ребра, инцидентные вершине , и сединив ребром с каждой вершиной из первой компоненты, получим новый граф порядка с тем же числом компонент и большим числом ребер. Последнее невозможно, стало быть, только одна из компонент может иметь порядок . Он равен , и поэтому:

.

Докажем нижнюю оценку : . Оно очевидно при , т.к. . Воспользуемся индукцией по . Пусть и пусть для графов с меньшим, чем , числом ребер соответствующее неравенство верно. Рассмотрим граф , где . Согласно Лемме 2, число компонент этого графа равно или . Число ребер в нем . По индуктивному предположению, в обоих случаях . Следовательно, .