
- •Правила дифференцирования. Производные степенных, тригонометрических, показательных и логарифмических, сложных и обратной функций
- •Правила дифференцирования
- •Правила дифференцирования, доказательство и примеры.
- •Элементы множества.Основные понятия. Примеры множеств
- •Пример:
- •Свойство операций над множествами
- •Определения графов
- •Основные определения
- •Другие определения графов
- •Изоморфизм графов
- •Матрицы смежности и инцидентности
- •Элементы графов
- •Подграфы
- •Степени вершин графа
- •Маршруты, цепи, циклы
- •Связность
- •Связные графы. Компоненты связности
- •Вершинная и реберная связность
- •Двусвязные графы
- •Связность в орграфах
- •Метрические характеристики графа
- •Виды графов и операции над графами
- •Виды графов
- •Реберный граф
- •Операции над графами
- •1. Основные понятия теории вероятностей. Классическое, статистическое и геометрическое определения вероятности, свойства вероятности.
- •1)Основные понятия теории вероятностей.
- •5)Геометрическое определение вероятности.
- •1.4. Введение в логику высказываний Высказывания и операции над ними
- •[Править]Методы
- •[Править]Варианты округления 0,5 к ближайшему целому
- •[Править]Применения
- •[Править]Использование округлений при работе с числами ограниченной точности
- •[Править]Эмпирические правила арифметики с округлениями
Изоморфизм графов
Говорят, что два графа
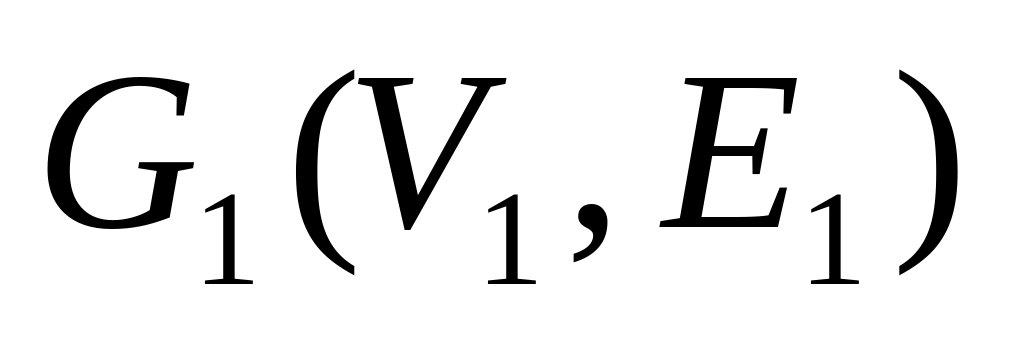 и
и
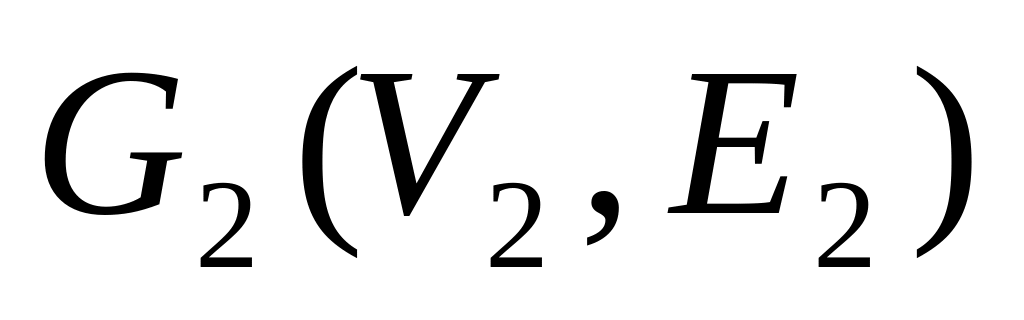 изоморфны (обозначается
изоморфны (обозначается
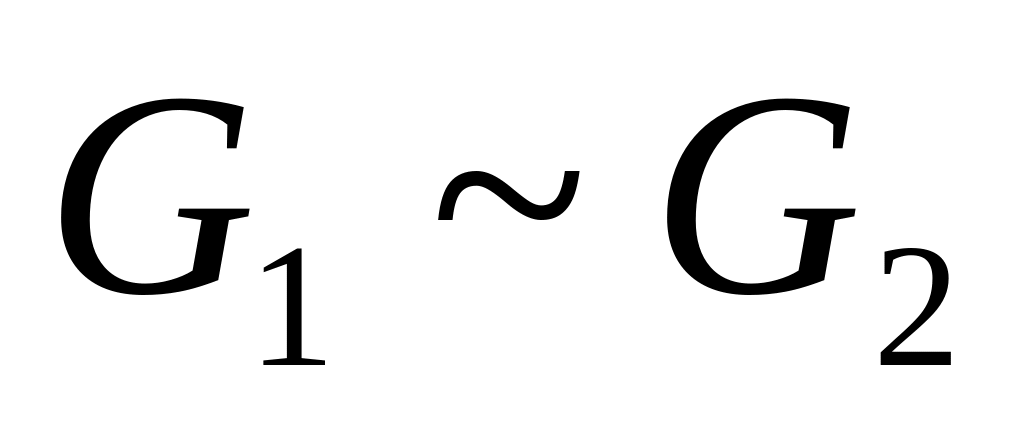 ),
если существует биекция
),
если существует биекция
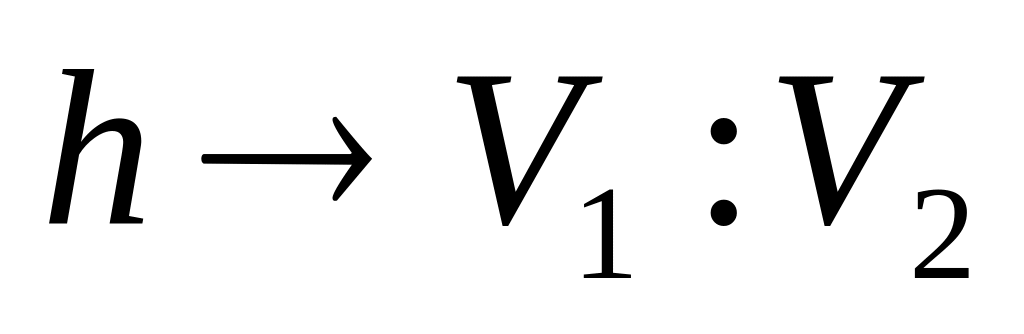 ,
сохраняющая смежность. Т.е., если есть
ребро
,
сохраняющая смежность. Т.е., если есть
ребро
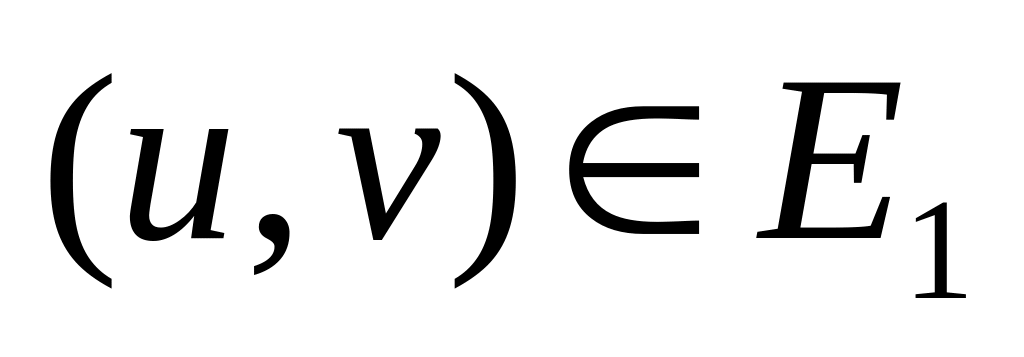 ,
то есть и ребро
,
то есть и ребро
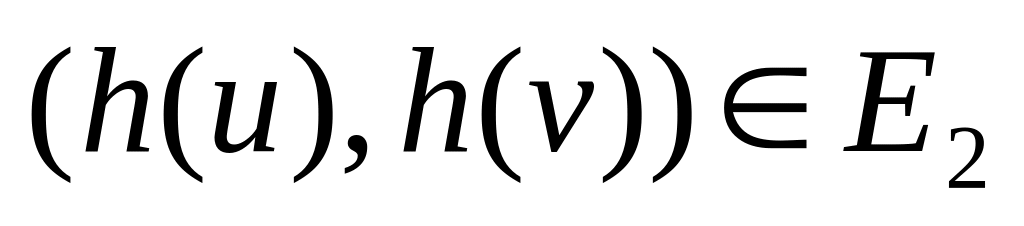 .
И наоборот, если есть ребро
.
И наоборот, если есть ребро
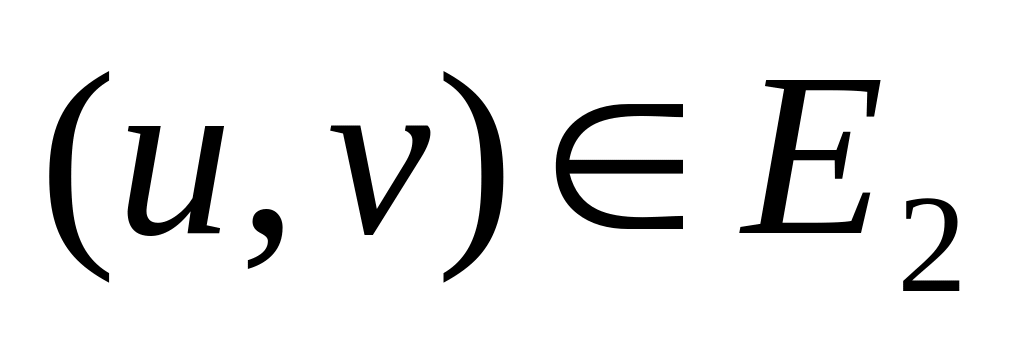 ,
то есть и ребро
,
то есть и ребро
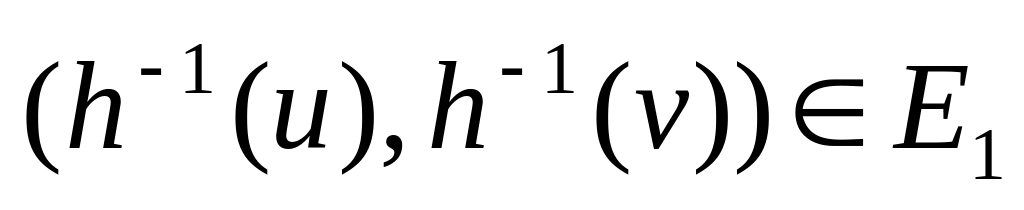 .
.
Изоморфизм графов есть отношение эквивалентности. Следовательно, множество всех графов разбивается на классы эквивалентности по отношению изоморфизма. Изоморфные графы принято отождествлять, т.е. считать одинаковыми.
Матрицы смежности и инцидентности
Пусть
– помеченный неориентированный граф
(возможно, мульти- или песевдограф)
порядка
.
Определим помеченную
![]() матрицу
матрицу
![]() ,
положив:
,
положив:
![]() ,
,
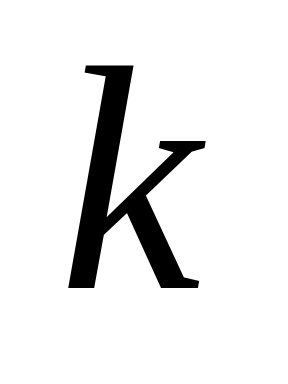 – число ребер
– число ребер
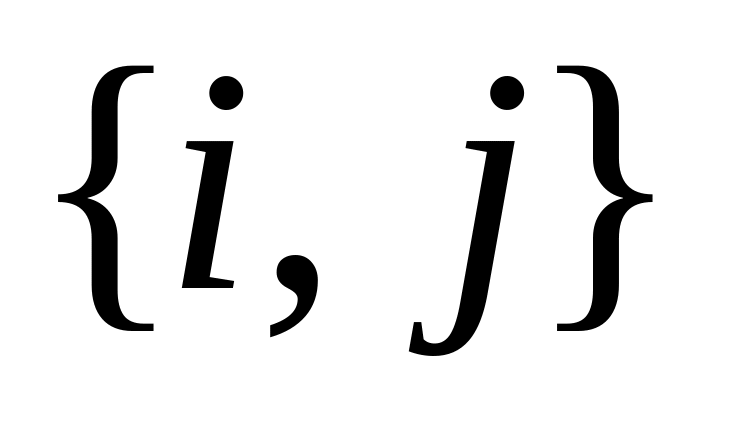 ,
при этом петля означает два ребра.
,
при этом петля означает два ребра.
![]() называется матрицей смежности графа
.
Это симметричная матрица.
называется матрицей смежности графа
.
Это симметричная матрица.
Матрица смежности орграфа:
![]() ,
,
– число дуг
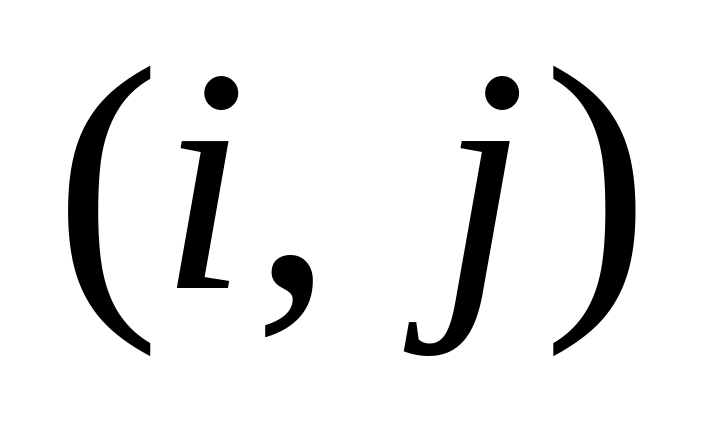 .
.
Пусть
–
неориентированный граф (возможно,
мульти- или песевдограф),
![]() ,
,
![]() .
Определим
.
Определим
![]() матрицу
матрицу
![]() :
:
 .
.
Матрица
![]() называется матрицей инцидентности
графа
.
называется матрицей инцидентности
графа
.
Пусть – ориентированный граф. Тогда матрица инцидентности определяется так:
 .
.
Элементы графов
Подграфы
Граф
 называется подграфом (или частью) графа
,
если
называется подграфом (или частью) графа
,
если
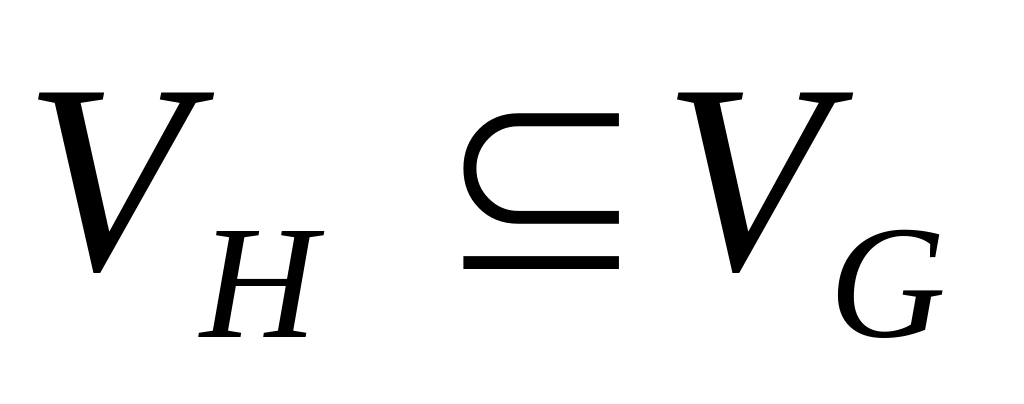 ,
,
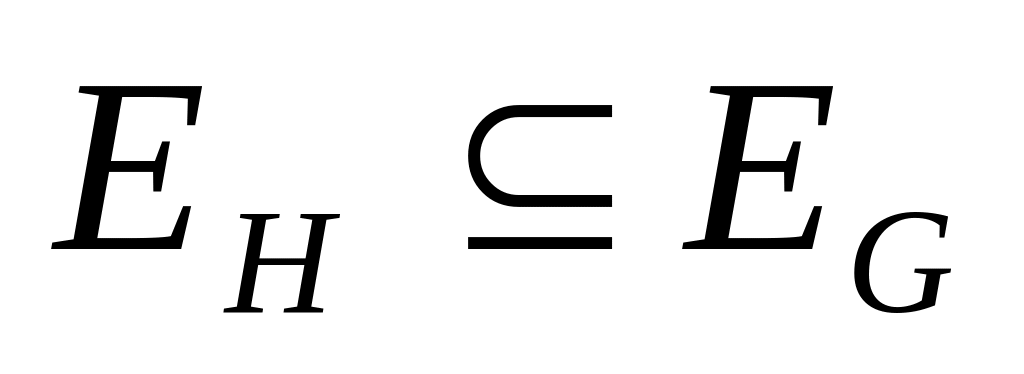 (при этом говорят, что
содержится в
).
(при этом говорят, что
содержится в
).
Подграф называется остовным подграфом, если
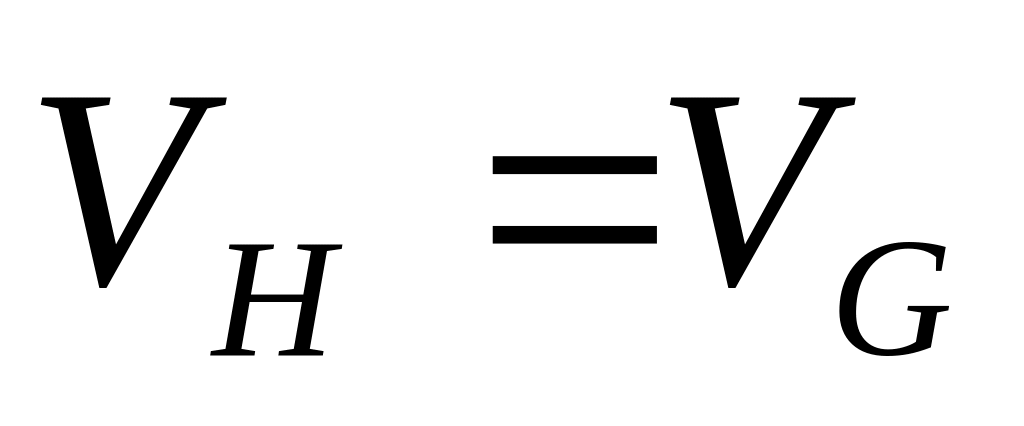 .
.
Важный класс подграфов составляют подграфы, полученные в результате удаления вершин. Пусть – вершина графа . Граф
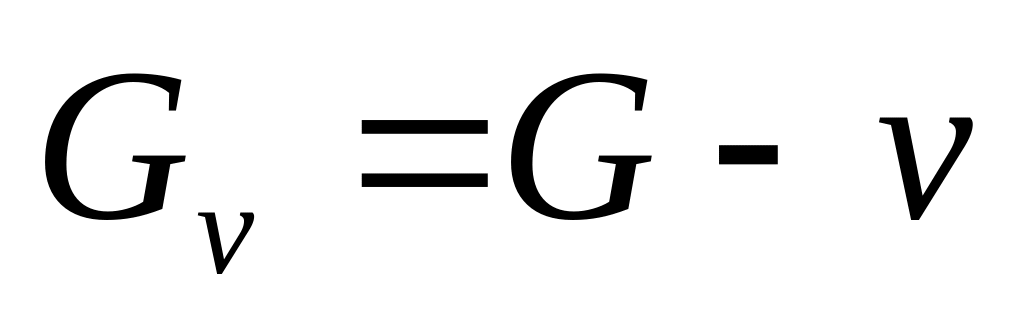 получается из графа
в результате удаления вершины
и всех инцидентных ей ребер.
получается из графа
в результате удаления вершины
и всех инцидентных ей ребер.Аналогично из графа можно удалять ребро. Граф
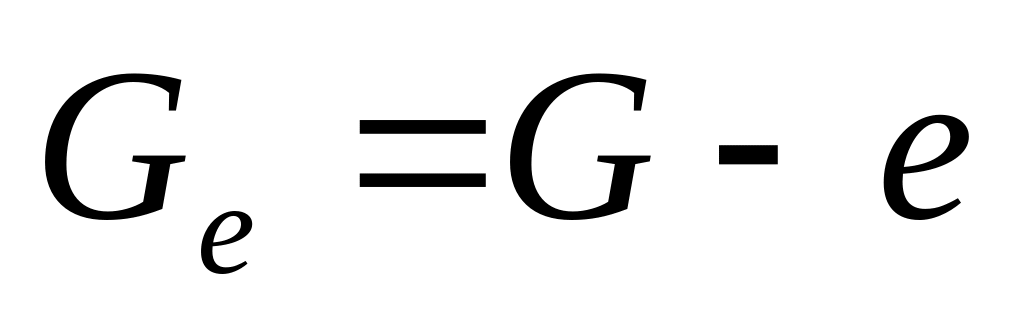 получается из графа
удалением ребра
,
при этом концы ребра не удаляются.
получается из графа
удалением ребра
,
при этом концы ребра не удаляются.Пусть
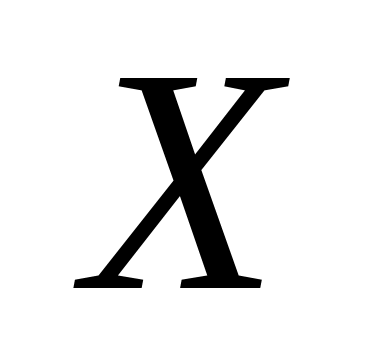 – множество каких-либо элементов
(вершин и ребер) графа
.
Подграф
– множество каких-либо элементов
(вершин и ребер) графа
.
Подграф
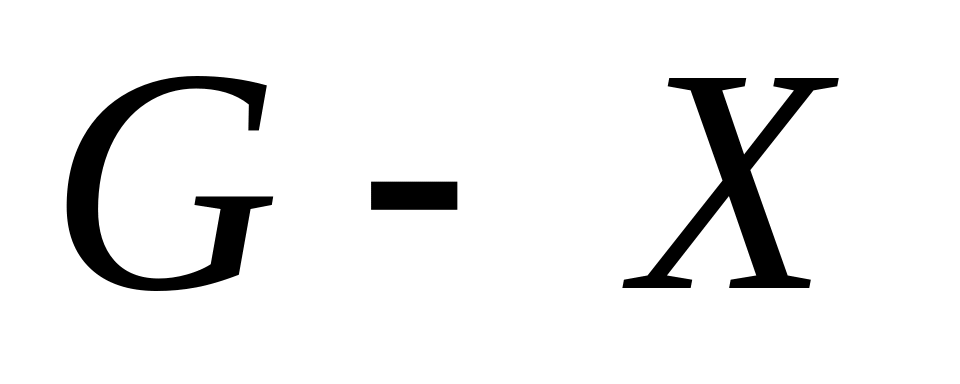 получается удалением из
всех вершин и ребер, входящих в
,
а также всех ребер, хотя бы один конец
которых принадлежит
.
получается удалением из
всех вершин и ребер, входящих в
,
а также всех ребер, хотя бы один конец
которых принадлежит
.
X={1,{2,3},4,{5,7}}
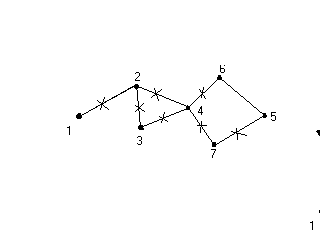
Степени вершин графа
Степенью (или валентностью) вершины графа называется число инцидентных ей ребер. Петля вносит в степень соответствующей вершины двойку. Будем обозначать степень вершины через
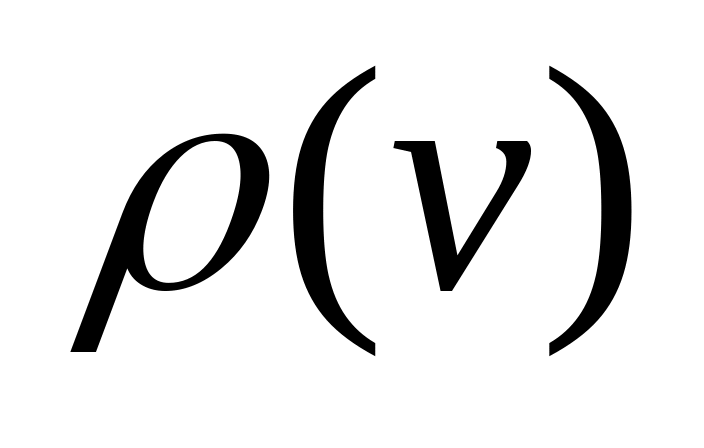 .
.
Максимальная и минимальная степени
вершин графа
обозначаются символами
![]() и
и
![]() соответственно:
соответственно:
![]() ,
,
![]() .
.
Список степеней вершин графа называется его степенной последовательностью. Порядок членов этой последовательности роли не играет.
Вершина степени 0 называется изолированной, вершина степени 1 – концевой (или висячей).
Рассмотрим сумму степеней всех вершин графа. Каждое ребро вносит в эту сумму двойку, поэтому справедлива следующая лемма.
(«лемма о рукопожатиях»). Сумма степеней всех вершин графа – четное число, равное удвоенному числу ребер:
![]() .
.
Для вершин ориентированного графа
определяются две локальные степени:
![]() – количество выходящих из
ребер, и
– количество выходящих из
ребер, и
![]() – количество входящих в вершину
ребер. Петля дает 1 в обе эти степени.
– количество входящих в вершину
ребер. Петля дает 1 в обе эти степени.
