- •Правила дифференцирования. Производные степенных, тригонометрических, показательных и логарифмических, сложных и обратной функций
- •Правила дифференцирования
- •Правила дифференцирования, доказательство и примеры.
- •Элементы множества.Основные понятия. Примеры множеств
- •Пример:
- •Свойство операций над множествами
- •Определения графов
- •Основные определения
- •Другие определения графов
- •Изоморфизм графов
- •Матрицы смежности и инцидентности
- •Элементы графов
- •Подграфы
- •Степени вершин графа
- •Маршруты, цепи, циклы
- •Связность
- •Связные графы. Компоненты связности
- •Вершинная и реберная связность
- •Двусвязные графы
- •Связность в орграфах
- •Метрические характеристики графа
- •Виды графов и операции над графами
- •Виды графов
- •Реберный граф
- •Операции над графами
- •1. Основные понятия теории вероятностей. Классическое, статистическое и геометрическое определения вероятности, свойства вероятности.
- •1)Основные понятия теории вероятностей.
- •5)Геометрическое определение вероятности.
- •1.4. Введение в логику высказываний Высказывания и операции над ними
- •[Править]Методы
- •[Править]Варианты округления 0,5 к ближайшему целому
- •[Править]Применения
- •[Править]Использование округлений при работе с числами ограниченной точности
- •[Править]Эмпирические правила арифметики с округлениями
Пример:
Дополнение к множеству квадратов в множестве ромбов является множество ромбов с хотя бы одним острым углом. А дополнение того же множества квадратов в множестве прямоугольников является множество прямоугольников с неравными соседними стороными.
Свойство операций над множествами
Справедливы следующие свойства операций над множествами:
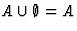 ,
где 0 -пустое множество.
,
где 0 -пустое множество.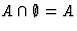 ,
где 0 - пустое множество.
,
где 0 - пустое множество.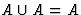
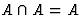
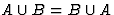

 ,
если
,
если 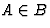
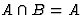 ,
если
,
если
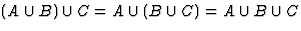
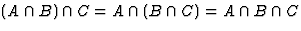
Графы
Теория графов неоднократно переоткрывалась разными авторами при решении различных прикладных задач.
1.Начало теории графов относят к 1736 г., когда Эйлер решил популярную в то время задачу о кенигсбергских мостах (сегодня Калининград). Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку.

2. Задача о трех домах и трех колодцах. Имеется 3 дома и 3 колодца. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались. Эта задача была решена Куратовским в 1930г.
Определения графов
Основные определения
Пусть
![]() - непустое конечное множество. Обозначим
через
- непустое конечное множество. Обозначим
через
![]() множество всех его двухэлементных
подмножеств (порядок элементов в
двухэлементных подмножествах не имеет
значения), т.е.
множество всех его двухэлементных
подмножеств (порядок элементов в
двухэлементных подмножествах не имеет
значения), т.е.
![]() .
.
Пара
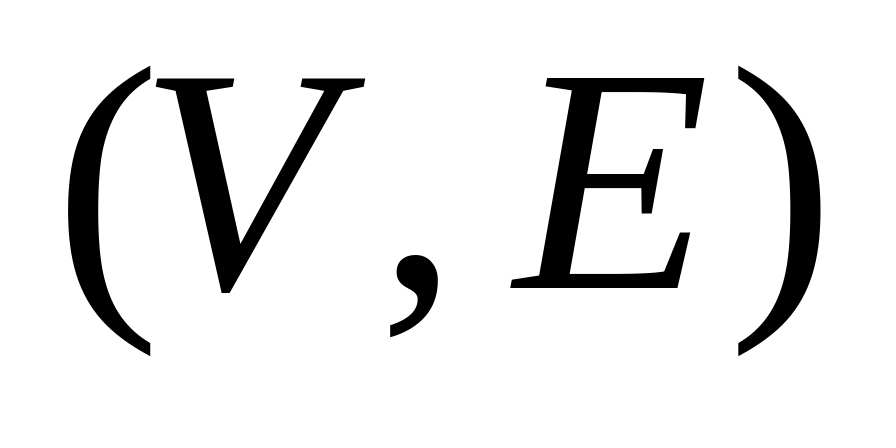 ,
где
,
где
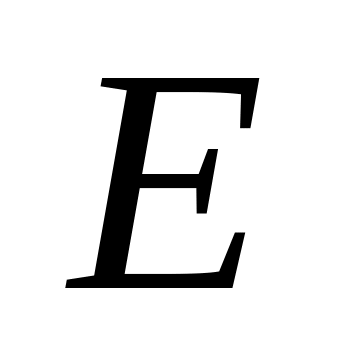 – произвольное подмножество
– произвольное подмножество
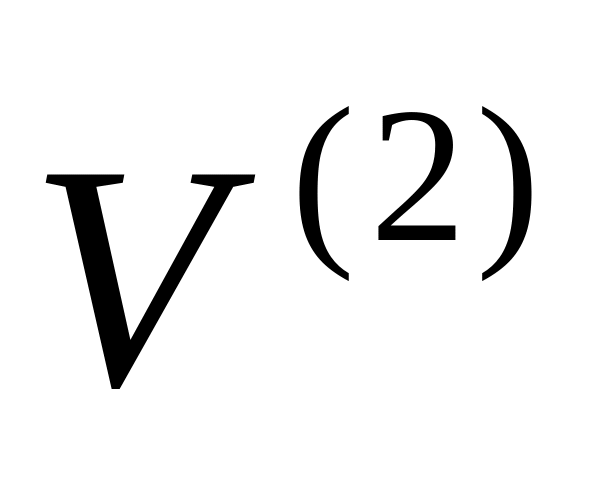 ,
называется графом (неориентированным
графом). Элементы множества
называются вершинами графа, а элементы
множества
– ребрами.
,
называется графом (неориентированным
графом). Элементы множества
называются вершинами графа, а элементы
множества
– ребрами.
Итак, граф – это конечное множество вершин и множество ребер.
Множества вершин и ребер графа
![]() будем соответственно обозначать
будем соответственно обозначать
![]() и
и
![]() .
Вершины и ребра графа называются его
элементами. Число вершин графа
называется его порядком и обозначается
.
Вершины и ребра графа называются его
элементами. Число вершин графа
называется его порядком и обозначается
![]() .
Если
.
Если
![]() ,
,
![]() ,
то граф
называют
,
то граф
называют
![]() –графом.
–графом.
Говорят, что две вершины
 и
и
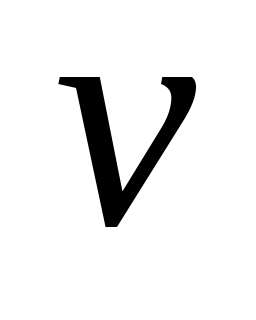 графа смежны, если множество
графа смежны, если множество
 является ребром, и не смежны в противном
случае.
является ребром, и не смежны в противном
случае.Если
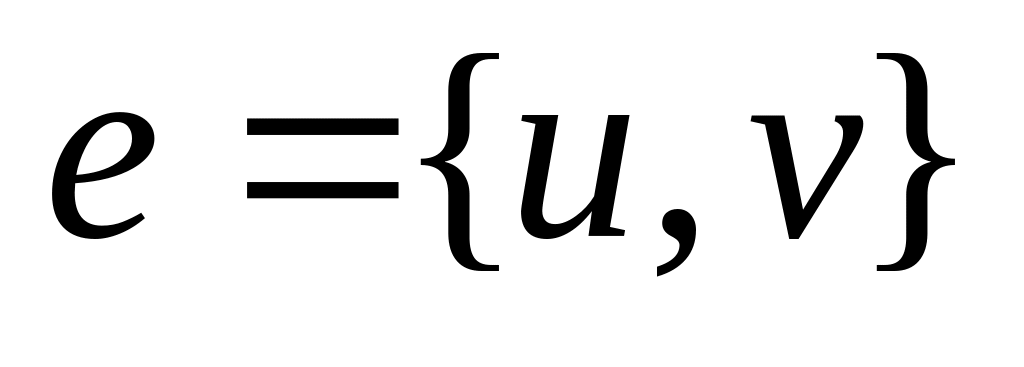 – ребро, то вершины
и
называют его концами.
– ребро, то вершины
и
называют его концами.Два ребра называются смежными, если они имеют общий конец.
Вершина и ребро
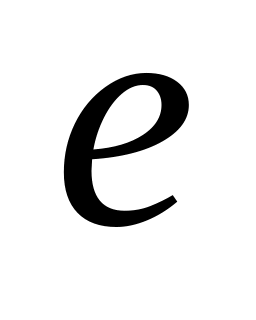 называются инцидентными, если
является концом ребра
.
называются инцидентными, если
является концом ребра
.Множество всех вершин графа , смежных с некоторой вершиной , называется окружением вершины и обозначается через
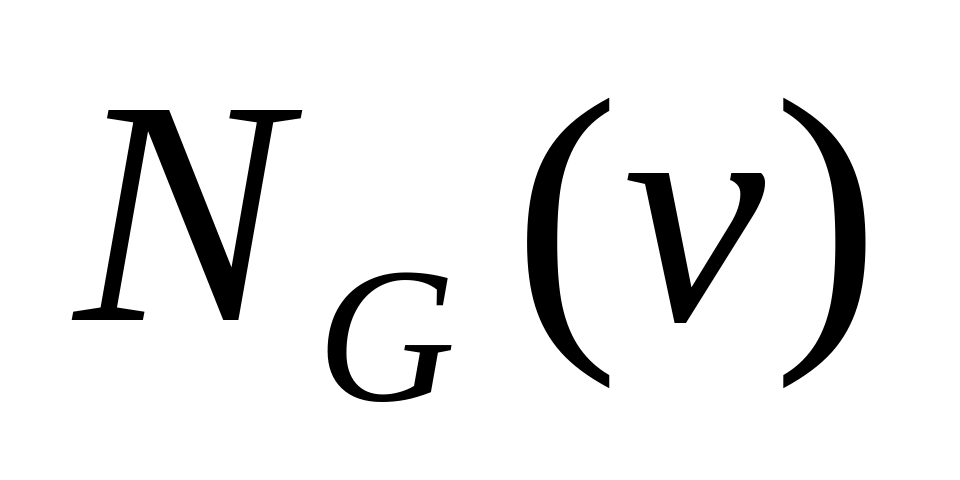 .
.Граф порядка
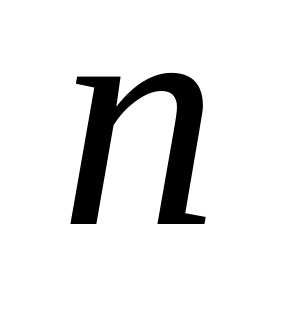 называется помеченным, если его вершинам
присвоены некоторые метки, например,
номера 1,2,3,…,
.
называется помеченным, если его вершинам
присвоены некоторые метки, например,
номера 1,2,3,…,
.
Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. При этом точки соответствуют вершинам графа, а соединяющие пары точек линии – ребрам.
Рассмотрим граф:
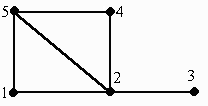
Это (5,6)–граф,
![]() ,
,
![]() .
Вершины 1 и 2 смежны, а 1 и 3 – не смежны.
Вершина 1 и ребро
.
Вершины 1 и 2 смежны, а 1 и 3 – не смежны.
Вершина 1 и ребро
![]() инцидентны,
инцидентны,
![]() .
.
Другие определения графов
Иногда приведенное выше определение графа оказывается недостаточным и приходится рассматривать более общие объекты, в которых вершины могут соединяться более, чем одним ребром. Так возникает понятие мультиграф.
Мультиграф – это пара , где – непустое множество вершин, а – комплект неупорядоченных пар вершин. То есть, в мультиграфе допускаются кратные ребра.
Мультиграф:

Дальнейшее обобщение состоит в том, что кроме кратных ребер допускаются еще петли, то есть ребра, соединяющие вершину саму с собой.
Псевдограф – это пара , где – непустое множество вершин, а – комплект неупорядоченных пар вершин, не обязательно различных.
Псевдограф:
Изучаются также ориентированные графы.
Тогда множество
заменяется декартовым произведением
![]() ,
состоящим из упорядоченных пар элементов
множества
.
,
состоящим из упорядоченных пар элементов
множества
.
Ориентированный граф (орграф) – это пара
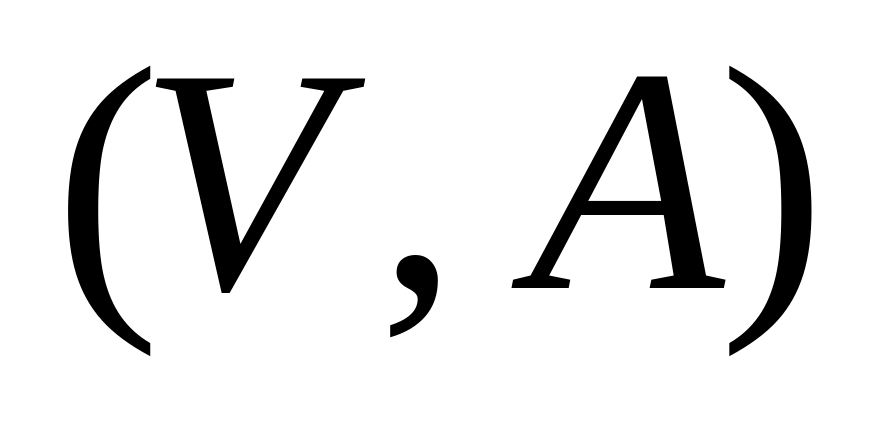 ,
где
– множество вершин,
,
где
– множество вершин,
 – множество ориентированных ребер,
которые называются дугами,
– множество ориентированных ребер,
которые называются дугами,
 .
.
Если
![]() – дуга, то вершина
– дуга, то вершина
![]() называется ее началом, а вершина
называется ее началом, а вершина
![]() – концом. На рисунке дуги обозначаются
стрелками, указывающими направление
от начала к концу.
– концом. На рисунке дуги обозначаются
стрелками, указывающими направление
от начала к концу.
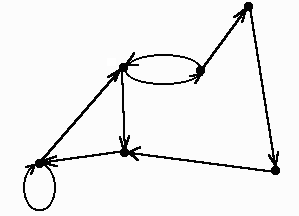
Орграф:

Аналогично определяются ориентированный мультиграф и псевдограф: