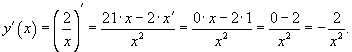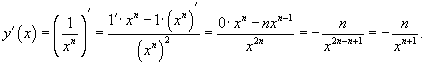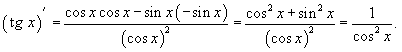- •Правила дифференцирования. Производные степенных, тригонометрических, показательных и логарифмических, сложных и обратной функций
- •Правила дифференцирования
- •Правила дифференцирования, доказательство и примеры.
- •Элементы множества.Основные понятия. Примеры множеств
- •Пример:
- •Свойство операций над множествами
- •Определения графов
- •Основные определения
- •Другие определения графов
- •Изоморфизм графов
- •Матрицы смежности и инцидентности
- •Элементы графов
- •Подграфы
- •Степени вершин графа
- •Маршруты, цепи, циклы
- •Связность
- •Связные графы. Компоненты связности
- •Вершинная и реберная связность
- •Двусвязные графы
- •Связность в орграфах
- •Метрические характеристики графа
- •Виды графов и операции над графами
- •Виды графов
- •Реберный граф
- •Операции над графами
- •1. Основные понятия теории вероятностей. Классическое, статистическое и геометрическое определения вероятности, свойства вероятности.
- •1)Основные понятия теории вероятностей.
- •5)Геометрическое определение вероятности.
- •1.4. Введение в логику высказываний Высказывания и операции над ними
- •[Править]Методы
- •[Править]Варианты округления 0,5 к ближайшему целому
- •[Править]Применения
- •[Править]Использование округлений при работе с числами ограниченной точности
- •[Править]Эмпирические правила арифметики с округлениями
Производная произведения и частного функций |
|
Производная произведения функций. Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и
Внимание: Производная произведения двух функций НЕ РАВНА произведению производных этих функций! Производная частного функций. Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле
|
Пример 1 |
|
Найти производную
функции Решение. Используем правило для вычисления производной частного. |
Пример 2 |
|
Найти производную
cтепенной функции с отрицательным
показателем Решение. Запишем
функцию в виде |
Пример 3 |
|
Вычислить производную y(x) = tg x используя формулу производного частного. Решение. Запишем
тангенс в виде Поскольку |
Пример 4 |
|
Пусть Решение. Представим функцию в виде y(x) = sinxsinx. По формуле производной произведения Так как , получаем
|
Пример 5 |
|
Найти формулу для производной произведения трех функций. Решение. Пусть Поскольку |
Правила дифференцирования. Производные степенных, тригонометрических, показательных и логарифмических, сложных и обратной функций

Производные степенных и тригонометрических функций.
Основные формулы:

Производная сложной функции.

Производные показательных и логарифмических функций.
Основные формулы:
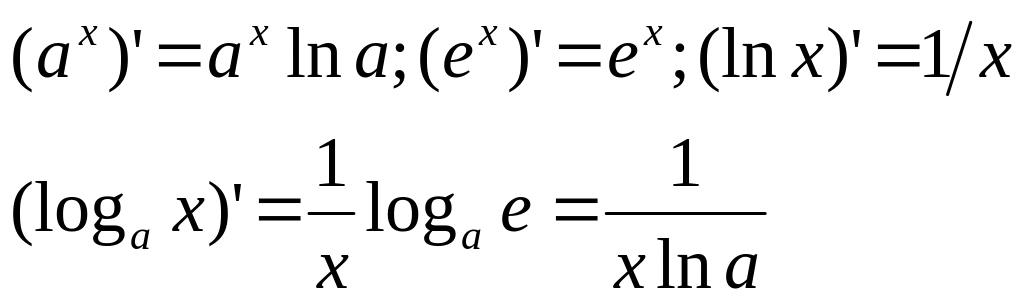
Если z=z(x) – дифференцируемая функция от x, то формулы имеют вид:

Производные обратных тригонометрических функций.
Основные формулы:

Для сложных функций:

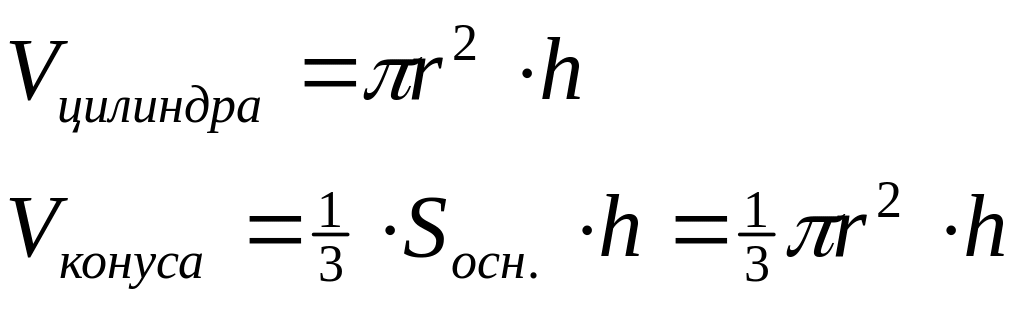
Правила дифференцирования
При
дифференцировании константу можно
выносить за производную:
![]() Правило
дифференцирования суммы функций:
Правило
дифференцирования суммы функций:
![]() Правило
дифференцирования разности
функций:
Правило
дифференцирования разности
функций:
![]() Правило
дифференцирования произведения функций
(правило Лейбница):
Правило
дифференцирования произведения функций
(правило Лейбница):
![]() Правило
дифференцирования частного
функций:
Правило
дифференцирования частного
функций:
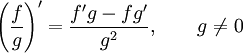 Правило
дифференцирования функции в степени
другой функции:
Правило
дифференцирования функции в степени
другой функции:
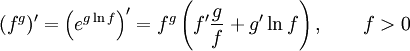 Правило
дифференцирования сложной
функции:
Правило
дифференцирования сложной
функции:
![]() Правило
логарифма при дифференцировании
функции:
Правило
логарифма при дифференцировании
функции:
![]()
Правила дифференцирования, доказательство и примеры.
При решении задач дифференцирования приходится искать производные функций различных классов. В этой статье мы рассмотрим основные правила дифференцирования, которые будем постоянно использовать при нахождении производных. Все эти правила докажем на основе определения производной функции и обязательно остановимся на подробном решении примеров, чтобы понять принцип их применения.
При доказательстве правил дифференцирования будем считать функции f(x) и g(x)дифференцируемыми на некотором промежутке X.
То
есть, для любого ![]() справедливо
справедливо ![]() ,
где
,
где ![]() -
приращения соответствующих функций.
-
приращения соответствующих функций.
В
другой записи ![]() .
.
К основным правилам дифференцирования относят:
вынесение постоянного множителя за знак производной
производная суммы, производная разности
производная произведения функций
производная частного двух функций (производная дроби)
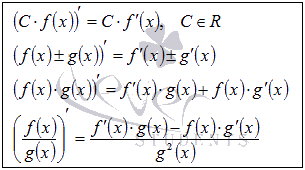
Вынесение постоянного множителя за знак производной.
Докажем
формулу ![]() .
По определению производной имеем:
.
По определению производной имеем:

Произвольный
множитель можно выносить за знак
предельного перехода (это известно из
свойств предела), поэтому
![]()
На этом доказательство первого правила дифференцирования завершено.
Пример.
Найти
производную функции ![]() .
.
Решение.
Из таблицы
производных для
тригонометрических функций видим ![]() .
Воспользуемся правилом вынесения
множителя за знак производной:
.
Воспользуемся правилом вынесения
множителя за знак производной:
![]()
Достаточно часто приходится сначала упрощать вид дифференцируемой функции, чтобы воспользоваться таблицей производных и правилами нахождения производных. Следующие примеры это наглядно подтверждают.
Пример.
Выполнить
дифференцирование функции ![]() .
.
Решение.
По
свойствам логарифмической функции
можно перейти к записи ![]() .
Осталось вспомнить производную
логарифмической функции и вынести
постоянный множитель:
.
Осталось вспомнить производную
логарифмической функции и вынести
постоянный множитель:
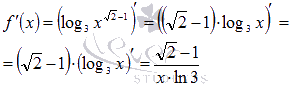
Пример.
Найти
производную функции 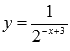 .
.
Решение.
Преобразуем
исходную функцию  .
.
Применяем
правило вынесения множителя за знак
производной и из таблицы берем производную
показательной функции:
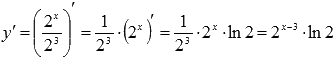
Основные понятия Неопределенного интеграла
Примеры решений задач
Решить неопределенный интеграл
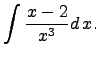
ответ и решение
Решить неопределенный интеграл
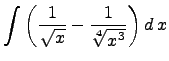
ответ и решение
Решить неопределенный интеграл

ответ и решение
Дадим строгое математическое определение понятия неопределенного интеграла.
Выражение
вида ![]() называется интегралом
от функции f(x),
где f(x) -
подынтегральная функция, которая
задается (известная), dx -
дифференциал x,
с символом
называется интегралом
от функции f(x),
где f(x) -
подынтегральная функция, которая
задается (известная), dx -
дифференциал x,
с символом ![]() всегда
присутствует dx.
всегда
присутствует dx.
Определение. Неопределенным
интегралом
называется
функция F(x)
+ C,
содержащая произвольное постоянное C,
дифференциал которой
равенподынтегральному выражению f(x)dx,
т.е.![]() или
или ![]() Функцию
Функцию ![]() называют первообразной
функции
называют первообразной
функции ![]() .
Первообразная функции
определяется
с точностью до постоянной величины.
.
Первообразная функции
определяется
с точностью до постоянной величины.
Напомним,
что ![]() -дифференциал
функции
и
определяется следующим образом:
-дифференциал
функции
и
определяется следующим образом:
![]()
Задача нахождения неопределенного интеграла заключается в нахождении такой функции,производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю.
Например,
известно, что ![]() ,
тогда получается, что
,
тогда получается, что ![]() ,
здесь
,
здесь ![]() -
произвольная постоянная.
-
произвольная постоянная.
Задача нахождение неопределенного интеграла от функций не столь простая и легкая, как кажется на первый взгляд. Во многих случаях должен быть навык работы снеопределенными интегралами, должен быть опыт, который приходит с практикой и с постоянным решением примеров на неопределенные интегралы. Стоит учитывать тот факт, что неопределенные интегралы от некоторых функций (их достаточно много) не берутся в элементарных функциях.