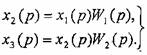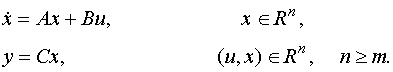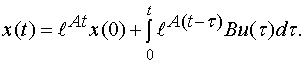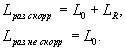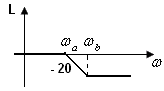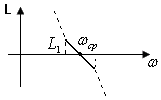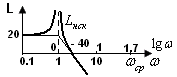- •3. Апериодическое (инерционное) звено или звено 1-го порядка.
- •Организационные вопросы
- •Лабораторная работа № 1
- •1. Цель работы
- •2. Основные сведения
- •3.Методические указания
- •4.Порядок выполнения работы
- •5.Содержание отчёта
- •6.Контрольные вопросы
- •3. Методические указания
- •4. Порядок выполнения работы
- •5. Содержание отчета
- •6. Контрольные вопросы
- •3. Методические указания
- •4. Порядок выполнения работы
- •5.Содержание отчета
- •6.Контрольные вопросы
- •3. Методические указания
- •4.Порядок выполнения работы
- •5.Содержание отчета
- •6.Контрольные вопросы
- •3. Методические указания
- •4. Порядок выполнения работы
- •5. Содержание отчета
- •6. Контрольные вопросы
- •3.Методические указания
- •4.Порядок выполнения работы
- •5.Содержание отчета
- •6.Контрольные вопросы
- •Задачи к экзамену по дисциплине Основы Теории Управления
Основы теории управления
Введение
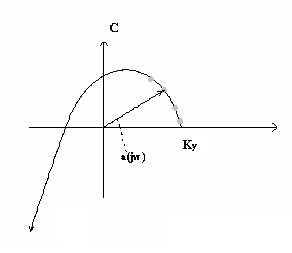
Сигналы управления и возмущения в общем случае могут быть не детерминированные, а случайные, поэтому приходиться прибегать к статистическим методам исследования систем автоматического управления (САУ). Кроме того, часть объектов функционирует и работает в конфликтных ситуациях. Рассмотрим график изменения выходного вектора САУ во времени (рис.2.)
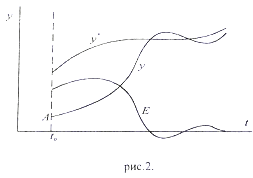
где у* — желаемая траектория объекта управления. В начальный момент гп система находилась в точке А. При включении системы управления выходная координата у под действием управляющих сигналов выходит на требуемую (желаемую) траекторию у*. Разность E(t)=y*(t)-y(t) называется ошибкой или рассогласованием САУ. задача теории автоматического управления (ТАУ) состоит:
Научиться проектировать системы управления, обеспечивающие минимальные допустимые для данного объекта ошибки E(t);
проектировать системы управления, которые обеспечивают выход системы на желаемую траекторию за минимальное время, т.е. решается задача быстродействия соответствующим выбором системы управления.
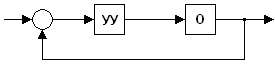
Итак, в самом общем случае САУ, выполняющая поставленные выше задачи, может быть представлена в виде блок-схемы (рис.З)
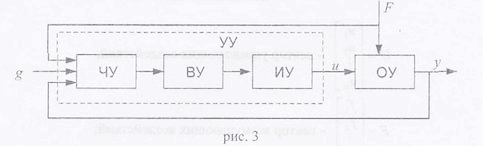
На вход управляющего устройства (УУ) поступает:
задающее воздействие g;
информация о текущем состоянии объекта в виде выходной величины у;
информация о действующем на ОУ возмущении F.
УУ вырабатывает, в соответствии с полученной информацией, определенное (по заданному алгоритму) управляющее воздействие и на объект. В свою очередь УУ в общем случае состоит из:
- чувствительного устройства (ЧУ); - вычислительного устройства (ВУ); - исполнительного устройства (ИУ).
Чувствительное устройство (измерительные устройства, датчики) служат для измерения и преобразования подаваемых на УУ воздействий g, у, F. Вычислительное устройство реализует алгоритм работы УУ. В простейших случаях оно осуществляет простые математические операции, такие как сравнения, т.е. разность g-y-F, операции интегрирования и т.п. В более сложных случаях вычислительное устройство может представлять собой ЭВМ, и даже комплекс ЭВМ. Исполнительные устройства предназначены для непосредственного управления ОУ. Например, для согласования мощности ВУ и ОУ необходимо применить усилитель мощности. В тех случаях, когда ИУ отсутствует, САУ называется прямого регулирования. При наличии ИУ САУ называется непрямого регулирования.
Лекция №2
Математическое описание автоматической системы управления.
Дифференциальное уравнение.
 Система
или устройство x(t)-вход, y(t)- выход. В
большинстве случаев при описании
используется дифференциальное уравнение.
Правая часть содержит производные
входа, левая часть производные выхода.
Система
или устройство x(t)-вход, y(t)- выход. В
большинстве случаев при описании
используется дифференциальное уравнение.
Правая часть содержит производные
входа, левая часть производные выхода.
![]()
m, n – порядок управления, чаще всего так говорят про число n.
![]()
Пример
1.
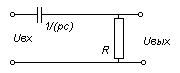
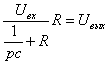
![]()
![]()
![]()
Операторное представление.
![]()
![]()
![]()
![]()
Преобразования
Лапласа.
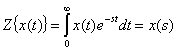
![]()
![]() -
оригинал.
-
оригинал.
![]() -
изображение.
Применим преобразования
Лапласа к заданному дифференциальному
уравнению при нулевых начальных условиях,
в результате получим.
-
изображение.
Применим преобразования
Лапласа к заданному дифференциальному
уравнению при нулевых начальных условиях,
в результате получим.
![]() s-
комплексная переменная
x,y-функции
от s.
s-
комплексная переменная
x,y-функции
от s.
Передаточная функция(коэффициент передачи).
Отношение
изображения выходного сигнала к
изображению входного сигала, при нулевых
начальных условиях, называется
передаточной функцией. Пусть объект
описывается уравнением, применим к нему
преобразования Лапласа.
![]()
![]()
![]() -
передаточная функция.
Пример:
-
передаточная функция.
Пример:
![]() Найти
коэффициент передачи.
Найти
коэффициент передачи.
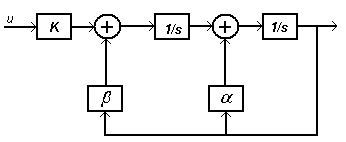
![]() Моделирование
динамических объектов(систем).
Моделирование
динамических объектов(систем).
![]()
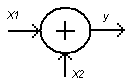
![]() найти
решение -->
найти
решение --> ![]() Утверждение:
Системы уравнений могут быть смоделированы
при помощи трех функциональных
блоков.
Утверждение:
Системы уравнений могут быть смоделированы
при помощи трех функциональных
блоков.
 -сумматор
-сумматор
 -усилитель
-усилитель
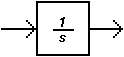 –интегратор
Пример:
–интегратор
Пример:
![]() Смоделировать
устройство которое описывается этим
уравнением.
Переходим к
изображению
Смоделировать
устройство которое описывается этим
уравнением.
Переходим к
изображению
![]()
![]()
![]()
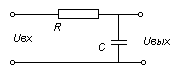
![]() Принципиальная
схема:
Принципиальная
схема:
Лекция №3
Характеристики динамических систем:
Временные.
Частотные.
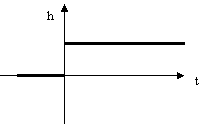
Временное
устройство
U(t)=1 или u(t)=1(t) – на вход
подается единичный сигнал.
выходной
сигнал h(t) – переходной функцией
называется реакция на единичную
ступень.
Если перейти к
изображению.
y(s)=w(s)u(s)
![]() s-комплексная
переменная.
s-комплексная
переменная.
![]() -
изображение переходной функции равно
изображению передаточной функции
деленное на s.
Импульсная переходная
функция(весовая функция).
Называется
реакция системы на импульс.
-
изображение переходной функции равно
изображению передаточной функции
деленное на s.
Импульсная переходная
функция(весовая функция).
Называется
реакция системы на импульс.
![]() -
реакция системы на импульс.
-
реакция системы на импульс.
![]() -
дельта импульс.
-
дельта импульс.
![]()
![]()
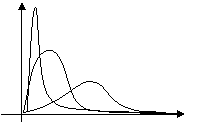 Основная
характеристика дельта импульса:
Основная
характеристика дельта импульса:
 высота
дельта импульса стремиться к
высота
дельта импульса стремиться к ![]() ширина
дельта импульса стремиться к
0
S=1
Рассмотрим связь между двумя
временными характеристиками и их
изображением.
ширина
дельта импульса стремиться к
0
S=1
Рассмотрим связь между двумя
временными характеристиками и их
изображением.
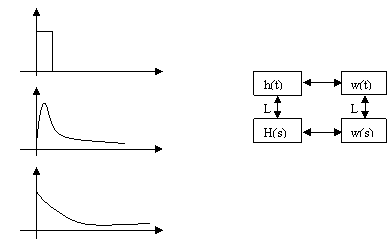 Пример:
Апериодическое
звено.
Пример:
Апериодическое
звено.
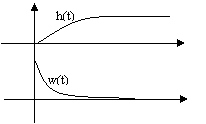
![]() -
связь между изображением переходной
функции и изображением импульсной
переходной функцией.
Интеграл от
импульсной переходной функции есть
переходная функция. Реальное
дифференцирующее звено.
-
связь между изображением переходной
функции и изображением импульсной
переходной функцией.
Интеграл от
импульсной переходной функции есть
переходная функция. Реальное
дифференцирующее звено. 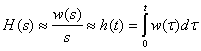
![]()
![]()
![]()
![]()
![]()
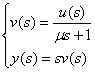
Лекция №4
При
исследовании и создании САУ, аппарат
частотных характеристик был одним из
первых, т.к они наиболее полно отражают
физическую природу процессов, происходящих
в динамических объектах.
В качестве
преобразования функции f(t) используется
преобразование Фурье
![]() Преобразование
Фурье позволяет разложить непериодическую
функцию f(t) для
которой выполняется условие сходимости
Преобразование
Фурье позволяет разложить непериодическую
функцию f(t) для
которой выполняется условие сходимости
![]() в
бесконечный ряд гармоник, образующих
непрерывный спектр частот в интервале
в
бесконечный ряд гармоник, образующих
непрерывный спектр частот в интервале ![]() от
до
от
до![]() с
бесконечно малым интервалом частот
между смежными частотами (
с
бесконечно малым интервалом частот
между смежными частотами (![]() 0).
Отметим,
что по сравнению с преобразованием
Лапласа преобразование Фурье позволяет
отобразить оригинал только на мнимую
ось, в преобразовании Лапласа же
используется вся комплексная плоскость.
Для
перехода к частотным
характеристикам, необходимо в уравнение
ПФ (3) вместо оператора Лапласа p подставить
оператор Фурье
0).
Отметим,
что по сравнению с преобразованием
Лапласа преобразование Фурье позволяет
отобразить оригинал только на мнимую
ось, в преобразовании Лапласа же
используется вся комплексная плоскость.
Для
перехода к частотным
характеристикам, необходимо в уравнение
ПФ (3) вместо оператора Лапласа p подставить
оператор Фурье ![]() ,
получим частотную характеристику
,
получим частотную характеристику
|
(3) |
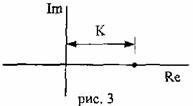
Рассмотрим понятие о частотных характеристиках. Если на вход линейной разомкнутой системы (или звена) подать гармонический входной сигнал, то по истечении некоторого времени окончания переходных процессов на выходе системы (звена) установится также гармонический выходной сигнал той же частоты. Амплитуда и фаза при прочих равных условиях будут зависеть от частоты входного сигнала. По ним, как будет показано дальше, можно судить о свойствах САУ.
Достоинством
частотных методов является то, что
частотные характеристики можно снять
экспериментально. Чтобы снять частотную
характеристику необходимо на вход
подавать гармонический сигнал, изменяя
частоту от 0 до
,
а на выходе измерять амплитуду и фазу
для частот wi,.
Отметим
еще, что в выражении передаточной функции
и частотной характеристики для реальных
систем степень знаменателя всегда
больше степени числителя n>m,
т.к. полоса пропускания частот реальной
системы всегда ограничена. Действительно,
если n<m,
то на выходе системы при увеличении
частоты могут возникнуть колебания с
бесконечно большой амплитудой.
Частотная
характеристика (ЧХ) элемента или
системы![]() может
быть представлена в двух видах:
может
быть представлена в двух видах:
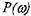 -
вещественно-частотная характеристика
(ВЧХ);
-
вещественно-частотная характеристика
(ВЧХ);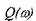 -
мнимо-частотная характеристика (МЧХ);
-
мнимо-частотная характеристика (МЧХ);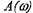 -
амплитудно-частотная характеристика
(АЧХ);
-
амплитудно-частотная характеристика
(АЧХ); -
фазо-частотная характеристика (ФЧХ).
-
фазо-частотная характеристика (ФЧХ).
Часто ЧХ представляется графически (рис.1) на комплексной плоскости, где все указанные величины связаны между собой по следующим соотношениям.

![]()
![]()
Часто при исследовании систем используются логарифмические частотные характеристики.
Понятие о логарифмических частотных характеристиках
При исследовании САУ, амплитудную и фазовую частотные характеристики удобно строить в логарифмических координатах. Это связано с двумя обстоятельствами:
в логарифмических масштабах кривизна характеристик резко уменьшается, что позволяет в большинстве практических случаев приближенно изображать АЧХ ломаными линиями
в логарифмических масштабах АЧХ цепочки звеньев равна сумме АЧХ отдельных звеньев
![]()
АЧХ
в логарифмических масштабах строится
в координатах![]() и
и![]() а
ФЧХ - в виде зависимости
а
ФЧХ - в виде зависимости![]() от
от![]() .
Единицей измерения
.
Единицей измерения ![]() служит
децибел, равная 0,1 бела. Бел - единица
измерения десятичного логарифма
коэффициента усиления мощности сигнала,
т.е. 1 бел соответствует усилению мощности
в 10 раз, 2 бела - в 100 раз и т.д. Так как
мощность сигнала пропорциональна
квадрату амплитуды А2
(Пример:
для электрической цепи
служит
децибел, равная 0,1 бела. Бел - единица
измерения десятичного логарифма
коэффициента усиления мощности сигнала,
т.е. 1 бел соответствует усилению мощности
в 10 раз, 2 бела - в 100 раз и т.д. Так как
мощность сигнала пропорциональна
квадрату амплитуды А2
(Пример:
для электрической цепи![]() ).
).![]() ,
то усиление в белах, выраженное через
отношение амплитуд A, равно
,
то усиление в белах, выраженное через
отношение амплитуд A, равно ![]() ,
соответственно в децибелах оно равно
,
соответственно в децибелах оно равно
![]()
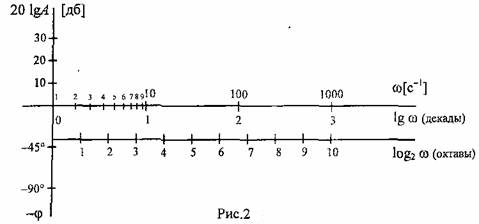
По
оси абсцисс откладывается в логарифмическом
масштабе частот ![]() (десятичный
логарифм)(изменение частоты в 10 раз -
декада), а около отметок указывается
само значение частоты. Иногда По оси
абсцисс откладывается в логарифмическом
масштабе частота
(десятичный
логарифм) (изменение частоты в 10 раз -
декада), а около отметок указывается
само значение частоты. Иногда применяется
логарифм частоты при основании 2
(изменение частоты в два раза - октава)
одна октава разно 0,303 декады, т.к. lg2 =
0,303 .
(десятичный
логарифм)(изменение частоты в 10 раз -
декада), а около отметок указывается
само значение частоты. Иногда По оси
абсцисс откладывается в логарифмическом
масштабе частота
(десятичный
логарифм) (изменение частоты в 10 раз -
декада), а около отметок указывается
само значение частоты. Иногда применяется
логарифм частоты при основании 2
(изменение частоты в два раза - октава)
одна октава разно 0,303 декады, т.к. lg2 =
0,303 .
Для
построения логарифмических фазовых
характеристик (ЛФХ) на оси абсцисс
используется аналогичная шкала
частот ![]() или
или ![]() ,
а по оси ординат (обычно используется
нижняя часть плоскости) откладывается
фаза в градусах.
,
а по оси ординат (обычно используется
нижняя часть плоскости) откладывается
фаза в градусах.
Отметим
ещё, т.к. точка ![]() =0 в
логарифмическом масштабе находится
слева , то ЛАФХ строятся не от
=0,
а от достаточно малого, но конечного
значения
,
которое и откладывается в начале
координат
=0 в
логарифмическом масштабе находится
слева , то ЛАФХ строятся не от
=0,
а от достаточно малого, но конечного
значения
,
которое и откладывается в начале
координат
Лекция №5
Усиливающее звено.
1.
Безынерционное звено, сигнал на выходе
которого, строго пропорционален сигналу
на входе, называется усилительным звеном
(рис.1).
 По
определению
По
определению![]() g(t) -
входное воздействие (один из стандартных
сигналов),
x(t) -реакция
на выходе, коэффициент пропорциональности.
g(t) -
входное воздействие (один из стандартных
сигналов),
x(t) -реакция
на выходе, коэффициент пропорциональности.
2.Переходя
к преобразованию Лапласа![]() ,
тогда передаточная функция:
к -
коэффициент усиления (если
величинабезразмерная) и коэффициент
передачи (если 6 размерно).
,
тогда передаточная функция:
к -
коэффициент усиления (если
величинабезразмерная) и коэффициент
передачи (если 6 размерно).
![]() 3.1.
Если на вход усилительного звена подать
единичную ступенчатую функцию g(t),
то переходная функция будет иметь вид,
как показано на рис.2.
3.1.
Если на вход усилительного звена подать
единичную ступенчатую функцию g(t),
то переходная функция будет иметь вид,
как показано на рис.2.
 3.2.
Для получения импульсной переходной
функции необходимо продифференцировать
по времени переходную характеристику,
тогда на выходе имеем
3.2.
Для получения импульсной переходной
функции необходимо продифференцировать
по времени переходную характеристику,
тогда на выходе имеем ![]() -функцию.
3.3.
Частотная характеристика
-функцию.
3.3.
Частотная характеристика ![]() 3.3.1.
3.3.1.
![]() на
комплексной плоскости имеет вид:
на
комплексной плоскости имеет вид:
 3.3.2.
ЛЧХ:
3.3.2.
ЛЧХ:
![]()
 ЛФХ:
ЛФХ:![]() Описание
реальных элементов динамическими
характеристиками усилительного
безинерционного звена является всегда
некоторой идеализацией, т.к. все реальные
объекты в природе - инерционны.
Описание
реальных элементов динамическими
характеристиками усилительного
безинерционного звена является всегда
некоторой идеализацией, т.к. все реальные
объекты в природе - инерционны.
Интегрирующее звено.
Звено
сигнал на выходе которго пропорционален
интегралу сигнала на выходе называется
интегрирующим звеном.
По
определению:
![]()
 2.
Из
2.
Из ![]() свойства
преобразования Лапласа:
Тогда по
определению передаточная функция
будет
свойства
преобразования Лапласа:
Тогда по
определению передаточная функция
будет
![]() Отметим,
что коэффициент передачи интегрирующего
эвена имеет размерность 1/сек.
3.1.
Если
Отметим,
что коэффициент передачи интегрирующего
эвена имеет размерность 1/сек.
3.1.
Если ![]() -
единичная ступенчатая функция, то
переходная функция интегрирующего
звена имеет вид (рис.6).
-
единичная ступенчатая функция, то
переходная функция интегрирующего
звена имеет вид (рис.6). 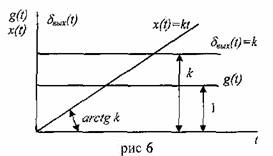 3.2.
Если
3.2.
Если ![]() ,
то, дифференцируя
,
то, дифференцируя![]() ,получим
,получим![]() (рис.6).
3.3.
Частотная характеристика.
3.3.1.
(рис.6).
3.3.
Частотная характеристика.
3.3.1. ![]()
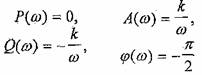 т.е.
амплитудно-фазовая характеристика при
изменении частоты от 0 до «э проходит
по отрицательной мнимой оси комплексной
плоскости (рис.7).
т.е.
амплитудно-фазовая характеристика при
изменении частоты от 0 до «э проходит
по отрицательной мнимой оси комплексной
плоскости (рис.7).
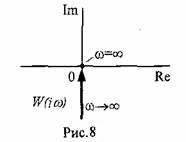 33.2.
ЛАХ:
33.2.
ЛАХ:![]() Вычислим
значение ЛАХ при
Вычислим
значение ЛАХ при![]() и
и![]()
![]() Следовательно,
при изменении частоты на 1 декаду,
амплитуда уменьшается на 20 децибел
(рис.8).
Следовательно,
при изменении частоты на 1 декаду,
амплитуда уменьшается на 20 децибел
(рис.8).
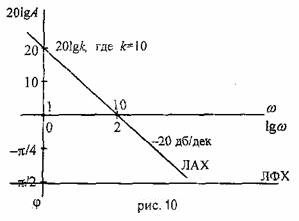 ЛФХ:
ЛФХ:![]()
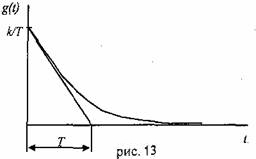
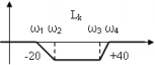
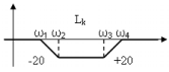
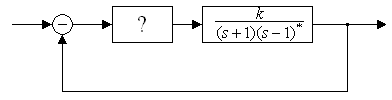
3. Апериодическое (инерционное) звено или звено 1-го порядка.
Звено,
которое описывается уравнением вида:
где
t - коэффициент передачи (усиления),
![]() Т
- постоянная времени, характеризующая
инерционность (с), называется апериодическим
звеном.
2. Переходя к преобразованию
Лапласа
Т
- постоянная времени, характеризующая
инерционность (с), называется апериодическим
звеном.
2. Переходя к преобразованию
Лапласа
|
(1) |
получим по определению передаточную функцию
|
(2) |
3.1
Переходная характеристика такого звена
при ![]() представляет
собой экспоненту
представляет
собой экспоненту
![]() Переходный
процесс достигает своего установившегося
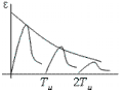
значения 0,95% практически за ЗГ (рис
12).
Переходный
процесс достигает своего установившегося
значения 0,95% практически за ЗГ (рис
12).
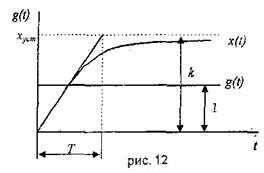 3.2
Импульсная переходная функция
при
3.2
Импульсная переходная функция
при![]() находится
дифференцированием
находится
дифференцированием![]() при
при ![]() =1,
получим
=1,
получим
![]() Если
эти характеристики получены
экспериментально, то по ним МОЖНО
определить Ги &, как показано на рис.
33 и 34. и, таким образом, получить уравнение
звена (что очень важно).
3.3.1
Частотная характеристика:
Если
эти характеристики получены
экспериментально, то по ним МОЖНО
определить Ги &, как показано на рис.
33 и 34. и, таким образом, получить уравнение
звена (что очень важно).
3.3.1
Частотная характеристика:
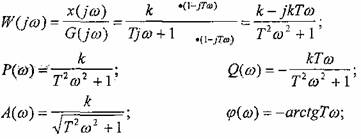 График
ЧХ в обычном масштабе (рис.35).
График
ЧХ в обычном масштабе (рис.35).
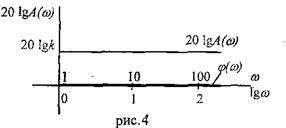
 3.3%
ЛАХ:
3.3%
ЛАХ: ![]() При k=1
При k=1 ![]() Построение:
Построение:
При малых частотах, где
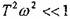 ,
пренебрегаем
,
пренебрегаем 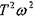 -
0.
-
0.
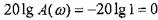
При больших частотах, где
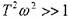 ,
пренебрегаем 1, тогда
,
пренебрегаем 1, тогда

В
области средних частот![]() ,
отсюда определяем частоту сопряжения
низкочастотной и высокочастотном
составляющей:
,
отсюда определяем частоту сопряжения
низкочастотной и высокочастотном
составляющей: ![]()
 Определим
наклон высокочастотное составляющей,
для чего вычислим изменение
Определим
наклон высокочастотное составляющей,
для чего вычислим изменение![]() при
изменении частоты в 10 раз. т.е. при
изменении частоты на одну декаду (в 10
раз),
при
изменении частоты в 10 раз. т.е. при
изменении частоты на одну декаду (в 10
раз),
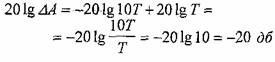 ЛАХ
уменьшается на 20 дБ, следовательно,
наклон высокочастотной составляющей
равен -20 дБ/дек.
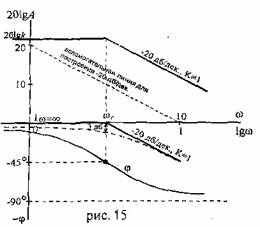
Это мы построили
приближенную характеристику. Действительная
АЧХ отличается в частоте сопряжения,
как известно из практики на 3 дБ (что
допустимо для инженерных расчетов)
(рис.15).
ЛФХ (рис.15):
ЛАХ
уменьшается на 20 дБ, следовательно,
наклон высокочастотной составляющей
равен -20 дБ/дек.
Это мы построили
приближенную характеристику. Действительная
АЧХ отличается в частоте сопряжения,
как известно из практики на 3 дБ (что
допустимо для инженерных расчетов)
(рис.15).
ЛФХ (рис.15):![]() -тангенсоида,
при
-тангенсоида,
при![]()
при ![]()
при ![]()
При![]() ЛАХ
перемещается параллельно самой себе
по оси ординат на величину
ЛАХ
перемещается параллельно самой себе
по оси ординат на величину![]() ,
ЛФХ - остается той же самой (рис.15).
,
ЛФХ - остается той же самой (рис.15).
Лекция №6
Структурные преобразования
В результате разбиения САУ на типовые звенья направленного действия и получения их передаточных функций, составляется структурная схема всей системы.
Структурная схема - это диаграмма прохождения сигналов управления и их преобразования в САУ.
Структурная схема - это математическая модель системы.
Структурные схемы для реальных САУ имеют сложный и запутанный вид. С целью упрощения структурной схемы или приведения ее к более удобному виду, можно производить структурные преобразования по определенным правилам:

|
(1) |
Правила
преобрзвания структурных схем
Преобразование последовательного
соединенных звеньев.
Решая(1)
совместно, получим ![]() или
передаточная функция двух последовательно
соединенных звеньев
или
передаточная функция двух последовательно
соединенных звеньев
|
(2) |
Итак,
при n последовательно соединённых
звеньев с передаточными
функциями![]() результирующая
передаточная функция равна произведению
передаточных функций отдельных
звеньев:
результирующая
передаточная функция равна произведению
передаточных функций отдельных
звеньев:
![]() 2.
Прсобрачованне параллельного соединенных
звеньев.
-
2.
Прсобрачованне параллельного соединенных
звеньев.
-  Решая
(1) совместно, получим
Решая
(1) совместно, получим ![]() или
или
![]() Таким
образом, перздаточная функция n параллельно
соединенных звеньев равна сумме
передаточных функций отдельных
звеньев:
Таким
образом, перздаточная функция n параллельно
соединенных звеньев равна сумме
передаточных функций отдельных
звеньев:
![]() 3.
Звено, охваченное обратной связью:
3.1.
ООС.
3.
Звено, охваченное обратной связью:
3.1.
ООС.
 Решая
(1) относительно
Решая
(1) относительно![]() и
и ![]() ,
получим:
,
получим:
![]() 3.2.
ПОС. Проводя аналогичные рассуждения,
получим:
3.2.
ПОС. Проводя аналогичные рассуждения,
получим:
![]() 3.3.
Частный случай: при единичной ОС.
Причём
знак "+" соответствует
ООС.
3.3.
Частный случай: при единичной ОС.
Причём
знак "+" соответствует
ООС.
 Знак
Знак  "-"
соответствует
ПОС.
Пример:
"-"
соответствует
ПОС.
Пример:
 обозначив
обозначив![]() и
и![]() ,получим
,получим![]() ;
Таким
образом, интегрирующее звено, охваченное
безынерционной обратной связью,
эквивалента типовому апериодическому
звену, т.е. уже не является интегрирующим.
;
Таким
образом, интегрирующее звено, охваченное
безынерционной обратной связью,
эквивалента типовому апериодическому
звену, т.е. уже не является интегрирующим.
Правила переноса сигнала
В
общем случае структурные схемы могут
иметь различного рода перекрещивающиеся
связи поэтому для приведения структуры
к одноконтурной - удобной для исследования,
разработаны правил; переноса сигналов
из одной точки структуры в другую:
1.
При прямом переносе сигнала через
ПФW1:
 2.
При обратном переносе сигнала через
ПФW1:
2.
При обратном переносе сигнала через
ПФW1:
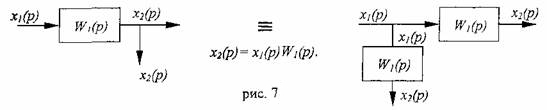 3.
При прямом переносе суммирующего
звена:
3.
При прямом переносе суммирующего
звена:
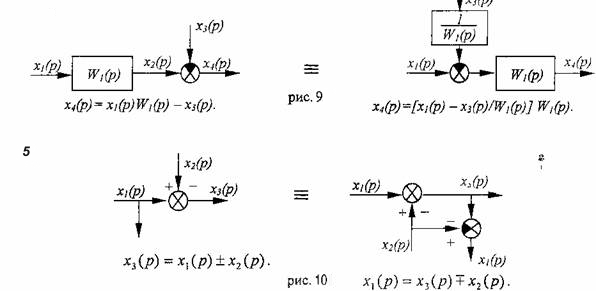
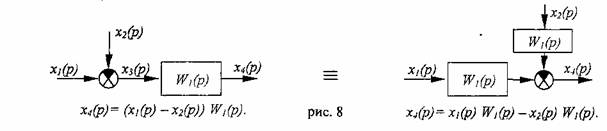 4.
При обратном переносе суммирующего
звена:
4.
При обратном переносе суммирующего
звена:
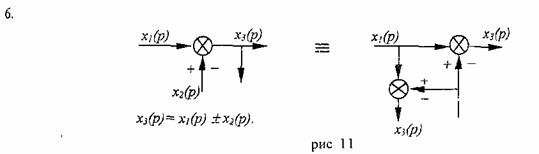
Замечание:
Структурные преобразования можно производить только в том случае, если анализ динамической системы производится при нулевых начальных условиях. В противном случае структурные преобразования приводят к потере начальных условий и погрешностям при дальнейшем анализе.
Структурные преобразования лишены физического смысла.
Лекция №7
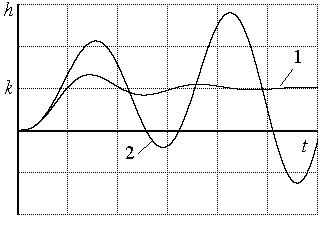
Устойчивость - это основное качественное свойство системы автоматического управления, без которого она неработоспособна. Физически устойчивость означает, что процессы в системе стремятся к определенной величине при любых начальных условиях. На рис. 1. приведены переходные характеристики неустойчивой и устойчивой системы. Для последней справедливо условие
|
Рис. 1. Переходные характеристики системы |
![]()
1 - сходящийся процесс, система устойчива. 2 - расходящийся процесс, система неустойчива.
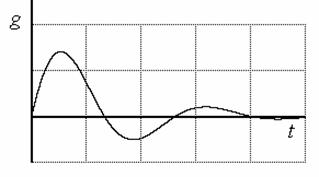
Об устойчивости можно судить также по импульсным переходным функциям (рис. 2), которые для устойчивой системы удовлетворяют условию
![]() В
случае линейных САУ устойчивость
определяется только ее структурой и
параметрами и не зависит от внешних
воздействий. Рассмотрим, как оценить
это свойство для систем типа:
В
случае линейных САУ устойчивость
определяется только ее структурой и
параметрами и не зависит от внешних
воздействий. Рассмотрим, как оценить
это свойство для систем типа:
|
Рис. 2. Импульсная переходная функция |
|
(1) |
Переходные процессы в ней определяются как решение матричного уравнения состояния следующим образом:
|
(2) |
Здесь первое слагаемое соответствует свободной составляющей движения, второе - вынужденной.
Основным режимом работы системы является равновесный (статический) режим, при котором переменные состояния с течением времени не меняются, а все производные координат состояния равны нулю.
Покажем,
что процgесс движения к равновесию можно
считать свободным. Предварительно
запишем уравнение равновесия, полагая
в (1) ![]()
|
(3) |
откуда
при det![]() A определим
равновесное значение переменных
состояния
A определим
равновесное значение переменных
состояния
|
(4) |
Введем новые координаты, равные отклонениям от точки равновесия,
|
(5) |
и запишем уравнение в отклонениях:
|
(6) |
После
подстановки в (6) вместо ![]() его
значения из (1) с учетом (5) получим
его
значения из (1) с учетом (5) получим
![]()
Окончательно уравнение в отклонениях имеет вид:
|
(7) |
Определение. Линейная система называется устойчивой, если для ее процессов выполняется свойство:
|
(8) |
Вид процессов системы (7) определяется ее решением, которое находится через матричную экспоненту в виде
|
(9) |
Поскольку выражение (9) соответствует первой составляющей решения (2), то устойчивость линейной системы (1) определяется только свойствами автономной системы и не зависит от внешних воздействий. Это означает, что можно не переходить к уравнениям в отклонениях от состояния равновесия, а для анализа устойчивости исследовать свойства матрицы A.
Лекция №8
Устойчивость (продолжение). (Алгебраические критерии устойчивости.)
![]() W
= ∑ простые звенья.
W
= ∑ простые звенья.
![]() ,
где
,
где![]() ,
,![]() -
корень полинома знаменателя передаточной
функции W.
-
корень полинома знаменателя передаточной
функции W.
Пример:
![]() ,
, ![]() .
При
.
При ![]() ,
устойчивая система.
,
устойчивая система.
 .
Если
.
Если ![]() -
положительные числа, то система
устойчивая.
-
положительные числа, то система
устойчивая.
Пример:
![]() система
неустойчивая. Т.к.
система
неустойчивая. Т.к. ![]() -
положительное числа, а
-
положительное числа, а ![]() -
отрицательное.
-
отрицательное. ![]()
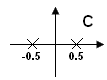 Т.к.
не все корни знаменателя находятся в
левой полуплоскости плоскости С, то
система неустойчивая (есть одна растущая
экспонента).
Т.к.
не все корни знаменателя находятся в
левой полуплоскости плоскости С, то
система неустойчивая (есть одна растущая
экспонента).
Определение: Корни знаменателя W называются полюсами. Корни числителя W называются нулями. Комментарий:
![]() ноль:
ноль: ![]() ,
полюса:
,
полюса: ![]() .
.
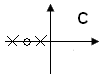 x
– полюс.
x
– полюс.
о – ноль.
Система устойчивая.
Правило: Для того, чтобы система была устойчивой необходимо и достаточно, чтобы все полюса системы находились в открытой левой полуплоскости С.
Для анализа, синтеза необходимо уметь отвечать на вопрос: “ Лежат ли все корни в левой полуплоскости плоскости С ?” по коэффициентам полинома, не вычисляя корни:
![]() .
.
Определение: Правила, позволяющее получить ответ на вопрос об устойчивости системы без вычисления корней называются критериями устойчивости.
Имеются 2 группы критериев: алгебраические и частотные. Алгебраические: критерии Роуса и Гурвица.
Критерий устойчивости Гурвица.
Формулировка: По характеристическому полиному замкнутой системы (знаменатель передаточной функции замкнутой – всей системы) составляется определитель вида:
По диагонали выписываем коэффициенты ХПЗС
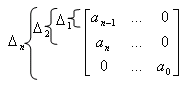 Столбцы
дополняем снизу вверх до последовательности
Столбцы
дополняем снизу вверх до последовательности ![]() .
Оставшиеся свободные места заполняем
нулями. Выделяем миноры (диагональные)
размера 1, 2,…
.
Оставшиеся свободные места заполняем
нулями. Выделяем миноры (диагональные)
размера 1, 2,…
Для
того, чтобы все корни полинома a(s)
находились в левой открытой полуплоскости
плоскости С, достаточно (и необходимо),
чтобы все ![]() были
больше 0.
были
больше 0.
Примечание:
Считаем, что ![]() .
.
Пример
1:
Пусть ХПЗС имеет такой вид: ![]() ,
, ![]() –
требуется исследовать в замкнутой
системе на устойчивость.
Составим
матрицу:
–
требуется исследовать в замкнутой
системе на устойчивость.
Составим
матрицу:
![]() {[
{[![]() ],
выделим миноры,
],
выделим миноры, ![]()
![]() Т.к.
Т.к. ![]() система
устойчива.
система
устойчива.
Пример
2:
Пусть ХПЗС имеет такой вид: ![]() ,
, ![]() .
Составим
матрицу:
.
Составим
матрицу:
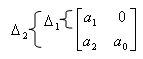 ,
,
,
, ![]()
![]() система
устойчивая
система
устойчивая
Пример
3:
Пусть ХПЗС имеет такой вид: ![]() ,
, ![]() .
Составим
матрицу:
.
Составим
матрицу:
,
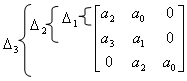
![]()
![]()
![]() система
устойчивая
система
устойчивая
Следствие:
Необходимое условие устойчивости –
положительность всех коэффициентов
ХПЗС.
Примечание:
Для Примера 3 достаточное условие
устойчивости: ![]() +
+ ![]() .
.
Лекция №9
Принцип аргумента
ХПЗС
: ![]()
Раскладывается
как: ![]()
Если р1,р2 > 0, то система устойчивая.
Возьмем ХПЗС степени n. аi – вещественные числа.
![]()
т.к. у рассмотренного полинома коэффициенты вещественные числа, то все корни : вещественные + комплексно сопряженные.
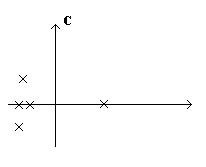 Следовательно
Следовательно ![]() (*)
(*)
![]() -
корни ХПЗС (полюса)
-
корни ХПЗС (полюса)
![]()
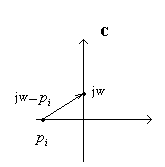
Меняя w :
(![]() )
получим, что вектор повернется на +П.
)
получим, что вектор повернется на +П.
(![]() )
повернется на +П/2.
)
повернется на +П/2.
Если
полюс слева,
то при изменении ![]() вектор
вектор ![]() повернется
против часовой стрелки(в положительном
направлении) на угол +П/2.
повернется
против часовой стрелки(в положительном
направлении) на угол +П/2.
Если справа, то угол поворота – П/2( либо -П).

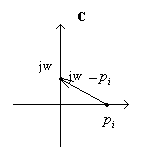
(*) s=jw
![]()
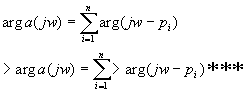
Где ∆arg изменение arg(jw) при изменении ( ) ***принцип аргумента
Критерий устойчивости Михайлова.
a(s)
– ХПЗС (знаменатель), имеет n корней и
все они лежат слева по принципу
аргумента.
Arg a(jw) = +nП/2
w:(
)

все корни слева.

Лекция №10
Устойчивость (продолжение). Критерий устойчивости Nyquista.
Требуется
по годографу ![]() (
(![]() ,
в MatLabe:
,
в MatLabe: ![]() )
сделать заключение об устойчивости
замкнутой системы.
)
сделать заключение об устойчивости
замкнутой системы.
Решение:
Рассмотрим
выражение ![]() .
.
Пусть ![]() -
отношение полиномов от s.
-
отношение полиномов от s.
![]() ,
,
deg N(s) = m – степень полинома N(s).
deg D(s) = n – степень полинома D(s).
D(s) – характеристический полином разомкнутой системы (ХПРС).
“Физически
реализуемая система” ![]() - правильная
система.
- правильная
система.
Комментарий:
u y
![]() ,
n = 1, m = 0.
,
n = 1, m = 0.
Правильная
система: ![]() ,
, ![]()
Неправильная
система: ![]() ,
, ![]()
![]() где:
где: ![]() -
ХПЗС.
-
ХПЗС.
Подставим ![]() ,
тогда:
,
тогда: ![]() .
.
Меняем
.
Тогда векторы ![]() ,
, ![]() ,
, ![]() поворачиваются
(на плоскости С), но поворот – это
изменение аргумента вектора.
поворачиваются
(на плоскости С), но поворот – это
изменение аргумента вектора.
![]() -
изменение аргумента вектора
-
изменение аргумента вектора ![]() при
изменении
.
при
изменении
.
![]() -
изменение аргумента вектора
-
изменение аргумента вектора ![]() при
изменении
.
при
изменении
.
![]() -
изменение аргумента вектора
-
изменение аргумента вектора ![]() при
изменении
.
при
изменении
.
С учетом обозначений:
![]() -
ключевая формула для критерия Nyquista.
-
ключевая формула для критерия Nyquista.
Пусть:
Разомкнутая система устойчивая![]() все
корни D(s) – слева
все
корни D(s) – слева
![]() .
Допустим,
замкнутая система оказалась устойчивой
все
корни A(s) – слева
deg
A = n
.
Допустим,
замкнутая система оказалась устойчивой
все
корни A(s) – слева
deg
A = n
![]() .
.
Пример:
![]() .
.
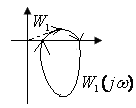
Это пример устойчивой системы замкнутой, в предположении, что разомкнутая система устойчивая.
(*)
![]()
![]()
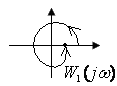
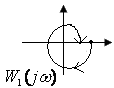
Если разомкнутая система устойчивая, а для имеем такой результат (см. *), то “что-то здесь не в порядке”.
![]() .
Для перехода к
.
Для перехода к ![]() необходимо
сдвинуть годограф
налево
на 1 (отнять 1).
необходимо
сдвинуть годограф
налево
на 1 (отнять 1).
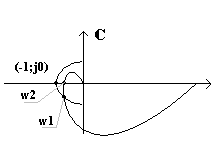
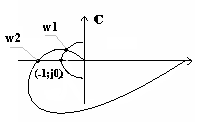
Формулировка критерия устойчивости Nyquista.
Предположение – разомкнутая система устойчивая.
Для того, чтобы замкнутая система была устойчивой, годограф разомкнутой системы не должен охватывать точку (-1, j0).
Пример 1:
Пусть ![]() ,
(k, >0)
,
(k, >0)
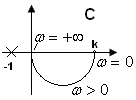
замкнутая система устойчива.
Пример 2:
k, k1, k2 >0
T > 0, 0< d < 1.
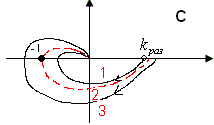 Очевидно,
что
-
устойчивая система, т.е. попали в условия
формулировки.
Очевидно,
что
-
устойчивая система, т.е. попали в условия
формулировки.
1) Устойчивая система
2) На границе устойчивости
3) Неустойчивая
При
увеличении ![]() годограф
“раздувается”.
годограф
“раздувается”.
2 вар. d – уменьшаем
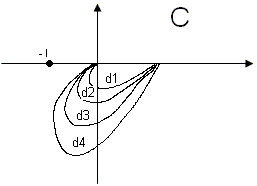 d4<d3<d2<d1
d4<d3<d2<d1
1) Замкнутая система устойчивая
2)
Если ![]() ,
то система приближается к границе
устойчивости.
,
то система приближается к границе
устойчивости.
Пусть: разомкнутая система неустойчивая, а замкнутая система – устойчивая.
Пусть у D справа r – корней и замкнутая система устойчивая.
![]()
 Если
у разомкнутой системы справа r корней,
то W повернется на
Если
у разомкнутой системы справа r корней,
то W повернется на ![]() или
или ![]() в
положительном направлении.
в
положительном направлении.
Лекция №11
Примечание:
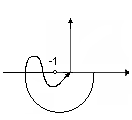
годограф не охватывает -1, значит система устойчивая.
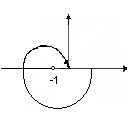
разомкнутая – устойчивая, замкнутая – неустойчивая.
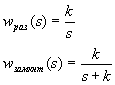
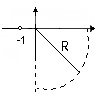
четверть окр. бесконечно
большого радиуса.
Это построение (см выше)равносильно замене интегратора апериодическим звеном, с постоянной стремящейся к 0.
Если , то нужно добавить 2 четверти окружности(пол окружности) обход по часовой стрелке.
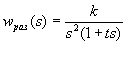 Пример:
Пример:
Дано:
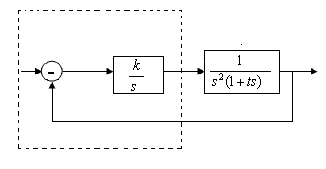
Найти: такое k чтобы система была устойчивой.
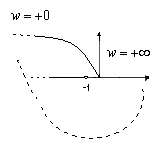
Дополненный годограф охватывает критическую точку, следовательно, система неустойчивая.
Вывод: при помощи k систему сделать устойчивой нельзя!
п.3. Устойчивость по логарифмическим характеристикам.
(Диаграммы Bode, или логарифмический аналог критерия устойчивости Nyquista)
Пусть объект имеет вид:
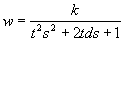 ,где
k,t,d (0,1)
,где
k,t,d (0,1)
d1>d2>d3
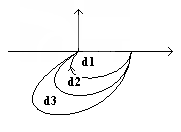
при d = 0.
Замкнутая система находится на границе устойчивости, т.е. незначительные изменения параметров объекта могут сделать систему как устойчивой так и неустойчивой.
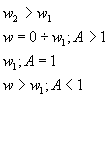
По рисунку нарисуем диаграммы bode:
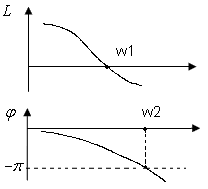
устойчивая правило: если сначала w1, а потом w2, то система устойчивая;
если наоборот, то неустойчивая.
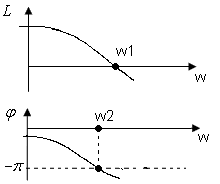
Система неустойчивая.
Лекция №12
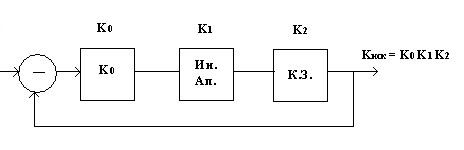
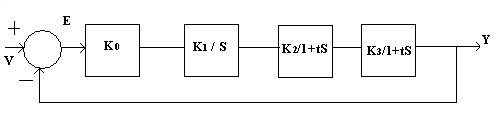
Точность в установившемся режиме. п.0. Вывод основных коэффициентов передачи.
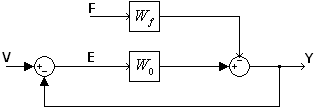
V – задание (программа),
Y – выход системы или регулируемая величина,
Е – ошибка или рассогласование,
![]() -
коэффициент передачи разомкнутой
системы,
-
коэффициент передачи разомкнутой
системы,
F – возмущение (мешает системе)
![]() -
коэффициент передачи по возмущению.
-
коэффициент передачи по возмущению.
Задача: Проанализировать точность системы установившемся режиме.
Внимание в данной лекции K - ...
Найдем изображение выходного сигнала, как функцию двух входов V,F.
Пусть: F ≡ 0.
![]() .
.
Другая ситуация: V ≡ 0.
Тогда, преобразуем к виду типовых соединений:
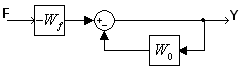
![]() .
.
Итоговая
формула: ![]()
В
идеале: ![]() ,
, ![]() .
.
Выразим формулу ошибки:
Пусть: F ≡ 0.
![]()
Другая ситуация: V ≡ 0
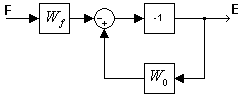
![]() .
.
Итоговая
формула ошибки: ![]()
Желательно: ![]() .
.
п.1. Входной сигнал – константа.
![]()
Найдем соотношения, связывающие параметры W со значениями задающих воздействий.
![]()
![]() .
.
?Можно
ли найти ![]()
![]()
![]()
![]()
![]() .
.
= ![]() .
.
Случай 1: не содержит интегратора.
![]()
где: K - полином от s без свободного члена.
Тогда: ![]() .
.
Полином + полином без свободных = полином без свободных.
![]()
![]() .
.
![]() .
.
Найдем
формулу ошибки в установившемся
режиме:
![]()
где ![]() -
коэффициент усиления разомкнутой
системы,
-
коэффициент усиления разомкнутой
системы,
![]() -
коэффициент передачи(усиления) по
возмущению.
-
коэффициент передачи(усиления) по
возмущению.
Пример: ![]() .
Разомкнутая система не содержит
интегратора.
.
Разомкнутая система не содержит
интегратора.
Требуется
найти ![]() .
.
Остается: ![]() .
.
Коэффициент усиления разомкнутой системы должен быть ≥ 19 (для уменьшения ошибки в установившемся режиме необходимо увеличивать коэффициент усиления разомкнутой системы).
Случай 2: содержит интегратор.
![]()
![]() .
.
Для того, чтобы ошибка была равна 0 в установившемся режиме при const на входе, в УУ необходимо ввести интегратор.
Лекция №13
Точность в установившемся режиме п.2.Линейно нарастающие сигналы.
Рассмотрим систему:
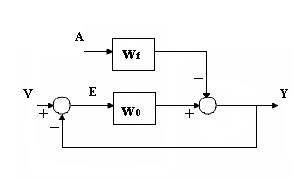
Выражение ошибки системы :
E(S)
= 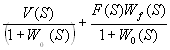
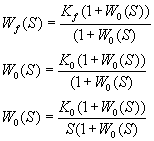
- без интегратора.
- содержит интегратор.
P>Случай 1:
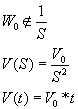 W0 объекта
не содержит интегратора.
W0 объекта
не содержит интегратора.
Линейнонарастающая функция.
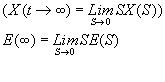
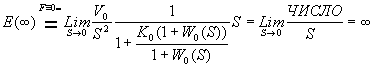
С течением времени ошибка растет неограниченно, т.е. такая система с течением времени работает все хуже и хуже.
Случай 2:
W0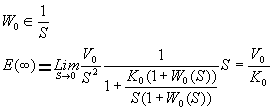 содержит
интегратор.
содержит
интегратор.
Если W0 содержит интегратор, то для линейно возрастающего сигнала, ошибка пропорциональна V0 и обратно пропорциональна K0, т.е. чтобы уменьшить ошибку необходимо увеличить K0.
п.3.Синусоидальный сигнал на входе.
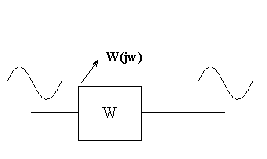
A=1
φ=0
w – задана.
На выходе будет синусоида, амплитуда и фаза которой определяется комплексным числом W(jw) для заданного w.
Например для апериодического звена
![]()
K,t – заданные числа.
Подставим w и для него получилось такое число:
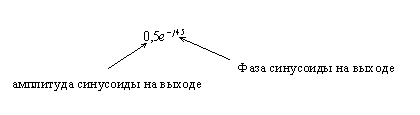
![]() Для
случая F = 0
Для
случая F = 0
![]()
Тема. 5 Синтез УУ по логарифмическим характеристикам.
Пример: (см. лекцию №11)
Используем:
критерий Nyqista:
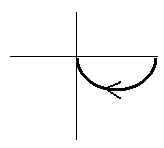
Дополненный годограф охватывает (-1;jw), следовательно система неустойчивая.
Критерий Михайлова:
![]() ХПЗС:
ХПЗС:
Годографы Михалова, случай устойчивой системы.
n- степень ХПЗС.
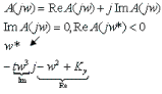
Отсюда находим w* и подставляем.
Гурвиц: система неустойчивая т.к. среди коэффициентов ХПЗС есть 0.
Лекция №14 п.0. Вводные замечания.
В начале: УУ – нет.
Для
системы у которое нет УУ, есть О построим
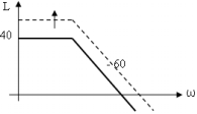
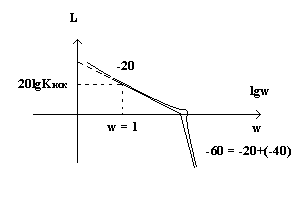
диаграмму Bode ( L , ? ).
Если диаграмма Bode выглядит следующим образом, то система устойчивая. В некоторых случаях О → Б → не устойчивая => необходимо ввести УУ. Видимо УУ должна скорректировать “----” до непрерывной линии.
Пример: Выразить по графику W.
Пример:
Взяли Система может быть устойчивой не удовлетворяющая по качеству переходного процесса – или длинный переходный процесс, или большие колебания, тогда нужно ввести УУ. 20 lg k = 20 lg 100 = 40.
Если k ↑, то диаграмма поднимается вверх => неустойчивое состояние. Изменением k можно добиться не только устойчивости, но видимо, заданного качества системы.
Можно
“доказать”, что
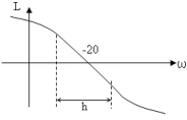
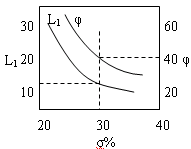
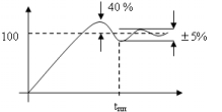
Перерегулирование σ тем больше, чем меньше участок h.. Коррекция системы – это “насилие” над системой. Поэтому нужно корректировать систему, как можно меньшей полосе частот. п.1.Диаграммы зависимости (запас устойчивости по амплитуде и фазе)
Чем L1 больше, тем перерегулирование σ меньше. Чем больше , тем время переходных процессов меньше.
Допустим необходимо, чтобы σ ? 30%. Тогда то L1 ≥ 10, φ≈400.
ωп - полоса положительности. ωср 0,8 ωп.
На частоте среза: |W(jω)| = 1 (на меньших частотах |W(jω)| > 1). На частотах больше частоты среза идет ослабление сигнала.
Допустим
нам нужно
Пример:
Пусть нам дано РГЗ, обрезанное с 2-х
концов:
Найти
УУ такое, чтобы:
См.
выше: L1 10,
lg 30 1.7. |
Лекция №15
( синтез по логарифмическим характеристикам )
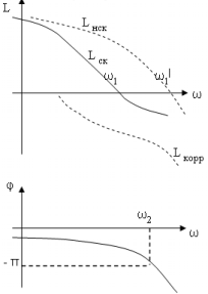
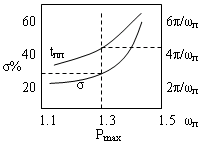
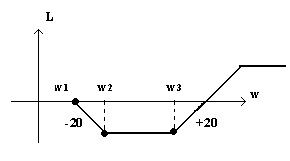
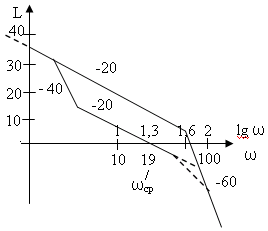
п.2. Сопряжение L желаемой с L нескорректированной.
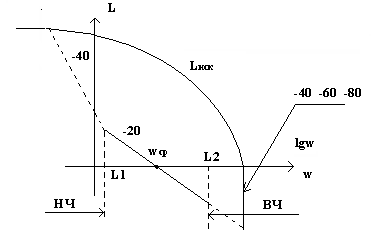
Рис.1.
L нск (см. формальное правило построения L)
Найти: w
ср -
? Если
дано: t
пп =
0,7; ![]() =
30%.
=
30%.
t пп =4.7П / w п
w ср = 08w п
Получена среднечастотная часть L ск . Нужно достроить L ск в области низких и высоких частот.
Руководствуемся принципом минимального вмешательства в частотные характеристики объекта. На НЧ и ВЧ совпадает L ск с L нск.
Примечание :
штриховые участки можно менять на 20% – 30% с целью упрощения алгебраического регулятора.(корректора).
возможны принципиально отличные варианты:
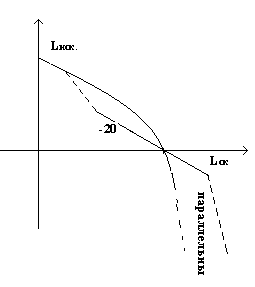

Рис.2. Рис.3.
На средних и высоких частотах мы увеличиваем коэффициент передачи нашей системы, т.е. на средних и высоких частотах мы форсируем систему.
правее от w ср – форсируем , левее – давим.
п.3. Построение L корректора (регулятора).
L нск. на графиках представляется в 2-х вариантах:
L – точная,
L – аппроксимирующая.
По рис.1:
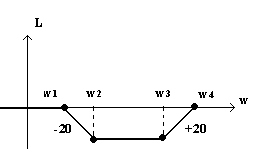
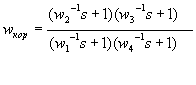
По рис.2:
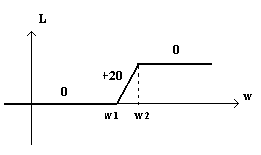
По рис.3:
Примечание : (область применения)
Wраз.нск не должна содержать нулей и плюсов.
Тема. 6 Пространство состояний (ABCD )
п.0. Введение
Здесь есть 3 дифференциальных уравнения 1-го порядка.
(A,B,C,D) – четверка матриц.
Лекция №16
Пример: Синтез по логарифмическим характеристикам.
Известно: ![]()
![]()
Требуется сделать систему устойчивой и чтобы выполнялись требования к качеству переходного процесса.
1)
Строим ЛАЧХ исходной (Lнск)
системы. Для этого необходимо убрать
обратную связь и посмотреть
![]() По
формальному правилу построения L.
Найдем
По
формальному правилу построения L.
Найдем![]() .
Необходимо отметить точку 20lg k = 20lg 50 =
34. В данной системе 2 звена: интегратор
и колебательное звено.
.
Необходимо отметить точку 20lg k = 20lg 50 =
34. В данной системе 2 звена: интегратор
и колебательное звено. ![]() ,
lg 40 = 1,6.
,
lg 40 = 1,6.
![]()
![]()
Возможные варианты решения:
 1
вариант
1
вариант
 2
вариант
2
вариант
Для
1 варианта:
![]()
Для 2 варианта:
![]()
Продолжение примера прошлой лекции:
x1, x2, x3 – выходы динамических звеньев.
Опишем данную структуру системой уравнений:
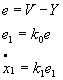
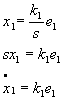
![]()
![]() ,
, ![]() .
.
![]() ,
,
![]() .
.
Желательно
алгебраические уравнения исключить.
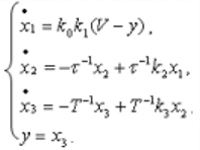
Эти 3 дифференциальных уравнения можно записать в виде:
(1)![]()
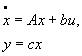 x,
y, u(t) – функции от времени t
x,
y, u(t) – функции от времени t
 ,
, 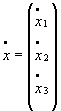 ,
где A = ,
,
где A = , 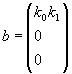 ,
, ![]() .
.
Описание системы в виде (1) называется описанием системы в пространстве состояний.
Дифференциальное уравнение (1):
Описание системы в виде (1) может быть кратко задано так:
nхn nх1 1хn
( A, b, c )
А в более общем виде:
nхn nхm mхn
(A, B, C)
n – размерность матрицы А, размерность вектора x.
m – число входов и число выходов в системе.
По (1) легко найти передаточную функцию. Для этого переходим к изображениям (при нулевых начальных условиях):
x, y, u (s) – функции от s.
![]()
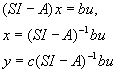
![]() .
.
Лекция №17
(пространство состояний) п.1. Понятие пространства состояний
![]()
, где Х – вектор состояний.
С = 1x2 строка.
b = 2x1 столбец.
число входов
A nxn
b nx1
C1xn
число выходов
n - размерность вектора состояний Х.
![]()
п.2. Управляемость, наблюдаемость
Пример 1:
не управляемый блок схемы.
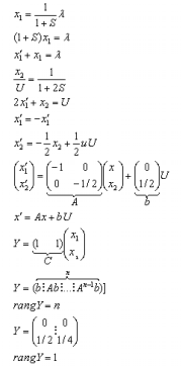
,
где ![]() какое-то
число.
какое-то
число.
Система не управляемая(см. пример) т.е. нет возможности сочинить алгоритм управления такой, что вектор состояний будет управляемый.
Примечание:
Если система не управляемая, то можно выделить управляемую и не управляемую часть.
Если не управляемая часть неустойчивая, то система неработоспособна при любом алгоритме управления.
Пример 2:
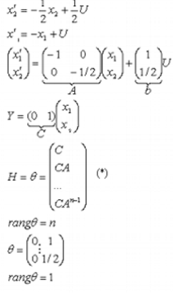
(*)- матрица наблюдаемости.
rangθ=n- наблюдаемая система, иначе нет.
rangθ=1- система ненаблюдаемая.
Примечание:
Если система ненаблюдаемая, то можно выделить ненаблюдаемую и наблюдаемую части.
Если ненаблюдаемая часть неустойчивая, то не существует алгоритма управления обеспечивающего устойчивость системы.
Утверждение:
Возможны любые сочетания свойств управляемости и наблюдаемости (лучше всего управляемая и наблюдаемая; неплохо если неуправляемые и ненаблюдаемые части устойчивые)
Пример 3:
![]()
Система управляемая, но ненаблюдаемая.
Лекция №18
п.3. Синтез.
Пусть дано описание объекта в пространстве состояний.
 ,
где b –
вектор-столбец, с –
вектор-строка
,
где b –
вектор-столбец, с –
вектор-строка
Пусть доступен для управления вектор состояния x. Требуется найти алгоритм управления такой, чтобы система имела заданный желаемый ХП (характеристический полином).
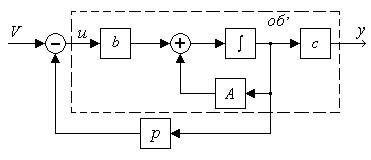
Вне штриховой лини – устройство управления.
Передаточная функция объекта:
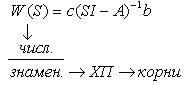
Корни (полюса), полюса характеризуют устойчивость (неустойчивость), качество переходных процессов.
Пример: Пусть первое уравнение имеет вид:
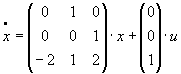 Как
найти ХП?
Как
найти ХП?
Необходимо
взять ![]() .
Если матрица А размером 3 х 3, тогда det
(определитель) матрицы
.
Если матрица А размером 3 х 3, тогда det
(определитель) матрицы ![]() будет
полином 3-ей степени.
будет
полином 3-ей степени.
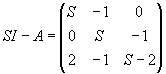 ,
,
![]() -
ХП объекта (т.е. полином знаменателя
передаточной функции). Исследуем объект
на устойчивость по Гурвицу, объект
неустойчивый (т.к. в ХП есть отрицательные
коэффициенты при S).
-
ХП объекта (т.е. полином знаменателя
передаточной функции). Исследуем объект
на устойчивость по Гурвицу, объект
неустойчивый (т.к. в ХП есть отрицательные
коэффициенты при S).
#
Система: ![]()
![]()
 Найдем
описание с учетом УУ, а именно подставим
u в
Найдем
описание с учетом УУ, а именно подставим
u в![]() :
:
![]() ,
где:
,
где:
bp – матрица размером n x n, rang (bp) = 1 (потому что она является произведением 2-х матриц, каждая из которых имеет ранг 1).
С
учетом УУ система преобразовалась к
виду: ![]()
ХПЗС
= ![]() ,
т.е. система:
,
т.е. система: ![]() +
регулятор + обратная связь. A, b – известно,
при помощи p добьемся
чего-нибудь.
+
регулятор + обратная связь. A, b – известно,
при помощи p добьемся
чего-нибудь.
Задача:
Необходимо сделать УУ такое, чтобы
имел
полюса равные -3, -3, -3. Т.е. ХПЗС ![]() .
.
![]()
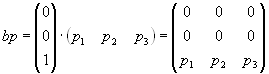 ,
rang (bp) = 1.
,
rang (bp) = 1.
Выписываем А:
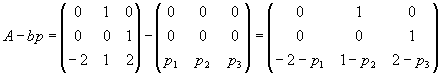
Блочная матрица:
В
примере матрица А задана в каноническом
виде, последняя строка - это коэффициенты
ХМ матрицы с “перевернутым” знаком: ![]() .
.
Подставляем: ![]() ,
отсюда мы можем легко найти
,
отсюда мы можем легко найти ![]() .
. ![]() .
#
.
#
Примечание
1:
(размышление
об РГЗ)
Пружина с гирькой без
демпфирования описывается таким
уравнением: ![]() .
Описание
в пространстве состояний:
.
Описание
в пространстве состояний: ![]() .
.
![]() ,
,  .
Ab
.
Ab
Для
реализации выше изложенного алгоритма
нам необходим вектор X, т.е. компонента ![]() -
это y, т.е. координата грузика. И
компонента
-
это y, т.е. координата грузика. И
компонента ![]() -
скорость. Нужен
-
скорость. Нужен ![]() ,
т.е. нам нужны 2 датчика: положения и
скорости.
,
т.е. нам нужны 2 датчика: положения и
скорости.
Примечание 2: Алгоритм решения простой, из-за специального вида матриц A и b. В общем случае матрица A не канонического вида.
Примечание
3: Если
матрица А задана в произвольном виде,
то переходим к другому базису ![]() ,
где Т – преобразование подобия.
,
где Т – преобразование подобия.
х
– вектор в старом базисе, ![]() -
вектор в новом базисе.
Тогда берем
1-ое уравнение:
-
вектор в новом базисе.
Тогда берем
1-ое уравнение: ![]() ,
получим
,
получим![]() .
От матрицы А перешли к матрице
.
От матрицы А перешли к матрице ![]() -
это подобное преобразование матриц,
свойства не меняются, так получают
каноническую форму.
-
это подобное преобразование матриц,
свойства не меняются, так получают
каноническую форму.
Лекция №19
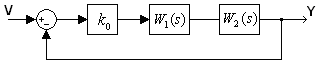
Алгебраические методы синтеза.

WR- Регулятор или УУ Wo- Объект V- Задание или программа. E- Ошибка Y- Выход - - - часть которую надо реализовать. U- Вход объекта и выход регулятора.
ример
1: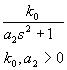
Пусть объект имеет такой вид:
Задачи:
добиться устойчивости.
выбрать такой алгоритм управления, чтобы ХП системы замкнутой соответствовал заданному.
Попытка 1:
Пусть WR пропорциональное звено. WR= Х0.
Находим ХПЗС для этого вначале находим Wраз , а затем Wзам :
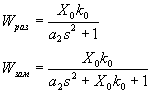
Выписываем
ХПЗС: ![]() .
Коэффициент при S в первой степени равен
0,
следовательно добиться устойчивости
нельзя.
.
Коэффициент при S в первой степени равен
0,
следовательно добиться устойчивости
нельзя.
Попытка 2:
Возьмем:
![]()
Находим Wраз:
![]()
Выписываем ХПЗС:
![]()
Выбором x,y>0 добиваемся положительных коэффициентов полинома, т.е. необходимое условие устойчивости выполнено(Гурвиц).
Произведение средних > произведения крайних
![]()
Эта задача квадратичного программирования, и здесь по- видимому решение есть.
![]()
Потребуем
чтобы ХП системы был равен заданному.
Например, ![]()
Т.е. все корни плоскости С лежат в левой полуплоскости и например равны -1.
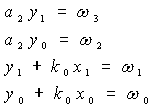
![]() получили
систему линейных уравнений.
получили
систему линейных уравнений.
Запишем в матричной форме:
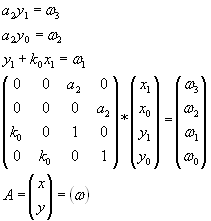
Ранг А = 4, решение есть. Примечание: точность системы в установившемся режиме определяется коэффициентом усиления разомкнутой системы и может оказаться неудовлетворительной.
Допустим требуется обеспечить астатизм(т.е. ошибка в установившемся режиме равна 0)
Астатизм обеспечивается введением интегратора в закон управления. В нашем случае нужно взять Y0.
Можно перерисовать :

Y0 известно, Y0 = 0.
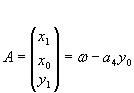
Эта система почти всегда не имеет решений.
Попытка 3:
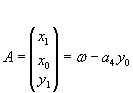
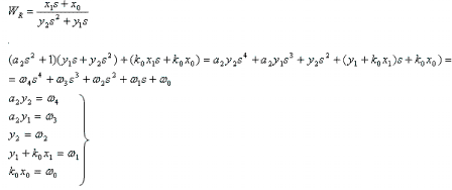
Очевидно, что эта система почти всегда не имеет решения, т.е. матрица А- вырожденная.
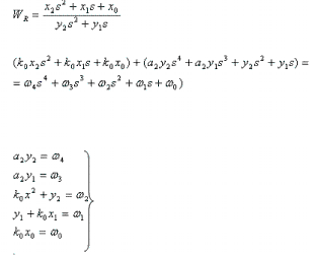
Попытка 4:
Система почти всегда имеет решения.
Задачи для экзамена
№ 1

Требуется: обеспечить устойчивость для этой системы (решать алгебраически).
№ 2
Требуется: обеспечить устойчивость. Примеч.: синтез по ЛАЧХ можно делать только для объектов у которых нули и полюса слева (а здесь полюса и слева, и справа).
№ 2*
В
задаче № 2: ![]() .
(Теперь можно по ЛАЧХ)
.
(Теперь можно по ЛАЧХ)
№ 3
Дано: ![]() ,
, ![]()
Провести синтез УУ по ЛАЧХ.
№ 3*
Дано: ![]() ,
,
Провести синтез УУ по ЛАЧХ.
№ 4
Дано: ![]() ,
, ![]()
Провести синтез УУ по ЛАЧХ.
Лекция №20
Дискретные (цифровые системы)
Тема.1 Импульсный элемент (идеальный)
п.0. Введение
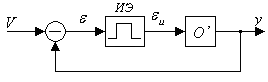
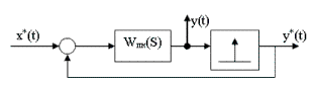
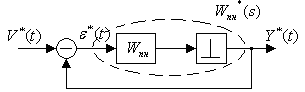
Рассмотрим систему управления в вычислительным устройством в УУ:
Ранее мы предполагали, что период квантования достаточно маленький и дискретностью по времени можно пренебречь. Например, если наименьшая постоянная (инерционность) больше периода квантования, например больше на 2 порядка, то дискретностью по времени можно пренебречь.
УУ включает в себя алгоритм вычисления и вносит дискретность по времени, т.е. УУ можно представить так:
Алгоритм “отнесем” к объекту (непрерывная часть), тогда система управления + объект может быть зарисована в виде такой системы:
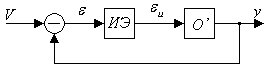
где ИЭ – импульсный элемент.
Допустим:
![]() -
период квантования, импульсы определенной
формы модулируемые сигналом.
-
период квантования, импульсы определенной
формы модулируемые сигналом.
Примечание: “Хвосты” импульсов могут накладываться:
 ---- -
---- - ![]()
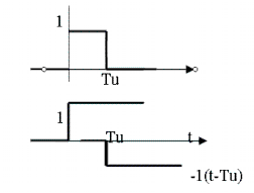
Хвосты могут тянуться долго, они меняют вид сигнала. Как правило будем считать, что импульсный элемент генерирует прямоугольные импульсы.
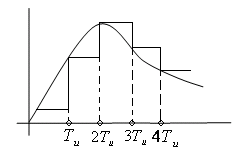
- период квантования
п.1. Эквивалентная схема импульсного элемента
Схема импульсного элемента:
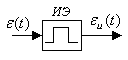
Его эквивалентная схема
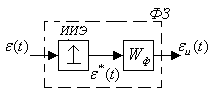
ИИЭ – идеальный импульсный элемент, ФЗ – формирующее звено. Эта схема должна функционировать эквивалентно одному квадрату.
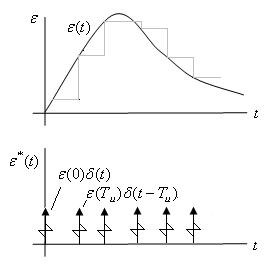
Последовательность
модулированных ![]() -
импульсов.
-
импульсов.
![]() -
формирует прямоугольные импульсы.
-
формирует прямоугольные импульсы.
![]() (изображение
по Лапласу).
Известно:
(изображение
по Лапласу).
Известно:
![]()
![]()
Итак,
получим:![]() .
.
![]()
Таким образом система с вычислителем может быть преобразована к такой структуре:
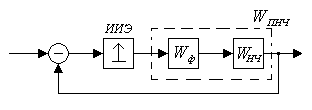
НЧ – непрерывная часть (там находятся объект и алгоритм счета),
- формирование из - импульса прямоугольный импульс,
ИИЭ – идеальный импульсный элемент (выдает последовательность - импульсов),
![]() -
приведенной непрерывной части.
-
приведенной непрерывной части.
Задачи для экзамена
№ 5
Прикладывается некоторое напряжение, необходимо найти передаточную функцию W и все ее характеристики.
№ 6
Дано: ![]() .
Синтез по L (известны σ и tпп)
.
Синтез по L (известны σ и tпп)
№ 7
Дано: ![]() .
Синтез по L (известны σ и tпп)
.
Синтез по L (известны σ и tпп)
№ 8
Дано: ![]() .
Алгебраический синтез.
.
Алгебраический синтез.
№ 9
Дано: ![]() .Требуется
нарисовать L и φ (диаграмму Bode)
.Требуется
нарисовать L и φ (диаграмму Bode)
№ 10
Необходимо написать передаточную функцию W и нарисовать L.
п.2. Изображение дискретного сигнала
Последовательность модулируемых - импульсов:
![]()
Примечание:
![]() ,
* - признак что сигнал дискретный.
,
* - признак что сигнал дискретный.
Изображение
дискретного сигнала: ![]()
![]()
![]() .
.
Иногда: ![]()
![]() (обозначают
через Z ), Z – сдвиг по времени на такт
вперед
(тоже самое, как нет оператора
дифференцирования - физически).
Т.е. правую часть можно записать так:
(обозначают
через Z ), Z – сдвиг по времени на такт
вперед
(тоже самое, как нет оператора
дифференцирования - физически).
Т.е. правую часть можно записать так:
![]() -
изображение дискретного сигнала по
переменной Z.
-
изображение дискретного сигнала по
переменной Z.
Если
Z – сдвиг по времени на такт вперед,
то ![]() -
запаздывание на такт.
-
запаздывание на такт.
Генератор импульсов:
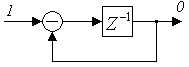
Лекция №21
(п.2. Изображение дискретных сигналов)
*- признак дискретного по времени сигнал.
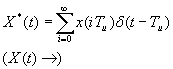
последовательность δ- импульсов сдвинутых по времени iTu и модулированных сигналом X(t) cоотв.значением Х(iTu).
п.3. Передаточная функция импульсной системы
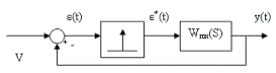 Найдем
передаточную функцию этой системы(связь
между изображением входа и выхода).
Звено ИИЭ перенесем налево:
Найдем
передаточную функцию этой системы(связь
между изображением входа и выхода).
Звено ИИЭ перенесем налево:
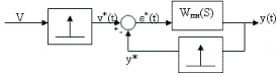
a δ(t) –b δ(t) = (a-b) δ(t)
Структурное преобразование эквивалентно:
V Y ε
a δ(t) –b δ(t) = (a-b) δ(t)
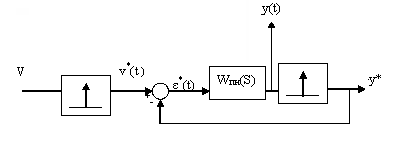
Будем искать передаточную функцию между 2-мя точками.
Зная связь между V*(t)>-->Y*(t) легко восстановить связь между V(t)-->Y(t)(но для дискретных моментов времени).
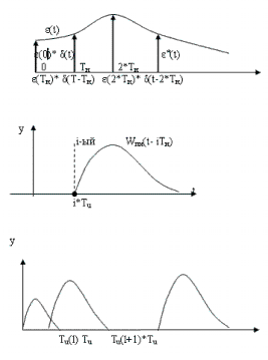

На рис.5а последовательность δ(t)- импульсов это ε*(t).
импульсная переходная ф-ия
Нас интересует реакция системы в момент времени t, который лежит в пределах l* Tu ≤ t ≤ (l + 1)* Tu . Нужно рассмотреть воздействие импульсов приложенных на тактах 0, 1, …l(будущее не влияет на настоящие).
Система линейная, справедлив принцип суперпозиции, т.е. реакция системы будет равна сумме реакций. Будем брать t в дискретные моменты Tu.
Формулы:
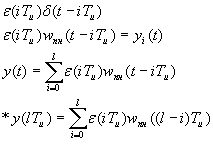
Комментарий(к *):
Предел
вверху l можно заменить на ![]() .
.
t < 0 => ωпн(t) = 0, т.к. на будущее воздействие системы не реагирует.
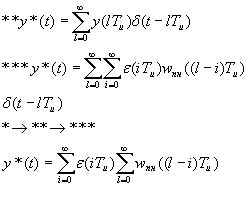
Введем ![]() :
:
![]()
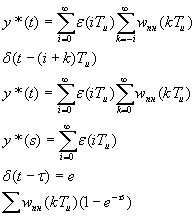
Лекция №22
(Передаточная функция импульсной системы)
![]()
![]() -
импульсная переходная функция.
-
импульсная переходная функция.
Переход к изображениям:
![]()
Известно,
что: ![]()
![]()
Сделаем преобразование:
![]()
![]()
![]()
Дискретная
передаточная функция: ![]()
![]()
![]()
![]()
Примечание: Допустим дано выражение:

![]() ,
сумели представить в виде
ряда, где
,
сумели представить в виде
ряда, где ![]() .
То тогда
.
То тогда ![]() -
дискретное значение переходной
характеристики передаточной функции.
-
дискретное значение переходной
характеристики передаточной функции.
Если дана импульсная переходная характеристика
п.4.Передаточная функция замкнутой дискретной системы
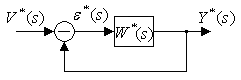
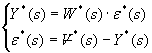
![]() .
.
Исключаем ![]() получаем
большое выражение и находим связь
между
получаем
большое выражение и находим связь
между ![]() и
и ![]() .
.
Пример
1:
Дано: ![]()
![]()
![]() =
=
Обозначим ![]() ,
то получим убывающую геометрическую
прогрессию.
,
то получим убывающую геометрическую
прогрессию.
=![]() ,
где Z
,
где Z ![]() .
.
Z – краткое обозначение оператора сдвига по времени на такт вперед.
Примечание:
![]() -
звено (оператор) запаздывания на такт.
Можно строить структуры содержащие
звено
запаздывания
.
В дискретных системах
играет
туже роль, что интегратор в непрерывных
системах.
-
звено (оператор) запаздывания на такт.
Можно строить структуры содержащие
звено
запаздывания
.
В дискретных системах
играет
туже роль, что интегратор в непрерывных
системах.
![]() .
.
Получили сопоставления изображения непрерывного и дискретного изображения.
п.5.Устойчивость дискретных систем
Пусть
дано: ![]() -
передаточная функция замкнутой дискретной
системы
-
передаточная функция замкнутой дискретной
системы
![]()
Лекция №23
![]()
![]()
k*,A* - полиномы от Z.
![]()
(*) – ХПЗС.
Для устойчивости все его корни должны лежать в левой полуплоскости плоскости С .
Но
полином функция от ![]() ,
S=j(w+wn)+α –
комплексная переменная. Можно показать,
что экспонента функция периодическая
с периодом по мнимой оси. Период
,
S=j(w+wn)+α –
комплексная переменная. Можно показать,
что экспонента функция периодическая
с периодом по мнимой оси. Период
WИ=2П/ТИ
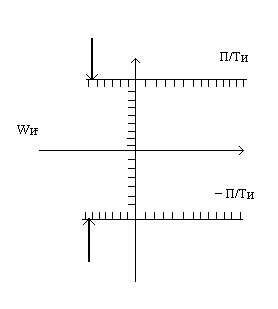
Для устойчивости необходимо и достаточно, чтобы корни ХПЗС лежали в левой половине полосы.
От S --> Z:
Легко показать, что при переходе от S к Z левая полуплоскость на плоскости Z отобразится в единичную окружность.
![]()
Для устойчивости (**) корни должны лежать в единичном круге, т.е. по модулю быть меньше 1.(если лежит на единичной окружности, то на границе устойчивости).
Введем переменную : V= z-1/z+1.
В новой переменной внутренность единичного круга отображается в левую полуплоскость плоскости V.
![]()
Вывод: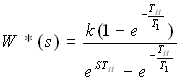 сделав
цепочку преобразований Sà Zà V
получаем ХПЗС переменной V, применяем
критерии из непрерывной теории.
сделав
цепочку преобразований Sà Zà V
получаем ХПЗС переменной V, применяем
критерии из непрерывной теории.
Дано: Требуется исследовать замкнутую систему на устойчивость
Т1 – инерционность.
ТИ – период квантования.
К – коэффициент усиления.
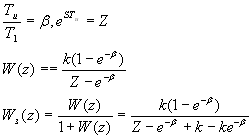
Будем исследовать систему по Гурвицу. Берем ХПЗС:
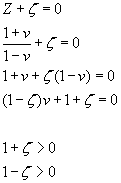
Необходимо и достаточно чтобы система была устойчивой.
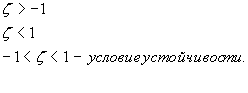
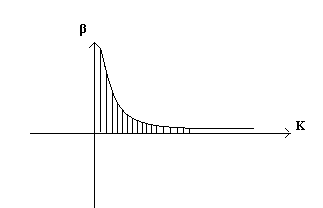
Область устойчивости.
Лекция №24
(Передаточная функция замкнутой дискретной системы)
Передаточная
функции замкнутых дискретных систем –
есть отношение полиномов от ![]() .
.
![]() ,
при
,
при ![]() .
.
Делим
левую часть (числитель и знаменатель)
на ![]() .
Тогда получим следующее выражение:
.
Тогда получим следующее выражение:
![]() .
.
Преобразуем далее:
![]() ,
,
![]()
Переходим к оригиналам:
![]() ,
, ![]()
![]()
Возьмем ![]() ,
где
,
где ![]() -
целое. Тогда:
-
целое. Тогда: ![]() ,
, ![]() .
Итак, получим:
.
Итак, получим:
![]()
Получили дискретное соотношение вх/вых, необходимо избавиться от .
Проинтегрируем
уравнение по времени ![]() .
.
![]()
Обозначим ![]()
![]() и
подставим, получим следующее выражение:
и
подставим, получим следующее выражение:
![]()
Задание к расчетно -графической работе.