22. Потужність в режимі гармонічних коливань

Розглянемо ділянку електричного кола, напруга та струм якої дорівнюють відповідно:

, тобто струм відстає від напруги (індуктивний характер кола). Миттєва потужність, яка надходить у коло:

= .

Вона має дві складові: постійну та гармонічну з подвоєною кутовою частотою відносно напруги та струму.

Активна потужність, що надходить у коло:

,

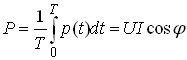так як середнє значення другого доданку за період дорівнює нулю.

Множник cos? має назву коефіцієнта потужності. Таким чином, активна потужність дорівнює додатку діючих значень напруги та струму, помноженому на коефіцієнт потужності. Чим менше ? (??0), тим ближче буде коефіцієнт потужності до 1 (cos??1) і тим більшою при заданих U та I буде активна потужність, яка передається джерелом до приймача. Підвищення коефіцієнта потужності промислових електроустановок є досить важливою техніко-економічною проблемою. Останнім часом вимоги до cos? з’явилися навіть для відносно малопотужних (десятки-сотні Вт) імпульсних джерел електроживлення (ІДЕЖ), що живлять персональні комп’ютери. Для підвищення cos? в малопотужних системах використовують спеціальні пристрої PFC (power factor control) – коректори. Активну потужність можна визначити також за такими формулами:

,

або через активні складові напруги та струму: .

Наведені вирази для миттєвої та активної потужності можуть бути застосовані і до розглянутих раніше часткових випадків коли .

Розглянемо активно-індуктивне коло (0<?<?/2; 0<cos?<1). Часові діаграми наведені на рис27. Миттєва потужність змінюється з кутовою швидкістю 2? відносно постійної складової .

У проміжки часу, коли u(t) та i(t) мають однакові знаки, миттєва потужність додатна (енергія надходить від джерела до приймача, перетворюючись у теплоту в активному опорі та накопичуючись у магнітному полі індуктивності).

У проміжки часу, коли u(t) та i(t) мають різні знаки, миттєва потужність від’ємна і енергія частково передається приймачами до джерела. Аналогічні процеси відбуваються у випадку активно-ємнісного кола (-?/2<?<0).

Величина, що дорівнює добутку діючих значень струму та напруги, називається повною потужністю:

[BA].

Очевидно, що коефіцієнт потужності можна виразити через активну та повну потужності :

.

При розрахунку електричних кіл, а також на практиці використовують поняття реактивна потужність:

[BAp].

Реактивна впотужніть є мірою споживання або генерації реактивного струму. Справедливими будуть також наступні співвідношення:

Звідси видно, що:

;

Реактивна потужність додатна при ?>0 (індуктивний характер кола) та від’ємна при ?<0 (ємнісний характер кола).

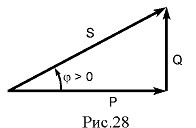
Графічно зв’язок між P, Q, S можна подати у вигляді прямокутного трикутника – трикутника потужностей (рис28). На щитку будь-якого джерела електричної енергії змінного струму вказують значення повної потужності S, що характеризує ту потужність, яку це джерело може віддати споживачу, якщо останній працює з cos?=1 (чисто активний опір).

23. Методика розрахунку rc і rl ланок.

Ця формула нагадує формулу закону Ома. Величину  називають повним опором (імпедансом) кола змінного струму, а величину  — індуктивним опором кола. За допомогою експериментальних досліджень цю формулу легко підтвердити.

У реактивних навантаженнях енергія електричного струму в певні інтервали часу переходить в енергію електричного поля конденсатора чи магнітного поля котушки, а в інші — енергія повертається в електричне коло

Реактивні навантаження бувають індуктивними і ємнісними. Опір індуктивного навантаження

, а опір ємнісного —

Рівняння можна використати для графічного   зображення   величин,   що характеризують змінний струм. Значення ImaxRsin дає коливання спаду напруги на активному опорі, а значення ImaxLcos — коливання спаду напруги на індуктивному опорі:

Отже, коливання напруги на індуктивному  опорі  випереджають   коливання   напруги на активному опорі на  і на векторній діаграмі ці напруги будуть взаємно перпендикулярні (мал. 3.10).

Вся система векторів обертається проти годинникової стрілки з кутовою швидкістю w і проекція вектора  на вісь X у будь-який момент часу дає миттєве значення електрорушійної сили , а проекції векторів  — миттєві значення спадів напруг, відповідно, на активному й індуктивному опорах.

Очевидно, що tgco не залежить від значення сили струму. Тому для знаходження повного опору можна скористатися так званим прямокутним трикутником опорів (мал. 3.11).

У колі змінного струму з ємністю сила струму випереджає напругу в ідеальному випадку (R = 0) на . Для миттєвих значень сили струму і напруги в колі з ємністю маємо:

Ємнісний опір у колі змінного струму визначається ємністю кола і частотою змінного струму. Як теоретично, так і експериментально можна легко встановити формулу для знаходження ємнісного опору:

де Rc — ємнісний опір, Oм; С — ємність кола, Ф.

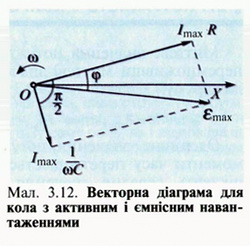
Векторна діаграма для кола з ємністю зображена на мал. 3.12.

Трикутник опорів (мал.3.13)

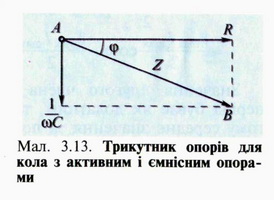
і для цього випадку дає змогу досить легко знаходити повний опір кола:

Зрозуміло, що індуктивний і ємнісний опори можна визначити не лише через колові частоти w, а й через звичайні частоти f та періоди Т змінного струму.

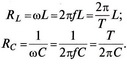
Перш ніж перейти до розгляду спільної дії індуктивності і ємності в колі змінного струму, розглянемо питання про потужність змінного струму.