Деформационные свойства бетона при кратковременном силовом воздействии

1. Центральное осевое сжатие:

∆l=∆l₁ + ∆l₂ ; E=∆l/l₀ ; ∆а=∆а₁ + ∆а₂ ; Е_п = ∆а/а ; σ = F/А ; А=а².

где: ∆l – продольная деформация

∆а – поперечная деформация

Е – относительная деформация, отнесенная к первоначальному размеру

Относительной деформации могут быть продольные и поперечные.

А- первоначальная площадь

F – действующая сила

σ – механическое напряжение

μ = Е_п / Е - коэффициент поперечных деформаций

Деформативные свойства бетона при осевом сжатии характеризуются зависимостью «напряжения- деформации», которая называется диаграммой «σ-ε», причем возможно изучение деформаций, т.е. получение диаграммы «σ-ε» как в продольном, так и в поперечном направлении. Для удобства практического применения деформации бетона представляют в относительном виде – как отношение абсолютного значения деформации к первоначальному размеру образца. Деформативные свойства бетона учитываются при расчете деформаций железобетонных конструкций ( прогибов плит и т.д.). Вследствие наличия у бетона упругопластических свойств его диаграмма «σ-ε» является нелинейной. Для характеристики деформативных свойств бетона используются такие параметры деформирования, как модуль деформаций, коэффициент упругости, коэффициент пластичности и величина деформаций, соответствующая пределу прочности бетона.

Модулем деформаций бетона называется отношение величины напряжения к соответствующей ему относительной деформации:

Е=σ/ε

Очевидно, что в силу нелинейности диаграммы «σ-ε» Е= const.

Деформативность бетона зависит от деформативных свойств его компонентов (цементного камня и заполнителей), их объемной концентрации, продолжительности и условий твердения. Модуль упругости тяжелых бетонов возрастает в диапозое от 20*10³ до 65*10³ МПа при повышении предела прочности при сжатии от 15 до 150 МПа. Модуль упругости тяжелых бетонов повышается с увеличением модуля упругости крупного заполнителя и его объемного содержания в бетоне ( определяется по формуле О.Я. Берга). Влияние времени твердения на модуль упругости тяжелого бетона менее выражено, чем на прочность.

Связь модуля упругости бетона с пределом прочности при сжатии неоднозначна и характеризуется отклонением расчетных значений от фактических до 30%.

Диаграмма напряжения деформаций

σ

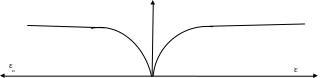
Зависимость напряжения от деформации называется «σ»-«ε» называется диаграммой или диаграммой напряжений деформации.

Параметры «σ»-«ε» диаграммы для предельных деформаций

`

1. «σ»-«ε» диаграмма бетона криволинейна, имеет восходящую и низко ходящую ветвь.

2. Модулем деформации называется t_д угла наклона секцией, проходящей через начало координат и любую точку диаграммы. С увеличением напряжения модуль деформацией уменьшается.

3. Начальным модулем упругости бетона условно называется модуль деформацией, соответствующей уровню напряжения, составляющего 30% предела кратковременной прочности: Е₀ = Е {σ = 0,3R} – начальный модуль упругости бетона; в европейских нормах ЕN модуль деформации, соответствующей уровню напряжения, составляет 40% предела кратковременной прочности.

4. Уровень нагружения 30% от максимального (40% в EN) условно упругой работы бетона. В любой точки диаграммы при напряжениях, превышающих условный предел упругости, деформация состоит из 2-х составляющих:

- упругой

- не упругой

ε = ε_еl + ε_pl; ε_el = σ / Е₀; σ >0,3*R

Коэффициентом упругости называется отношение упругой деформации к полной в любой также точке диаграммы:

λ_еl=ε_еl / ε

Коэффициенты пластичности называется отношение неупругой деформации к полной в любой точке диаграммы:

λ_pl = ε_pl / ε В сумме: λ_еl + λ_pl = 1

Динамическим модулем упругости (Ed) называется модуль деформации при напряжении, равном нулю (т.е. в начале координат):

E_d = f (ρ,μ,v)

где: μ – коэффициент Пауссона ;

v – скорость распространения продольных колебаний в материале (характеристика упругих свойств материалов) ;

ρ – плотность материала.

С увеличением уровня напряжений доля неупругих деформаций в полной деформации возрастает.

Предел кратковременной прочности R, начальный модуль упругости Е₀, коэффициент упругости, соответствующий пределу кратковременной прочности (λ_R/ε_R) называются основными константами деформирования бетона: