Алгоритм решения игрока а.
По оси абсцисс откладываем отрезок единичной длины.
По оси ординат откладываем выигрыши при стратегии (
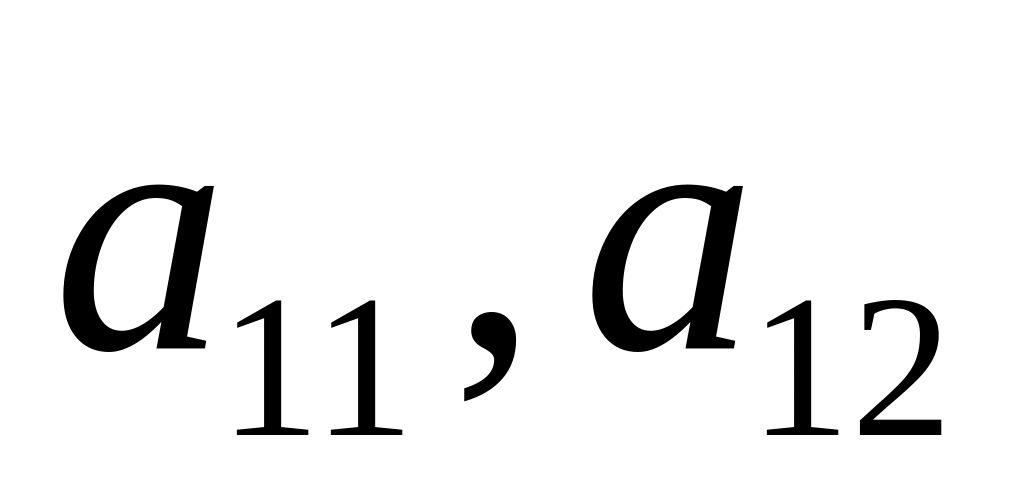).По вертикали в точке откладываем выигрыши при стратегии (
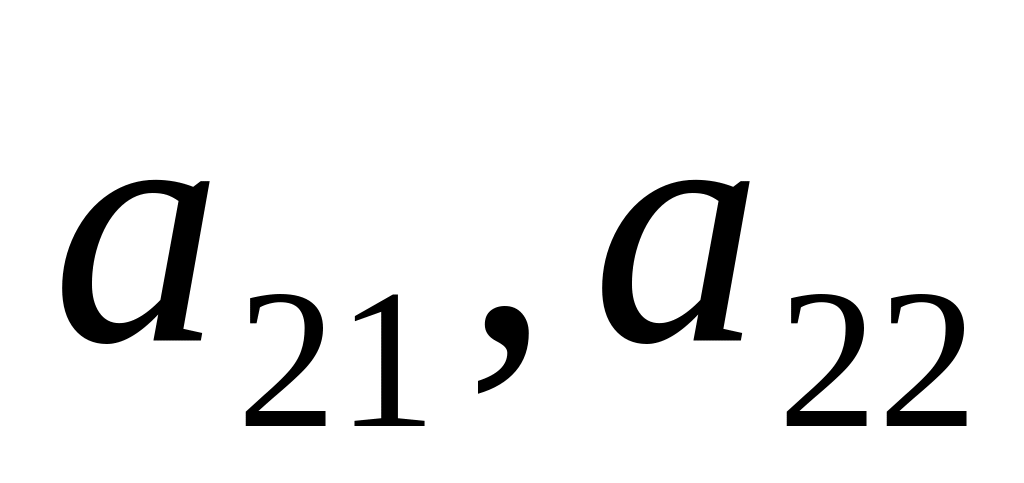).Проводим прямую через точки
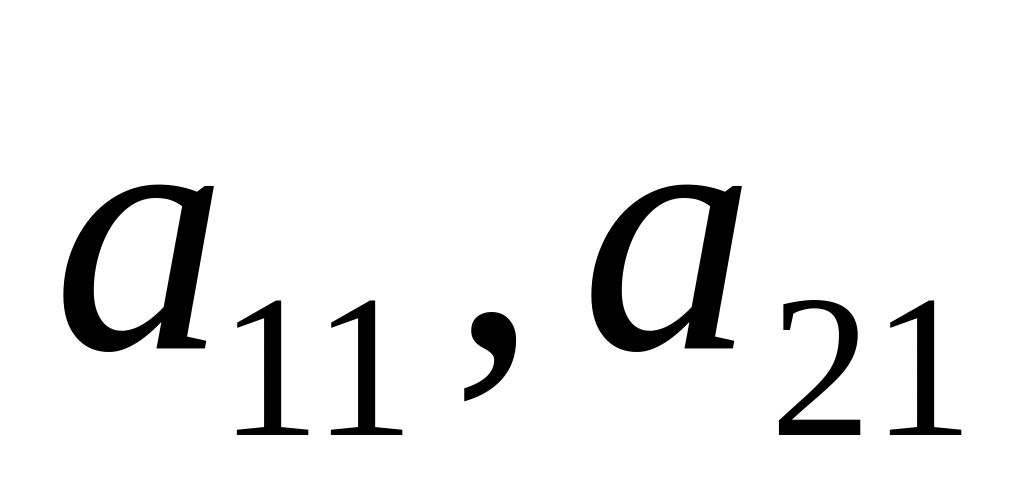.Проводим прямую через точки
.Ордината точки – точки пересечения прямых и равна цене игры .
Абсцисса точки равна
;
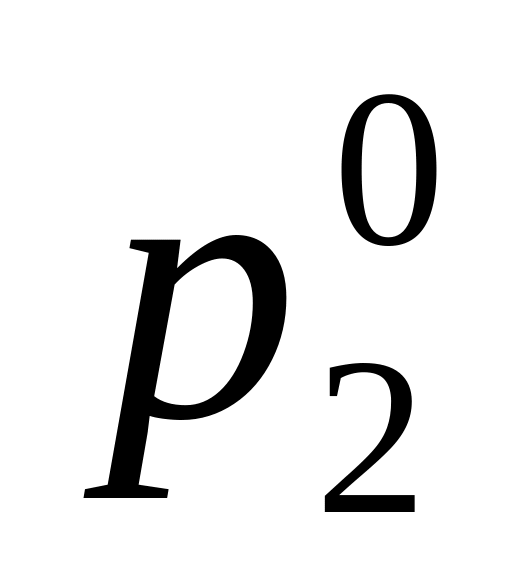.Оптимальная смешанная стратегия игрока : .
Чтобы определить координаты точки , нужно найти уравнения прямых и .
Запишем в общем виде уравнение прямой, проходящей через две данные точки:
.
Прямая
проходит через точки с координатами
и
(рис. 7). Следовательно,
,
,
,
.
Уравнение прямой
:
.
Аналогично
находим уравнение прямой
.
Прямая
проходит через точки с координатами
и
.
Следовательно,
,
,
,
.
Уравнение прямой
:
.
Точка является точкой пересечения прямых и . Чтобы найти ее координаты, нужно решить систему уравнений:
.
.
,
.
Ординату
точки
можно найти, подставив значение
в любое из уравнений системы (например,
в первое):
.
Следовательно,
цена игры
.
Оптимальная смешанная стратегия игрока :
.
Геометрически
можно также определить оптимальную
стратегию игрока
,
если поменять местами игроков
и
и вместо максимума нижней границы
в соответствии с принципом минимакса
(рис.13), рассмотреть минимум верхней
границы
.
Абсцисса
точки
определяет
в оптимальной стратегии игрока
,
ордината этой точки – цена игры.
Алгоритм решения игрока .
По оси абсцисс отложим отрезок единичной длины.
По оси ординат отложим выигрыши при стратегии ( и )
По вертикали в точке отложим выигрыши при
стратегии
(
и
).
Проводим прямую
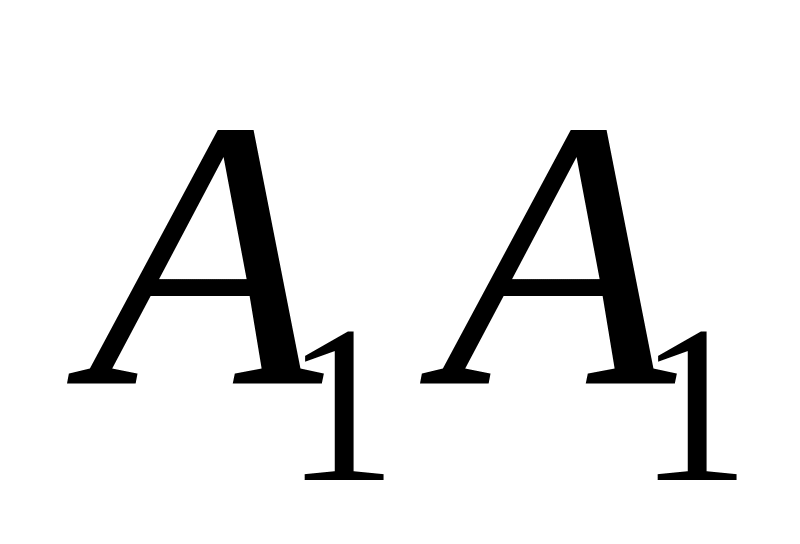через точки
и
.Проводим прямую
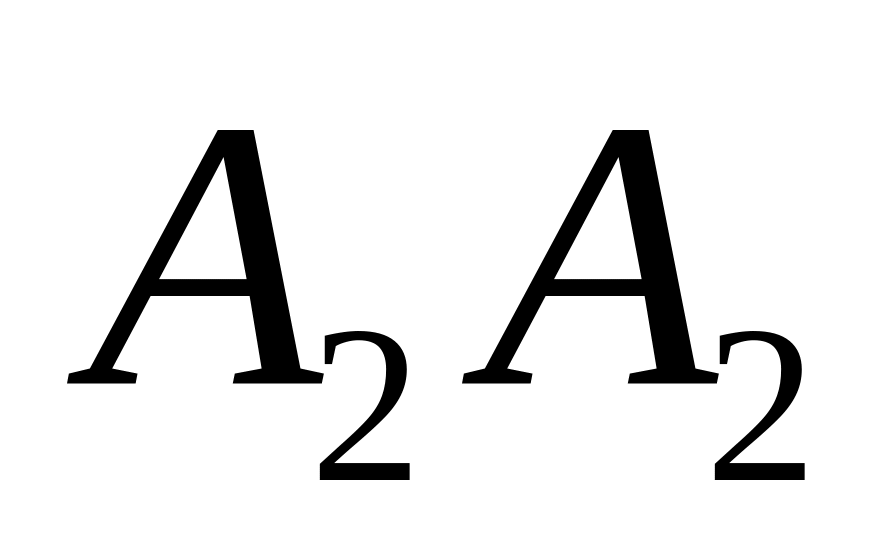через точки
и
.Ордината точки – точки пересечения прямых и равна цене игры .
Абсцисса точки равна ;
.
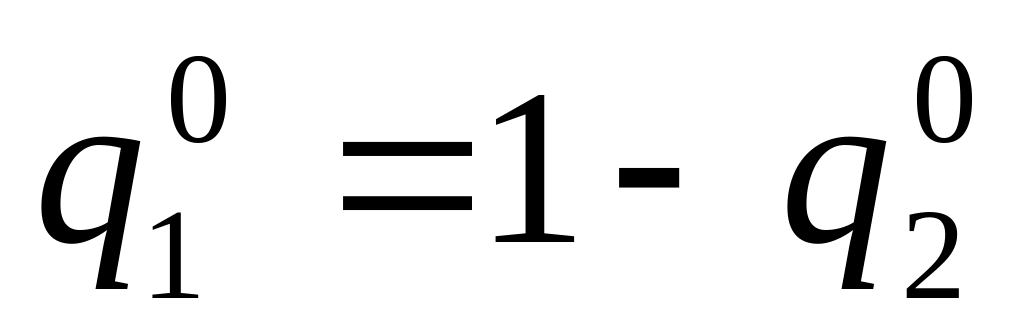Оптимальная смешанная стратегия игрока :
.
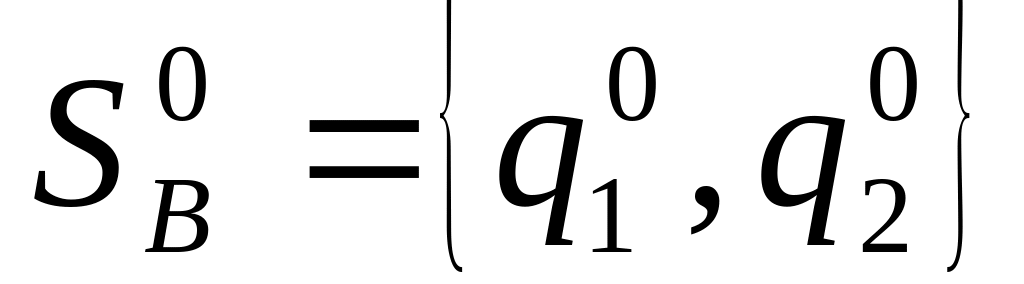Находим
уравнение прямой
,
проходящей через точки
и
:
.
Уравнение
прямой
,
проходящей через точки
и
:
.
Координаты точки :
.
Следовательно,
,
.
Цена игры:
=
.
Оптимальная смешанная стратегия игрока :
.
Полное решение игры:
,
,
.