
Раздел Теория игр
Максимум функции
![]() (*)
(*)
проще всего найти, построив ее график. Для этого поступают следующим образом.
Предположим,
что игрок
![]() выбрал смешанную стратегию
выбрал смешанную стратегию
![]() ,
а игрок
,
а игрок
![]() ―
―![]() чистую стратегию,
чистую стратегию,
![]() .
Тогда средний выигрыш игрока
в ситуации
.
Тогда средний выигрыш игрока
в ситуации
![]() оказывается равным
оказывается равным
![]()
![]() .
.
На
плоскости
![]() уравнение
уравнение
![]() описывает прямую. Тем самым каждой
чистой стратегии игрока
на этой плоскости соответствует своя
прямая. Все эти прямые
(
)
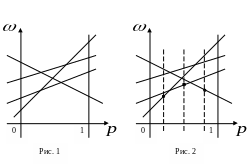
строятся на плоскости
(рис.1). Затем для каждого значения
описывает прямую. Тем самым каждой
чистой стратегии игрока
на этой плоскости соответствует своя
прямая. Все эти прямые
(
)
строятся на плоскости
(рис.1). Затем для каждого значения
![]() ,
,
![]() ,
путем визуального сравнения соответствующих
ему значений
,
путем визуального сравнения соответствующих
ему значений
![]() на каждой из построенных прямых
определяется и отмечается наименьшее
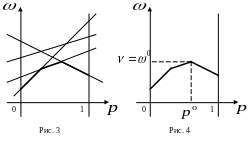
из них (рис.2). В результате описанной
процедуры получается ломаная, которая
и является графиком функции (*) (жирная
линия на рис.3).
на каждой из построенных прямых
определяется и отмечается наименьшее
из них (рис.2). В результате описанной
процедуры получается ломаная, которая
и является графиком функции (*) (жирная
линия на рис.3).
Эта ломаная как бы огибает снизу все семейство построенных прямых, поэтому ее принято называть нижней огибающей этого семейства.
Верхняя
точка построенной нижней огибающей
определяет и цену игры
![]() ,
и оптимальную стратегию игрока
,
и оптимальную стратегию игрока
![]() (рис.4).
(рис.4).
Пример
3.
Найти оптимальные смешанные стратегии
игроков и цену игры, заданной платежной
матрицей
![]() ,
методом нижней огибающей.
,
методом нижней огибающей.
![]() .
.
Решение.
1 шаг. Анализ игры на наличие седловой точки.
|
|
|
|
|
|
-1
|
|
-2 |
|
||
|
6 4 3 1 5 4 |
|
|
|
|
|
|
Седловой точки нет. Решение игры нужно искать в смешанных стратегиях.
2 шаг. Вычисление средних выигрышей игрока (проводится при условии, что игрок выбирает только чистые стратегии).
Из таблицы
|
6 |
4 |
3 |
1 |
-1 |
0 |
|
-2 |
-1 |
1 |
0 |
5 |
4 |
находим средние выигрыши:
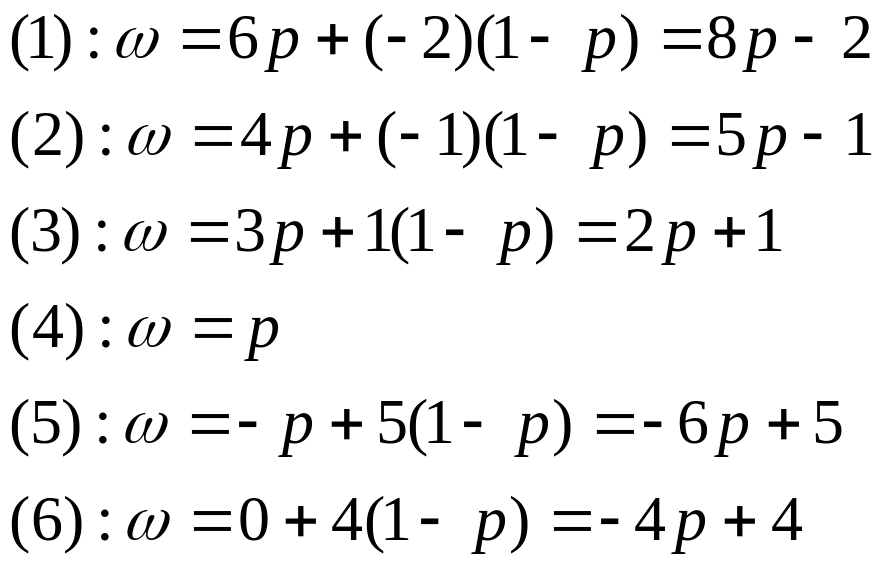
3 шаг. Построение нижней огибающей. Строим на координатной плоскости все шесть прямых, уравнения которых получены на 2 шаге (рис.5, масштаб по осям разный), и находим их нижнюю огибающую.

4 шаг. Определение цены игры и оптимальной смешанной стратегии игрока .
Цену
игры
и оптимальную стратегию игрока
определяет верхняя точка нижней
огибающей. Она лежит на пересечении (4)
и (5) прямых, заданных уравнениями
![]() и
и
![]() (рис.6).
(рис.6).
Решаем систему уравнений:
|
![]() можно
найти из любого уравнения системы
(например, из 1-го).
можно
найти из любого уравнения системы
(например, из 1-го).
Получаем:
![]() =
–
цена игры,
=
–
цена игры,
=![]() –
оптимальная смешанная стратегия игрока
.
–
оптимальная смешанная стратегия игрока
.
5 шаг.
Определение
оптимальной
смешанной стратегии игрока
:
![]() .
.
Полагаем: |
|
|
Из
шести чистых стратегий игрока
выделяем только две:
|
Приравниваем любой из двух средних выигрышей игрока , отвечающий предложенной смешанной стратегии
0 |
0 |
0 |
|
|
0 |
6 |
4 |
3 |
1 |
-1 |
0 |
-2 |
-1 |
1 |
0 |
5 |
4 |
к цене игры:
![]()
![]()
![]() ;
;
или
![]()
![]() .
.
В
обоих случаях получаем, что
![]() .
.
![]() –
оптимальная
смешанная стратегия игрока
.
–
оптимальная
смешанная стратегия игрока
.
Полное решение игры:
![]() =
,
=
,
![]() ,
,
![]() .
.
Метод верхней огибающей
Методом
верхней огибающей находят решение игр
размерностью
![]() .
В этом случае игрок
имеет две чистые стратегии,
а число
чистых стратегий у игрока
произвольно (равно
.
В этом случае игрок
имеет две чистые стратегии,
а число
чистых стратегий у игрока
произвольно (равно
![]() ).
).
Платежная матрица – игры имеет вид:
![]()
Решение
такой игры во многом напоминает решение
![]() -
игры.
-
игры.
Пусть
![]() – произвольная смешанная стратегия
игрока
.
Если игрок
выбирает
– произвольная смешанная стратегия
игрока
.
Если игрок
выбирает
![]() ю
чистую стратегию,
ю
чистую стратегию,
![]() ,
то средний выигрыш игрока
в ситуации
,
то средний выигрыш игрока
в ситуации
![]() будет равным
будет равным
![]() ,
. (**)
,
. (**)
Зависимость этого выигрыша от переменной описывается прямой.
Графиком
функции
![]() является верхняя
огибающая
семейства прямых (**), соответствующих
чистым стратегиям игрока
(рис. 7).
является верхняя
огибающая
семейства прямых (**), соответствующих
чистым стратегиям игрока
(рис. 7).
Абсциссой
нижней точки полученной ломаной будет
значение
![]() ,
определяющее оптимальную смешанную
стратегию игрока
,
а ординатой
–
цена игры
.
,
определяющее оптимальную смешанную
стратегию игрока
,
а ординатой
–
цена игры
.

Отыскание оптимальной смешанной стратегии игрока проводится по той же схеме, которая позволяет находить оптимальную смешанную стратегию игрока в игре .
Пример
4.
Дана платежная матрица
![]() –
игры. Найти цену игры и оптимальные
смешанные стратегии игроков
и
:
–
игры. Найти цену игры и оптимальные
смешанные стратегии игроков
и
:
![]()
Решение.
1 Шаг. Анализ игры на наличие седловой точки.
-
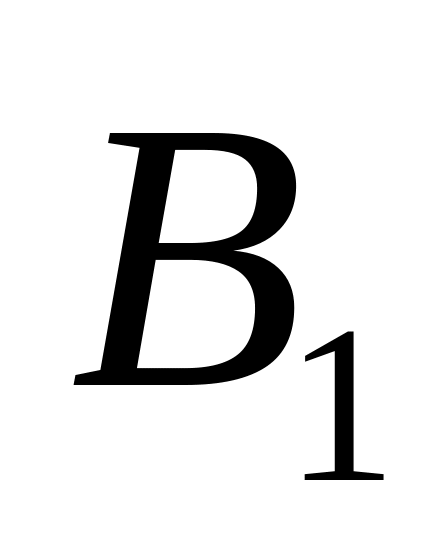
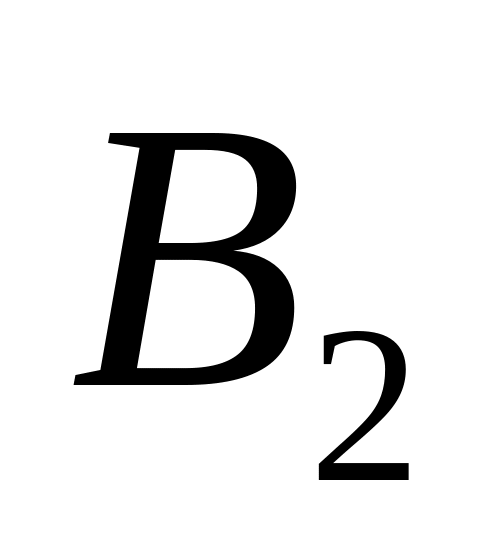

-1

-1

0
3 3

Седловой точки нет. Решение игры нужно искать в смешанных стратегиях.
2 Шаг. Вычисление средних выигрышей игрока (проводится при условии, что игрок выбирает только чистые стратегии).
Из таблицы
|
|
3 |
-1 |
-1 |
3 |
1 |
0 |
находим средние выигрыши игрока :
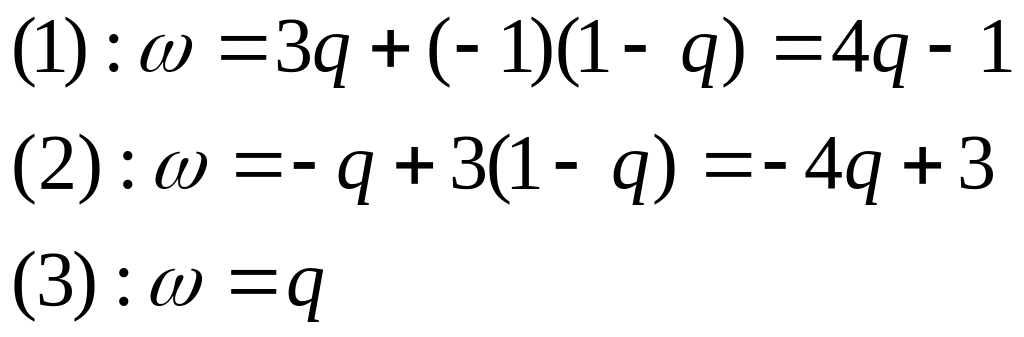
3 шаг. Построение верхней огибающей.
Строим
на координатной плоскости
![]() все три
прямые, уравнения которых получены на
2 шаге и находим их верхнюю огибающую
(рис. 8).
все три
прямые, уравнения которых получены на
2 шаге и находим их верхнюю огибающую
(рис. 8).
(2)
(3)
(1)
0
Рис. 8
1




4 шаг. Определение цены игры и оптимальной смешанной стратегии игрока .
Нижняя
точка верхней огибающей является точкой
пересечения прямых (1) и (2), заданных
уравнениями
![]() и
и
![]() (рис. 8).
(рис. 8).
Решаем систему уравнений:
![]()
![]()
![]()
![]() .
.
![]() =
–
цена игры;
=
–
цена игры;
![]() =
=![]() –
оптимальная смешанная стратегия игрока
.
–
оптимальная смешанная стратегия игрока
.
5 шаг.
Определение
оптимальной
смешанной стратегии игрока
:
![]() .
.
Полагаем:
![]() ,
,
![]() ,
,
![]() (из трех чистых стратегий выделяем
только две –
и
,
соответствующие прямым (1) и (2), которые
пересекаются в нижней точке верхней
огибающей).
(из трех чистых стратегий выделяем
только две –
и
,
соответствующие прямым (1) и (2), которые
пересекаются в нижней точке верхней
огибающей).
Из таблицы
-
3
-1
-1
3
0
1
0
находим средние выигрыши игрока . Для этого приравниваем средние выигрыши игрока , соответствующие чистым стратегиям игрока :
![]()
![]()
![]() .
.
Таким
образом, оптимальная смешанная стратегия
игрока
:
![]() .
.
Полное решение игры:
![]() ,
,
![]() ,
,
![]() .
.
