4.Коэффициент вариации (V)

V = 2,49 : 5,2 = 0,48

0,48 * 100 % = 48 %

Таким образом, по своему составу совокупность неоднородна так как коэффициент вариации более 33 % .

5.Мода (Mo)

Мода (Мо) – значение признака, наиболее часто встречающееся в исследуемой совокупности, то есть это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту. В интервальном ряду по наибольшей частоте определяется модальный интервал, а конкретное значение моды в интервале вычисляется по формуле: Мо= ,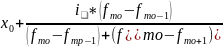

где Хо и i – соответственно нижняя граница и величина модального интервала;

, – частоты модального, предмодального и послемодального интервалов.

Таблица 3

Количество авто	7	6	6	4	6	6	4	11
S (накопленные частоты)	7	13	19	23	29	35	39	50

N=(50+1)/2=25.5

Выбираем интервал , так как его накопленная частота наиболее приближена к .

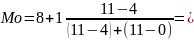
6.Медиана (Ме)

Медиана (Ме) – значение признака, приходящиеся а середину ранжированной совокупности, то есть это вариант, который делит ряд распределения на две равные по объёму части.

Медиана, как и мода, не зависит от крайних значений вариантов, поэтому применяется для характеристики центра в ряду распределения с неопределёнными границами.

Для определения медианы в ранжированном ряду необходимо вначале найти номер медианы: N=(n+1)/2

N=(50+1)/2=25.5

В случае интервального вариационного ряда распределения конкретное значение медианы вычисляется по формуле:

Ме= ,

где Хо и i – соответственно нижняя граница и величина модального интервала;

fме – частота медианного интервала;

S_ме-1-кумулятивная частота предметного интервала.

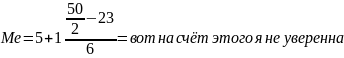
7.Эксцесс (Ek)

Для определения крутизны графика распределения в качестве эталонного выбирается нормальное распределение, которое сравнивается с фактическим и вычисляется показатель эксцесса распределения:

Найдём центральный момент четвёртого порядка:

µ4= = ((1,5-5,2)⁴ *7+(2,5 -5,2)⁴ *6 +(3,5 -5,2)⁴*6+(4,5 -5,2)⁴ *4 +(5,5 - 5,2)⁴ *6+(6,5-5,2)⁴*6+(7,5-5,2)⁴*4+(8,5-5,2)⁴*11)/50=(187,42⁴+53,14⁴+8,35⁴+0,24⁴+0,01⁴+2,56⁴+27,98⁴+118,59⁴):50=

3115,5/50=62,31

Ex=62,31