Программное обеспечение

Программное обеспечение - это совокупность программ, необходимых для обработки исходной информации по проектным алгоритмам, управление вычислительным процессом, организацией хранения и вывода данных.

• Общее программное обеспечение предназначено для совершенствования процесса проектирования (СУБД, математические, графические системы)

• Специальное программное обеспечение предназначено для выполнения проектных операций и процедур

Оптимизация в сапр Роль оптимизации в сапр. Виды оптимизации

Одной из главных задач в САПР является получение оптимальных решение (оптимизация).

Основным требованием проектных решений является их практическая приемлемость и рациональность.

Практическая приемлемость это возможность реализации в конкретных производственных условиях. Для этого разрабатывается система ограничений на решение.

Рациональность – получение наилучших технико-экономических показателей. Для этого определяется критерий оптимальности.

Для постановки задач оптимизации необходимо разработать математическую модель, которая включает в себя:

1. Переменные – это параметры, оптимальное значение которых надо найти

2. Параметры – постоянные величины

3. Система ограничений – совокупность математических объектов, определяющих область допустимых значений переменных

4. Функция цели (целевая) – математическое выражение, связывающее критерии оптимальности с переменными.

Оптимальное решение – решение, обеспечивающее условия:

1. выполнение системы ограничений

2. доставление экстремума к критерию оптимальности

Этапы решения задач оптимизации:

1. Определить переменные и выбрать критерии оптимальности

2. Составить систему ограничений

3. Записать функцию цели

4. Разработать метод решения

Основные виды оптимизации:

• параметрическая

• структурная

Различия между ними заключается в сущности переменных. В параметрической оптимизации переменные представляют собой упорядоченное множество. При структурно – переменные представляют собой неупорядоченное множество.

Параметрическая оптимизация

Пример: Расчет оптимальных режимов резания.

1. Переменными будут являться подача инструмента S, число оборотов шпинделя станка(n), время обработки

2. В качестве ограничений возьмем точность обработки, чистоту поверхности (шероховатость), стойкость инструмента, технологические возможности станка (мощность электродвигателя, пределы чисел оборотов и подач)

3. Функция цели:

Методы решения:

• Аналитический метод – решение известными методами. Основным недостатком метода в данной задаче является то, что переменные рассматриваются как непрерывные величины, поэтому возникает проблема округления их до дискретного значения.

• Алгоритмический метод – использует свойства дискретности непрерывных величин. Например, число оборотов n на станке известны их все дискретные значения, поэтому, последовательно подставляя эти известные значения в систему ограничений, получим систему неравенств с одним неизвестным. Найденное значение S подставляем в функцию цели. Таким образом, мы получим ряд значений функций целей. И выбираем максимальное значение, по которому определим оптимальное значение.

• Геометрический метод – решается на плоскости координат S и n. Для упрощения решений систему уравнений необходимо привести к линейной, для этого прологарифмируем:

Теперь решим эту задачу на плоскости lnS, lnn

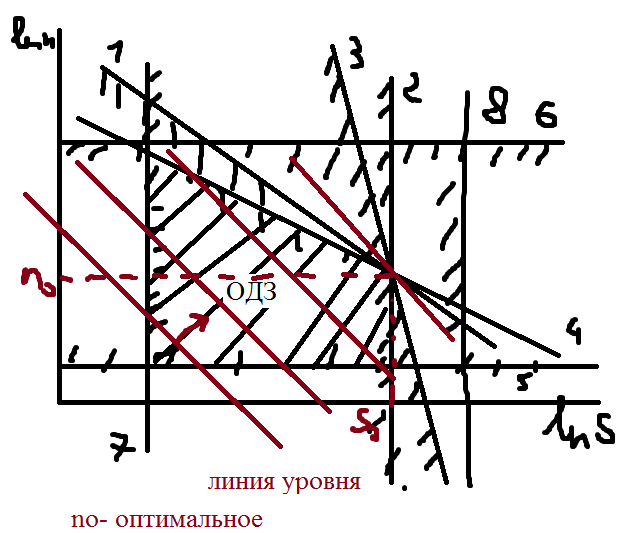
Прологарифмируем функцию цели:

Функция цели представляет собой плоскость в координатах ln n, ln S, ln F. Пересечение этой плоскости с плоскостью координат lnn, lnS дает прямую линию, которая называется линия уровня. Если функция цели стремится к максимуму, то линия уровня будет перемещаться параллельно сама себе в сторону от начала координат. Если к минимуму, то к началу координат. Точка ОДЗ которую линия уровня коснется последней и будет оптимальной. Для построения лини уровня достаточно ln F прировнять к какому то числу и по точкам построить линию уровня.