Лекция 9.Алгебра случайных величин. 2.11.12

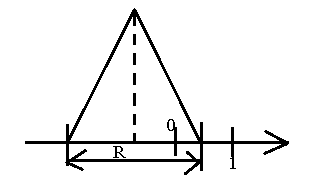
Алгебра случайных величин нужна для исчислений (мат ожиданий и СКО).

1. А)

Конкуренты мат ожидания – медиана med(X) и мода mod(X).

Мода случайной величины это точка в которой достигается максимум плотности.

Б) Если Х,Y - независимые, то M(XY)=M(X)*M(Y)

2. В расчетах вместо СКО применяют ковариациии дисперсии.

центрированные случайные величины

Дисперсия

Если X, Y– независимые, то

А) M(const)=const

Б)

B)

Г)

Лекция 10. Примеры вычисления мат ожидания, медианы, моды, дисперсии и ско. 9.11.12

1)

Х	-1	0	2
Р	1/6	2/6	3/6

По 2 известным определить следующее – это экстраполяция.

P

Лекция 11. Система случайных величин (Многомерная с.В.). 16.11.12

Пример Пробой мишени

Реализация с.в.

Для описания взаимосвязи XY и, в конечном счете, для описания рассеивания случайной величины V используют ковариацию .

Ковариационная матрица с.в. X,Y:

Неравенство Коши-Буняковского-Шварца

(1)

Крайние случаи:

Коэффициент корреляции

Теорема. Если X,Y– независимые случайные величины, то

Обратное вообще говоря неверно.

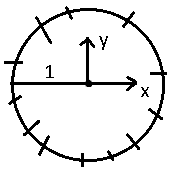
Говорят

Этот пример показывает, что могут быть некоррелированныес.в., но функционально зависимые.

Опр.

X	41	42	43	45
P	0,3	0,3	0,2	0,2

Лекция 23.11.12

Раздел 2. Математическая статистика

h=3 объём выборки

– генеральная совокупность

Х

Единственный способ востановить случайную величину по генеральной совокупности это выборочный метод.

Аналог функции распределения в МС - выборочная функция распределения или эмпирическая функция распределения.

Для удобства использую первоначальную сортировку выборки.

-2
11
5
1
1
7
8
3

Лекция 13. 30.11.12. Датчик случайных чисел.

Мультипликативный датчик

Д. Кнут «Искусство программирования» Т. Целочисленная арифметика.

а=4 b=0

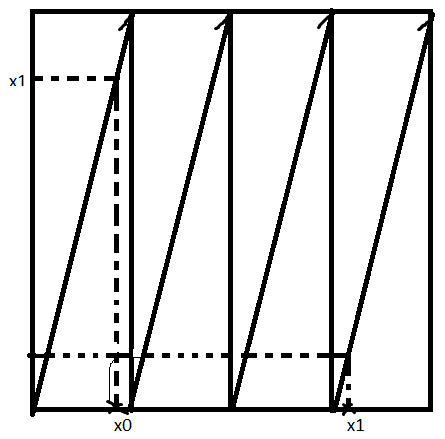
Нормальные «случайные» числа

Применение датчиков случайных числе называется методом монтекарло

Лекция 14. 7.12.12

Теория вероятности	Математическая статистика
С.В. X	Ч.С.
Ф. распределения Плотность F	Эмпирическая функция распределения|Гистограмма, Полигон

Пусть есть выборка объёма n.Если её отсортировать получить вариационный ряд.

Для построения гистограммы n должно быть достаточно большим.

Исходя из величины n берем m – число промежутков.

Если бы

То

Частости попадания на так расположенные промежутки образуют гистограмму (столбики) или полигон (ломаная).

Чем промежуток уже тем информации теряется меньше.

Каким брать шаг. Пусть

Центры промежутков:

-2
11
5
1
1
7
8
3