Лекция 6.Распределение случайный величин.12.10.12

В n,р	0	1	…	M	...	n
Р

p-вероятность успеха в 1 испытании.

n – общеечисло испытаний.

Определение дискретного распределения (дискретная случайная величина задается таблицей распределения).

X			…
P			…

П.2. Распределение Пуассона.

	0	1	…	m	…
Р

Т. (Пуассон).

Если , а , то

Эту теорему часто называют теорема о редких событиях

Жертв ДТП в ковровском районе в среднем 5.

Пример.

n>>10

Равномерное распределение.

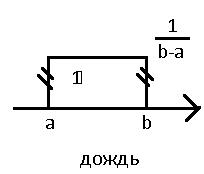
Нормальное распределение (гауссовское)

а – центр расспределения

Лекция 7 Характеристики случайных величин

Для дискретной случайной величины это функция будет иметь ступенчатый график.

X
P	0,2	0,3	0,15	0,35

Если Х – это непрерывно распределенная случайная величина (равномерное, нормальное и т.д.).

Аналогом таблицы распределения становится плотность

Для дискретной случайной величины исчерпывающие характеристики функции распределения и таблица распределения. И для непрерывно распределенной случайной величины исчерпывающие характеристики функция распределения и плотность распределения.

Главные параметры с.в.

1. Центр рассеивания. Если распределения симметрично, то центр рассеивания совпадает с центром симметрии. Наиболее популярное формальное определение центра рассеивания – это математическое ожидание:

Так же для формализации центра рассеивания используется медиан

Медиан – это такая точка левее которой оказаться вероятность равна 50% и правее 50%.

Мат ожидание это точный аналог центра масс.

Мера рассеивания.

Среднеквадратическое отклонение (СКО)

Для дискретного распределения:

Т.

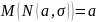
Правило 2 сигм.

1. Находят размах R расс.

2. 

Лекция 8. Асимптотические (предельные) теоремы т. Вероятности. 26.10.12

Пример:

Самая знаменитая асимптотическая теорема является центральная предельная теорема (ЦПТ).

Сумму большого числа независимых случайных величин, среди которых нет доминирующих, распределена приблизительно по нормальному закону.

N – Нормально распределенная случайная величина.

Применения:

1. Артиллерия и т.п.

2. Метрология и т.п.

3. И т.д.

История ЦПТ:

1. Лаплас, Муавр

2. Гаусс

3. Ляпунов (уч.Чебышёва).

Частный случай 1)

	0	1
		1/2

	0	1
		1/2

При n>>1

Муавр-Лаплас

q=1-p

N(0,1)

Опр. Х центрируется: х-а

Нормируется:

Если производится Nнезависимых испытания с вероятностью успеха p в каждом, то это схема Бернулли.

Задача 20.