Лекция 2. Аксиома теории вероятности. 14.09.12
-невозможное
событие
Е – достоверное событие
Аксиома сложения. Если событие А и В несовместны, т.е. A*B= , то P(A+B)=P(A)+P(B).
Эквивалентное
выражение. P(A+B)=P(A)+P(B)-P(AB)
Пример «Лужа»
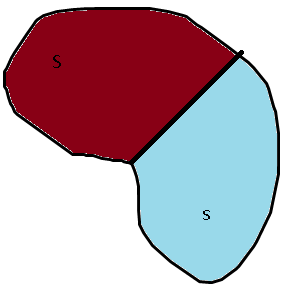
Пример
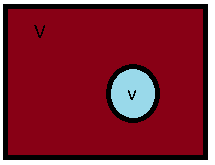
При условии объективной симметрии возможно априорное назначение вероятности.
На этом построена формула классического определения вероятности. В отсутствии объективной симметрии, начальная назначение вероятности возможно только статистическим методом.
Где n – число испытаний
m
– число успехов
Это формула не совершена потому что при одной серии испытаний получим одно число а при другой серии испытаний получим другое число.
Пример Вероятность поражения цели ракетой.
Закон больших чисел. В случае объективной симметрии статистическая вероятность (апостериорная) стремится к априорной при увеличении числа оппытов.
Априорная формула Бюффона
1733 год.
Экспериментальным подтверждением зааконов больших чисел служит опыт Бюффона и опыты с монеткой
РГР задача 2
1-5 7-9 .12, 13, 15, 17, 19-21,33
Лекция 3. Вероятность «произведения» событий. 21.09.12
A,B,C,… – события .
A+B
A*B
Теорема:
Если события независимы
Задача имени В. Теркина.
n~10000
p≈0
P=?
«Хотя бы один».
В этом случае отталкиваемся от противоположного события: не один.
Ответ:
Условная вероятность
B при условии A.
Теорема:
Если событие A и Bнезависимы то
P(B/A)=P(B)
P(A/B)=P(A)
Задача 8
В двух партиях k1 и k2 % доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них: a) хотябы одно бракованное б) два бракованных в) одно доброкачественное и одно бракованное?.
К1=79
К2=38
Задача 9
Вероятность того что цель поражена при одном выстреле первым стрелком p1, вторым- p2. Первый сделал n1 второй n2 выстрелов. Определить вероятность того что цель не поражена.
Лекция 5.Формула Якоба Бернули. 5.10.12
Семантика – это содержание, которое строится за каждым термином.
Я. Бернули ≈ 1696.
Производится n опытов в каждом вероятности успеха p.
Какова вероятность получиться m успехов.
Ответ:
N=5
M=0…5
P=0,5
|
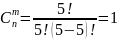
0,15625 |
0,3125 |
0,3125 |
0,15625 |
0,03125 |
|
|
|
|
m 0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,03125