Лекция 1. Основные понятия. 7.09.12

1. Ферма (карты, 1 половина 17 века).

2. Страховое дело (1 половина 17 века).

3. Якоб Бернулли.

Закон больших числе – если мерить долго одно и тоже то в среднем получим именно это.

100 Павловский А.Ф. (ученик Осиповский) 1821г.

Пример: Вероятность встретить блондинку.

Подходы: в группе (выборка) выборочная частота. P≈0,12частость результат выборочного метода.

Классическое определение вероятности (комбинаторное)

N – число вариантов (всех событий).

M – числоблагоприятствующих.

Чудесенко РГР. Номер 5.

Практика

Определить вероятность того что

a)сумма очков не превосходит N

b)произведение числа очков не превосходит N

c) Произведение числа очков делится N.

N=7.

a)

	1	2	3	4	5	6
1	X	X	x	x	x	X
2	X	x	x	x	X
3	x	x	x	X
4	X	x	x
5	X	X
6	x

b)

	1	2	3	4	5	6
1	X	X	X	X	X	X
2	X	X	X
3	X	X
4	X
5	X
6	X

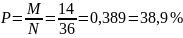
c)

	1	2	3	4	5	6
1
2
3
4
5
6

Задача 2.

Имеются изделия 4 сортов причем число изделий i-го сорта равно n_i, i=1,2,3,4. Для контроля наудачу берутся m изделий. Определить вероятность того, что среди них m₁ первосортных,m₂, m₃, m₄ соответственно.

N₁=4

N₂=2

N₃=2

N₄=2

M₁=3

M₂=1

M₃=2

M₄=1