3.1.4.3. Движение заряженных частиц в магнитном и электрическом полях

а) Движение заряженных частиц в однородном магнитном поле

Пусть положительно заряженная частица q движется со скоростью перпендикулярно ( ) силовым линиям магнитного поля. Найти частоту, период обращения частицы и радиус R кривизны траектории (рис.160). Сила Лоренца, действующая на частицу, равна

Fл= qVB

(378)

т.к. , .

По закону Ньютона ma=qVB, где - центростремительное ускорение. Тогда

,

откуда получим формулу радиуса кривизны:

.

(379)

Период обращения частицы равен

,

(380)

где – длина окружности траектории частицы.

Циклическая частота равна

и называется циклоторонной.

(381)

Пусть положительно заряженная частица влетает в однородное магнитное поле под углом α к силовым линиям (рис. 161). Скорость частицы можно разложить на параллельно и перпендикулярно силовым линиям. На частицу будет действовать сила Лоренца

Рис.161

и она будет совершать вращательное и поступательное движения (за счет ). Следовательно она будет двигаться по винтовой траектории. Определим шаг винта и радиус R кривизны траектории. Так как период обращения не зависит от скорости, то используя формулу (381) найдем радиус.

(382)

где .

Шаг винта, т.е. расстояние, пройденное частицей q за один период, с учетом (382) и (380) определяется формулой

(383)

где .

Движение заряженной частицы в ограниченном пространстве магнитного поля

Дано ограниченное пространство магнитного поля размерами (рис.162), силовые линии которого направлены перпендикулярно плоскости чертежа от нас.

На расстоянии l₂ от границы магнитного поля находится экран. Нужно найти отклонение (Y) частицы от прямолинейной траектории, если частица влетает в магнитное поле со скоростью V₀ перпендикулярно к силовым линиям.

Из рис. 162 видно, что

Y=Y1+Y2

(384)

Движение частицы в магнитном поле вдоль оси Х является равномерным и поэтому

l1=V0t

(385)

Вдоль оси Y на частицу действует сила Лоренца, поэтому она будет двигаться с ускорением

Рис.162

(386)

Поэтому и с учетом (385) и (386) получим

.

(387)

Из треугольника АCР следует, что

.	(388)
Т.к ,	(389)

то (388) получим

.

(390)

Подставляя (387) и (390) в (384) получим

.

(391)

б) Движение заряженных частиц в электрическом поле

Пусть однородное электрическое поле создано плоским воздушным конденсатором размерами: l₁ - длина обкладок конденсатора, d – расстояние межу обкладками (рис.163). На расстоянии l₂ от концов пластин конденсатора находится экран. К пластинам приложена разность потенциалов, которая создает однородное электрическое поле, направленное от верхней к нижней пластинам (рис.163). Перпендикулярно к силовым линиям влетает положительно заряженная части q.

Нужно найти отклонение частиц от прямолинейной траектории, т.е

ОР=Х=Х1+Х2

(392)

Движение частицы вдоль оси Y является равномерным прямолинейным, т.к. на нее не действуют силы в этом направлении. Поэтому

l1=V0t	(393)
Рис.163

Вдоль оси X на частицу действует электрическая сила F_e=qE и движение ускоренное. Поэтому

. (394)

По второму закону Ньютона ma=qE и

. (395)

С учетом (393) и (395) получим

.

(396)

Из треугольника ACP следует

или .

(397)

Скорость частицы вдоль оси У равна

. (398)

С учетом (398) формула (397) запишется в виде

.

(399)

Тогда с учетом (396) и (399) окончательно отклонение равно (392)

.

(400)

в) Движение заряженных частиц в магнитном и электрическом полях

Пусть заряженная частица движется в ограниченном пространстве однородных, сонаправленных электрического и магнитного полей (рис.164). Параметры пространства указаны в предыдущих пунктах. Найти уравнение траектории частицы.

Рис.164

Так как на частицу действуют электрическая сила и сила Лоренца , которые направлены взаимно перпендикулярно (рис.164), то траекторией движения частицы будет парабола, которая показана на рисунке. Координатами параболы являются (391) и (400).

Решая совместно (391) и (400) получим:

(401)

Из (401) можно найти удельный заряд любой заряженной частицы:

(402)

Используя метод, описанный выше, формулу (402) впервые получил Томсон в 1907г и назывался “методом параболы”. Используя этот метод он обнаружил два изотопа неона. В дальнейшем этот метод усовершенствовал Астон и создал прибор масс-спектрограф, используемый для исследования химического состава любого вещества. Методы использования подробно описаны в книгах И.В.Савельева “Электричество и магнетизм”, 2008г стр.247-268.
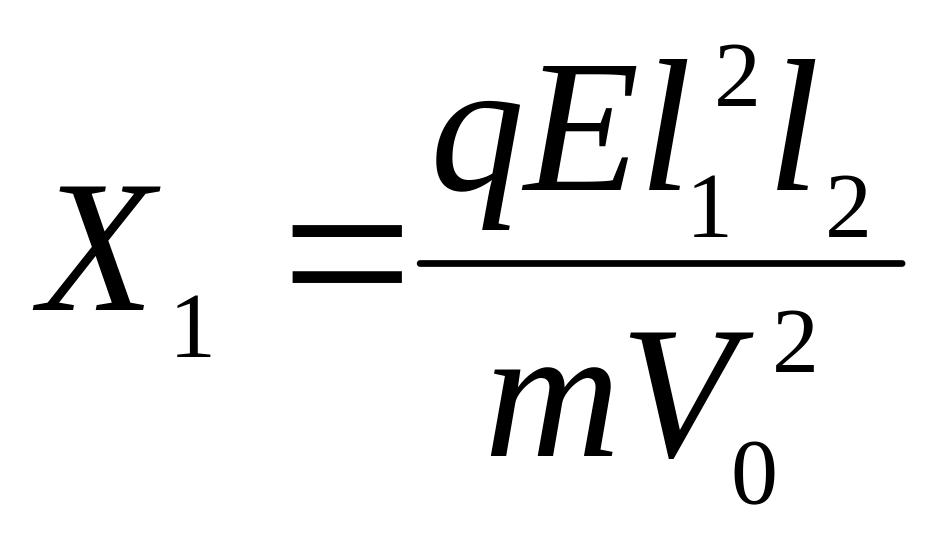