Критерии оценки

№	Критерий	Описание
1	Атака	Сила наносимого урона противнику
2	Защитные характеристики	Способность к выживанию. Включает в себя защиту, способность к уклонению от атак противника, профессиональные умения, позволяющие выжить.
3	Интересность	Без интереса нет смысла играть
4	Полезность в сражении	Ваша польза союзникам в сражениях.
5	Полезность при фарме ПБ	Ваша польза союзникам при попытке убить пит босса.
6	Способность качаться	Способность быстро и легко прокачивать своего персонажа, повышая его уровень мастерства.

3. Определение лингвистических оценок

Не всегда возможно оперировать точными количественными характеристиками, поэтому важно иметь однозначно доступные и достаточно удобные способы оценки риска. В методе Делфи для решения этой проблемы используются так называемые лингвистические термы (оценки).

В моей работе данную предметную область исследуют 4 эксперта. В результате, эксперт заключает одну из пяти лингвистических оценок для каждого критерия по каждой альтернативе:

• Очень хорошо (VG - Very Good)

• Хорошо (G - good)

• Средне (N - Normal)

• Плохо (B - Bad)

• Очень плохо (VB - Very Bad)

Для математического описания лингвистических переменных воспользуемся аппаратом теории нечётких множеств. Элемент обычного (чёткого) множества определяется либо однозначно принадлежностью, либо непринадлежностью к тому или иному множеству. Иными словами функция принадлежности может принимать лишь два значения:

• 1 – в случае, если элемент принадлежит данному множеству

• 0 – в случае, когда элемент не принадлежит данному множеству

А элемент нечёткого множества может принимать значения на интервале от нуля до единицы.

Для описания нашей ситуации возьмем нечёткие множества такого типа, функция принадлежности которых может быть описана в виде трапеции (трапециевидная функция принадлежности). К примеру, функция принадлежности такого множества может выглядеть следующим образом:

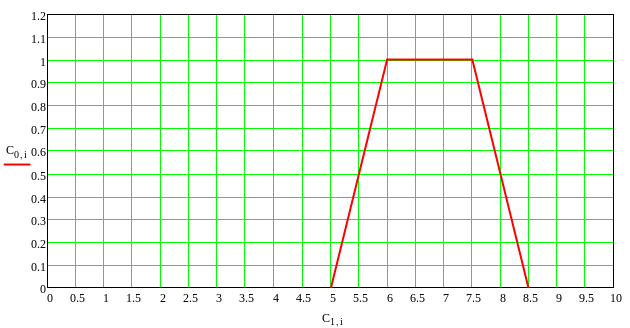
Трапециевидная функция принадлежности может иметь разные длины боковых сторон. Из графика видно, что на интервале [5; 8.5] функция принимает значение 1, лежащие на этом интервале точки однозначно принадлежат данному множеству. Этот интервал называется интервалом правдоподобия. На интервалах [5; 6] и [7.5; 8.5] функция принадлежности принимает ряд значений от 0 до 1, эти интервалы называются интервалами неуверенности. Значения функции принадлежности, находящиеся между нулём и единицей, выражают степень нашей неуверенности в принадлежности того или иного элемента множеству. И чем меньше значение функции принадлежности, тем больше неуверенность в принадлежности элемента множеству.

Нечёткое множество, например, назовём его A, также обозначается следующим образом:

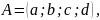
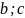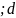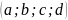где [ ] – интервал правдоподобия, [ ] – левый интервал неуверенности, [c ] – правый интервал неуверенности. Функция принадлежности обозначается , для нашего примера

К примеру, множество, функция принадлежности которого изображена на иллюстрации выше, обозначается следующим образом: (2; 4; 6; 8), где [2; 4] – левый интервал неуверенности, [4; 6] – интервал правдоподобия множества, [6; 8] – правый интервал неуверенности.