. Задача № 3. Расчет переходного процесса с источником произвольной формы интегралом Дюамеля
Для получения расчетной схемы необходимо в топологию цепи (рис. 1) поместить элементы из табл. 1 согласно варианту, которые указаны буквами. Если в табл. 1 элементы записаны через запятую, то они включаются в ветвь последовательно, а если через знак //, то элементы соединены параллельно. Направление источников должно совпадать с направлением, указанным в ветвях топологической схемы (рис. 1). Если перед Е или J стоит знак минус, то направление источников направлено в противоположную сторону.
Вариант задается преподавателем или определяется по последним двум цифрам зачетной книжки (студенческого билета).
Рекомендуется следующий порядок расчёта переходного процесса в цепях, на вход которых подаётся возмущение произвольной формы:
определяется переходная функция расчётом переходного процесса в цепи, коммутируемой на единичный источник энергии. Если необходимо рассчитать ток в ветви схемы, определяется
,
если же нужно рассчитывать напряжение
на зажимах ветви или элементах схемы,
то определяется
.
Если на вход цепи подаётся напряжение
произвольной формы, то переходная
функция определяется при включении
этой цепи на постоянное напряжение,
равное 1 В.
Если же на вход заданной цепи подаётся
ток произвольной формы, то переходная
функция рассчитывается при включении
цепи на источник постоянного тока,
равного 1 А;выполняется кусочно-линейная аппроксимация входного сигнала произвольной формы;
осуществляется аналитическая запись воздействующей функции напряжения или тока с указанием интервалов времени для каждого аналитического выражения. Границы интервалов определяются либо моментами времени, когда воздействующая функция изменяется скачком, либо теми моментами времени, когда воздействующая функция меняет закон изменения во времени;
осуществляется поинтервальный расчёт искомого тока или напряжения при помощи интеграла Дюамеля.
выполнить расчет схемы в программе MATHCADи измерить токи во всех ветвях и напряжения во всех узлах и привести протокол моделирования;
выполнить моделирование схемы в программеMATLAB ИSIMULINKи измерить токи во всех ветвях и напряжения во всех узлах и привести протокол моделирования;
сравнить результаты расчета и моделирования.
Назначение букв в таблице следующее: |
|
Численное значение элементов для всех вариантов равно: |
Е - постоянный источника ЭДС |
|
Е = 100 B |
J - постоянный источника тока |
|
J = 2 A |
R - сопротивление |
|
R = 100 Ом |
L– индуктивность |
|
L = 0,05 Гн |
C– емкость |
|
C = 1,0 мкФ |
0- проводник |
|
|
Таблица 1
Вариант |
Номер ветви |
Вид источников |
Найти |
|||||||||
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
||
|
|
E,R |
R |
L |
C |
0 |
R |
R |
R |
1 |
iL(t) |
||
|
|
C |
R |
0 |
L |
R |
R |
R |
J |
2 |
uC(t) |
||
|
|
R |
E,R |
C |
L |
0 |
L |
R |
R |
3 |
iL(t) |
||
|
|
L |
R |
0 |
R |
R |
R |
J |
C |
4 |
uC(t) |
||
|
|
R |
R |
E,R |
C |
L |
R |
0 |
R |
5 |
iL(t) |
||
|
|
R |
L |
R |
E,R |
R |
J |
C |
0 |
6 |
uC(t) |
||
|
|
R |
J |
R |
E,R |
C |
R |
L |
0 |
7 |
iL(t) |
||
|
|
L |
R |
E,R |
R |
J |
C |
0 |
R |
8 |
uC(t) |
||
|
|
L |
R |
J |
R |
E,R |
0 |
R |
C |
9 |
iL(t) |
||
|
|
R |
E,R |
R |
J |
C |
0 |
R |
L |
10 |
uC(t) |
||
|
|
0 |
L |
R |
J |
R |
E,R |
C |
R |
11 |
iL(t) |
||
|
|
E,R |
R |
J |
C |
R |
0 |
L |
R |
12 |
uC(t) |
||
|
|
L |
R |
0 |
R |
J |
R |
E,R |
C |
13 |
iL(t) |
||
|
|
R |
J |
C |
0 |
R |
L |
R |
Е |
14 |
uC(t) |
||
|
|
C |
R |
0 |
L |
R |
J |
R |
E,R |
15 |
iL(t) |
||
|
|
J |
C |
R |
0 |
L |
R |
E,R |
R |
16 |
uC(t) |
||
|
|
E,R |
R |
C |
R |
O |
L |
J |
R |
17 |
iL(t) |
||
|
|
R |
C |
0 |
R |
L |
E,R |
R |
J |
18 |
uC(t) |
||
|
|
R |
E,R |
R |
R |
L |
C |
0 |
J |
19 |
iL(t) |
||
|
|
C |
0 |
R |
L |
E,R |
R |
J |
R |
20 |
uC(t) |
||
|
|
J |
R |
E,R |
R |
C |
0 |
R |
L |
21 |
iL(t) |
||
|
|
R |
0 |
L |
E,R |
R |
J |
R |
C |
22 |
uC(t) |
||
|
|
L |
J |
R |
E,R |
R |
C |
0 |
R |
23 |
iL(t) |
||
|
|
L |
R |
0 |
E,R |
R |
J |
R |
C |
24 |
uC(t) |
||
|
|
C |
R |
J |
R |
E,R |
R |
0 |
L |
25 |
iL(t) |
||
|
|
R |
L |
E,R |
R |
J |
R |
C |
0 |
26 |
uC(t) |
||
|
|
L |
R |
0 |
J |
R |
E,R |
R |
C |
27 |
iL(t) |
||
|
|
C |
E,R |
R |
J |
R |
0 |
L |
R |
28 |
uC(t) |
||
|
|
0 |
L |
C |
R |
J |
R |
E,R |
R |
29 |
iL(t) |
||
|
|
E,R |
R |
J |
R |
C |
R |
0 |
L |
30 |
uC(t) |
||
|
|
R |
C |
0 |
R |
L |
J |
R |
E,R |
31 |
iL(t) |
||
|
|
J |
R |
0 |
L |
C |
R |
E,R |
R |
32 |
uC(t) |
||
|
|
E,R |
C |
R |
L |
R |
0 |
J |
R |
33 |
iL(t) |
||
|
|
R |
0 |
E,R |
C |
L |
R |
R |
J |
34 |
uC(t) |
||
|
|
R |
E,R |
R |
C |
L |
0 |
R |
J |
35 |
iL(t) |
||
|
|
L |
C |
R |
0 |
R |
E,R |
J |
R |
36 |
uC(t) |
||
|
|
J |
R |
C |
E,R |
R |
L |
0 |
R |
1 |
iL(t) |
||
|
|
C |
R |
J |
R |
E,R |
R |
R |
O |
2 |
uC(t) |
||
|
|
R |
J |
L |
R |
E,R |
0 |
C |
R |
3 |
uC(t) |
||
|
|
L |
R |
C |
E,R |
R |
J |
0 |
R |
4 |
iL(t) |
||
|
|
0 |
R |
C |
J |
R |
E,R |
L |
R |
5 |
iL(t) |
||
|
|
R |
E,R |
L |
R |
J |
C |
R |
0 |
6 |
uC(t) |
||
|
|
0 |
R |
E,R |
R |
J |
R |
C |
L |
7 |
iL(t) |
||
|
|
E,R |
R |
C |
J |
R |
L |
0 |
R |
8 |
uC(t) |
||
|
|
0 |
R |
R |
L |
R |
J |
E,R |
C |
9 |
iL(t) |
||
|
|
R |
J |
L |
0 |
R |
C |
R |
E,R |
10 |
uC(t) |
||
|
|
R |
0 |
J |
C |
L |
R |
R |
E,R |
11 |
iL(t) |
||
|
|
J |
C |
R |
L |
0 |
R |
E,R |
R |
12 |
uC(t) |
||
|
|
E,R |
R |
L |
R |
0 |
C |
J |
R |
13 |
iL(t) |
||
|
|
R |
C |
E,R |
L |
R |
0 |
R |
J |
14 |
uC(t) |
||
|
|
R |
E,R |
0 |
R |
C |
R |
L |
J |
15 |
iL(t) |
||
|
|
C |
0 |
R |
R |
L |
E,R |
J |
R |
16 |
uC(t) |
||
|
|
J |
R |
0 |
-E,R |
R |
C |
R |
L |
17 |
iL(t) |
||
|
|
L |
C |
J |
R |
E,R |
R |
R |
0 |
18 |
uC(t) |
||
|
|
0 |
J |
C |
R |
-E,R |
R |
L |
R |
19 |
iL(t) |
||
|
|
L |
0 |
-J |
R |
E,R |
R |
R |
C |
20 |
uC(t) |
||
|
|
0 |
L |
R |
J |
R |
E,R |
C |
R |
21 |
iL(t) |
||
|
|
C |
L |
R |
-E,R |
R |
J |
R |
0 |
22 |
uC(t) |
||
|
|
R |
0 |
E,R |
L |
J |
R |
R |
C |
23 |
iL(t) |
||
|
|
L |
E,R |
0 |
R |
J |
R |
R |
C |
24 |
uC(t) |
||
|
|
0 |
L |
R |
C |
R |
J |
E,R |
R |
25 |
iL(t) |
||
|
|
E,R |
R |
L |
J |
R |
C |
0 |
R |
26 |
uC(t) |
||
|
|
R |
R |
J |
L |
C |
0 |
R |
E,R |
27 |
iL(t) |
||
|
|
J |
R |
L |
0 |
R |
C |
E,R |
R |
28 |
uC(t) |
||
|
|
R |
L |
-E,R |
C |
0 |
R |
J |
R |
29 |
iL(t) |
||
|
|
L |
R |
C |
0 |
R |
E,R |
R |
J |
30 |
uC(t) |
||
|
|
E,R |
C |
R |
0 |
R |
L |
R |
J |
31 |
iL(t) |
||
|
|
C |
R |
L |
R |
E,R |
R |
J |
0 |
32 |
uC(t) |
||
|
|
R |
E,R |
A |
C |
R |
0 |
L |
R |
33 |
iL(t) |
||
|
|
L |
R |
C |
E,R |
R |
J |
0 |
R |
34 |
uC(t) |
||
|
|
J |
R |
R |
-E,R |
C |
0 |
R |
L |
35 |
iL(t) |
||
|
|
R |
E,R |
L |
R |
J |
R |
0 |
C |
36 |
uC(t) |
||
|
|
R |
-J |
L |
R |
E,R |
C |
R |
0 |
1 |
iL(t) |
||
|
|
E,R |
R |
R |
J |
C |
R |
0 |
L |
2 |
uC(t) |
||
|
|
0 |
R |
C |
J |
R |
E,R |
R |
L |
3 |
iL(t) |
||
|
|
R |
J |
E,R |
C |
R |
0 |
L |
R |
4 |
uC(t) |
||
|
|
C |
R |
L |
R |
J |
R |
E,R |
0 |
5 |
iL(t) |
||
|
|
J |
C |
R |
L |
R |
0 |
R |
E,R |
6 |
uC(t) |
||
|
|
L |
R |
C |
0 |
R |
J |
R |
E,R |
7 |
uC(t) |
||
|
|
C |
L |
J |
R |
0 |
R |
E,R |
R |
8 |
iL(t) |
||
|
|
R |
C |
E,R |
L |
R |
0 |
J |
R |
9 |
iL(t) |
||
|
|
C |
0 |
R |
R |
L |
E,R |
R |
J |
10 |
uC(t) |
||
|
|
E,R |
R |
R |
C |
R |
0 |
L |
J |
11 |
iL(t) |
||
|
|
0 |
C |
R |
L |
E,R |
R |
J |
R |
12 |
uC(t) |
||
|
|
R |
E,R |
J |
R |
C |
R |
0 |
L |
13 |
iL(t) |
||
|
|
C |
R |
L |
E,R |
R |
-J |
R |
0 |
14 |
uC(t) |
||
|
|
J |
R |
L |
-E,R |
R |
R |
O |
C |
15 |
iL(t) |
||
|
|
C |
R |
L |
E,R |
R |
J |
R |
0 |
16 |
uC(t) |
||
|
|
L |
J |
0 |
R |
E,R |
R |
C |
R |
17 |
iL(t) |
||
|
|
L |
E,R |
C |
R |
J |
R |
R |
0 |
18 |
uC(t) |
||
|
|
R |
L |
0 |
-J |
R |
E,R |
R |
C |
19 |
iL(t) |
||
|
|
E,R |
R |
L |
J |
R |
0 |
R |
C |
20 |
uC(t) |
||
|
|
0 |
C |
R |
L |
J |
R |
E,R |
R |
21 |
iL(t) |
||
|
|
R |
J |
E,R |
R |
C |
R |
0 |
L |
22 |
uC(t) |
||
|
|
C |
R |
R |
0 |
L |
J |
R |
E,R |
23 |
iL(t) |
||
|
|
R |
C |
-J |
L |
R |
0 |
E,R |
R |
24 |
uC(t) |
||
|
|
C |
R |
E,R |
L |
0 |
L |
J |
R |
25 |
iL(t) |
||
|
|
0 |
E,R |
C |
R |
L |
R |
R |
J |
26 |
uC(t) |
||
|
|
E,R |
L |
R |
C |
R |
0 |
R |
J |
27 |
iL(t) |
||
|
|
C |
R |
L |
0 |
R |
-E,R |
J |
R |
28 |
uC(t) |
||
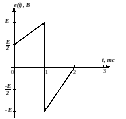
Вид источников показан в таблице 2
Таблица 2
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
31
|
32
|
33
|
34
|
35
|
36
|
