Задача № 2. Анализ переходных процессов в линейных цепях операторным методом
Д
ля
получения расчетной схемы, необходимо
в топологию цепи (рис. 1) поместить
элементы из табл. 1, которые указаны
буквами. Если в табл. 1 элементы записаны
через запятую, то они включаются в ветвь
последовательно. Направление источников
должно совпадать с направлением
указанным в ветвях топологической схемы
(рис. 1).
Вариант задается преподавателем или определяется по последним двум цифрам зачетной книжки (студенческого билета).
Назначение букв в таблице следующее: |
|
Численное значение элементов для всех вариантов равно: |
Е – постоянный источник ЭДС |
|
Е = 100 B |
J – постоянный источник тока |
|
J = 2A |
R - сопротивление |
|
R = 100 Ом |
L- индуктивность |
|
L = 0,1 Гн |
C - емкость |
|
C = 0,1 мкФ |
Клр - ключ на размыкание |
|
|
Клз - ключ на замыкание |
|
|
Для полученной расчетной схемы выполнить следующее.
Рассчитать переходной процесс для искомой величины операторным методом и построить график переходного процесса используя программу MathCad
выполнить моделирование схемы, применяя программу моделирования и анализа электротехнических схем Electronics Workbench или Multisim;
выполнить моделирование схемы в программе MatLab;
сравнить результаты расчета и моделирования.
Таблица 1
Вариант |
Номер ветви |
||||||||
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Найти |
|
|
E,R |
Клр |
R |
R |
L |
R |
C |
J |
il(t) |
|
|
J |
E,R |
Клр |
R |
R |
L |
R |
C |
uc(t) |
|
|
C |
J |
E,R |
Клр |
R |
R |
L |
R |
il(t) |
|
|
R |
C |
J |
E,R |
Клр |
R |
R |
L |
uc(t) |
|
|
L |
R |
C |
J |
E,R |
Клр |
R |
R |
il(t) |
|
|
R |
L |
R |
C |
J |
E,R |
Клр |
R |
ur3(t) |
|
|
R |
R |
L |
R |
C |
J |
E,R |
Клр |
i1(t) |
|
|
Клр |
R |
R |
L |
R |
C |
J |
E,R |
ul(t) |
|
|
E,R |
J |
R |
R |
L |
R |
C |
Клр |
ic(t) |
|
|
Клр |
E,R |
J |
R |
R |
L |
R |
C |
uc(t) |
|
|
C |
Клр |
E,R |
J |
R |
R |
L |
R |
ir8(t) |
|
|
R |
C |
Клр |
E,R |
J |
R |
R |
L |
ur6(t) |
|
|
L |
R |
C |
Клр |
E,R |
J |
R |
R |
i2(t) |
|
|
R |
L |
R |
C |
Клр |
E,R |
J |
R |
uc(t) |
|
|
R |
R |
L |
R |
C |
Клр |
E,R |
J |
i4(t) |
|
|
J |
R |
R |
L |
R |
C |
Клр |
E,R |
ul(t) |
|
|
J |
Клр |
R |
R |
L |
R |
C |
E,R |
il(t) |
|
|
E,R |
J |
Клр |
R |
R |
L |
R |
C |
uc(t) |
|
|
C |
E,R |
J |
Клр |
R |
R |
L |
R |
il(t) |
|
|
R |
C |
E,R |
J |
Клр |
R |
R |
L |
uc(t) |
|
|
L |
R |
C |
E,R |
J |
Клр |
R |
R |
ic(t) |
|
|
R |
L |
R |
C |
E,R |
J |
Клр |
R |
ul(t) |
|
|
R |
R |
L |
R |
C |
E,R |
J |
Клр |
il(t) |
|
|
Клр |
R |
R |
L |
R |
C |
E,R |
J |
uc(t) |
|
|
J |
E,R |
R |
R |
L |
R |
C |
Клр |
il(t) |
|
|
Клр |
J |
E,R |
R |
R |
L |
R |
C |
uc(t) |
|
|
C |
Клр |
J |
E,R |
R |
R |
L |
R |
il(t) |
|
|
R |
C |
Клр |
J |
E,R |
R |
R |
L |
uc(t) |
|
|
L |
R |
C |
Клр |
J |
E,R |
R |
R |
il(t) |
|
|
R |
L |
R |
C |
Клр |
J |
E,R |
R |
uc(t) |
|
|
R |
R |
L |
R |
C |
Клр |
J |
E,R |
il(t) |
|
|
E,R |
R |
R |
L |
R |
C |
Клр |
J |
uc(t) |
|
|
E,R |
Клр |
R |
R |
L |
R |
C |
J |
il(t) |
|
|
J |
E,R |
Клр |
R |
R |
L |
R |
C |
uc(t) |
|
|
C |
J |
E,R |
Клр |
R |
R |
L |
R |
il(t) |
|
|
R |
C |
J |
E,R |
Клр |
R |
R |
L |
uc(t) |
|
|
L |
R |
C |
J |
E,R |
Клр |
R |
R |
il(t) |
|
|
R |
L |
R |
C |
J |
E,R |
Клр |
R |
uc(t) |
|
|
R |
R |
L |
R |
C |
J |
E,R |
Клр |
il(t) |
|
|
Клр |
R |
R |
L |
R |
C |
J |
E,R |
uc(t) |
|
|
E,R |
J |
R |
R |
L |
R |
C |
Клр |
il(t) |
|
|
Клр |
E,R |
J |
R |
R |
L |
R |
C |
uc(t) |
|
|
C |
Клр |
E,R |
J |
R |
R |
L |
R |
il(t) |
|
|
R |
C |
Клр |
E,R |
J |
R |
R |
L |
uc(t) |
|
|
L |
R |
C |
Клр |
E,R |
J |
R |
R |
il(t) |
|
|
R |
L |
R |
C |
Клр |
E,R |
J |
R |
uc(t) |
|
|
R |
R |
L |
R |
C |
Клр |
E,R |
J |
il(t) |
|
|
J |
R |
R |
L |
R |
C |
Клр |
E,R |
uc(t) |
|
|
J |
Клр |
R |
R |
L |
R |
C |
E,R |
il(t) |
|
|
E,R |
J |
Клр |
R |
R |
L |
R |
C |
uc(t) |
|
|
C |
E,R |
J |
Клз |
R |
R |
L |
R |
il(t) |
|
|
R |
C |
E,R |
J |
Клз |
R |
R |
L |
uc(t) |
|
|
L |
R |
C |
E,R |
J |
Клз |
R |
R |
il(t) |
|
|
R |
L |
R |
C |
E,R |
J |
Клз |
R |
uc(t) |
|
|
R |
R |
L |
R |
C |
E,R |
J |
Клз |
il(t) |
|
|
Клз |
R |
R |
L |
R |
C |
E,R |
J |
uc(t) |
|
|
J |
E,R |
R |
R |
L |
R |
C |
Клз |
il(t) |
|
|
Клз |
J |
E,R |
R |
R |
L |
R |
C |
uc(t) |
|
|
C |
Клз |
J |
E,R |
R |
R |
L |
R |
il(t) |
|
|
R |
C |
Клз |
J |
E,R |
R |
R |
L |
uc(t) |
|
|
L |
R |
C |
Клз |
J |
E,R |
R |
R |
il(t) |
|
|
R |
L |
R |
C |
Клз |
J |
E,R |
R |
uc(t) |
|
|
R |
R |
L |
R |
C |
Клз |
J |
E,R |
il(t) |
|
|
E,R |
R |
R |
L |
R |
C |
Клз |
J |
uc(t) |
|
|
R |
Клз |
L |
R |
J |
C |
E,R0 |
R |
uc(t) |
|
|
R |
C |
R |
L |
Клз |
R |
J |
E,R |
il(t) |
|
|
E,R |
R |
R |
R |
C |
L |
Клз |
J |
uC(t) |
|
|
E,R |
L |
Клз |
R |
R |
R |
C |
J |
iL(t) |
|
|
J |
R |
E,R |
Клз |
L |
R |
R |
C |
uC(t) |
|
|
C |
R |
J |
E,R |
R |
Клз |
L |
R |
iL(t) |
|
|
R |
Клз |
C |
J |
R |
E,R |
R |
L |
uC(t) |
|
|
L |
E,R |
R |
C |
Клз |
J |
R |
R |
iL(t) |
|
|
R |
J |
L |
R |
E,R |
C |
Клз |
R |
uC(t) |
|
|
R |
C |
R |
L |
J |
R |
E,R |
Клз |
iL(t) |
|
|
Клз |
R |
R |
R |
C |
L |
J |
E,R |
uC(t) |
|
|
E,R |
L |
J |
R |
R |
R |
C |
Клз |
iL(t) |
|
|
Клз |
R |
E,R |
J |
L |
R |
R |
C |
uC(t) |
|
|
C |
R |
Клз |
E,R |
R |
J |
L |
R |
iL(t) |
|
|
R |
J |
C |
Клз |
R |
E,R |
R |
L |
uC(t) |
|
|
L |
E,R |
R |
C |
J |
Клз |
R |
R |
iL(t) |
|
|
R |
Клз |
L |
R |
E,R |
C |
J |
R |
uC(t) |
|
|
R |
C |
R |
L |
Клз |
R |
E,R |
J |
iL(t) |
|
|
J |
R |
R |
R |
C |
L |
Клз |
E,R |
uC(t) |
|
|
J |
L |
Клз |
R |
R |
R |
C |
E,R |
iL(t) |
|
|
E,R |
R |
J |
Клз |
L |
R |
R |
C |
uC(t) |
|
|
C |
R |
E,R |
J |
R |
Клз |
L |
R |
iL(t) |
|
|
R |
Клз |
C |
E,R |
R |
J |
R |
L |
uC(t) |
|
|
L |
J |
R |
C |
Клз |
E,R |
R |
R |
iL(t) |
|
|
R |
E,R |
L |
R |
J |
C |
Клз |
R |
uC(t) |
|
|
R |
C |
R |
L |
E,R |
R |
J |
Клз |
iL(t) |
|
|
Клз |
R |
R |
R |
C |
L |
E,R |
J |
uC(t) |
|
|
J |
L |
E,R |
R |
R |
R |
C |
Клз |
iL(t) |
|
|
Клз |
R |
J |
E,R |
L |
R |
R |
C |
uC(t) |
|
|
C |
R |
Клз |
J |
R |
E,R |
L |
R |
iL(t) |
|
|
R |
E,R |
C |
Клз |
R |
J |
R |
L |
uC(t) |
|
|
L |
J |
R |
C |
E,R |
Клз |
R |
R |
iL(t) |
|
|
R |
Клз |
L |
R |
J |
C |
E,R |
R |
uC(t) |
|
|
R |
C |
R |
L |
Клз |
R |
J |
E,R |
iL(t) |
|
|
E,R |
R |
R |
R |
C |
L |
Клз |
J |
uC(t) |
|
|
L |
J |
R |
C |
E,R |
R |
Клз |
R |
iL(t) |
П
ример
расчета переходного процесса в цепи
второго порядка операторным методом
Для полученной расчетной схемы (рис. 8)рассчитать переходной процесс для тока в шестой ветви i6(t) операторным методам и построить график переходного процесса, еслиЕ=100 В, J=2 А, R=100 Ом, L=0.1 Гн, C=0,1 мкФ.
Решение
О
пределяем
независимые начальные условия (ННУ),
т.е. величины, подчиняющиеся законам
коммутации - uС(0-)
и iL(0-).
ННУ определяются
в схеме до коммутации для момента времени
t=0-.Для
определения величины uС(0-)
и
iL(0-)необходимо
воспользоваться схемой замещения цепи
на постоянном токе, в которой емкость
заменяется обрывом, индуктивность
заменяется проводником и ключ замкнут
(рис. 9). Запишем уравнения по законам
Кирхгофа
(1)
Решим полученные уравнения в программе MathCad (рис. 10)
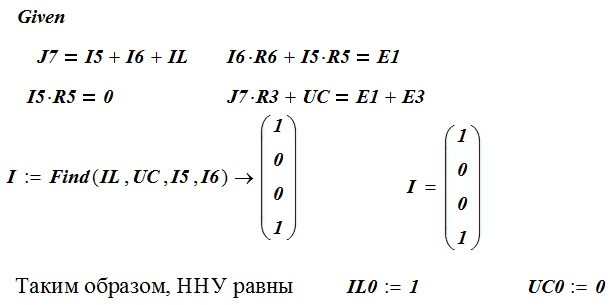
Таким образом, ННУ равны uС(0-) = UC =0 В; iL(0-) = 1 A.
Ненулевое начальное напряжение на емкости учитываем источником ЭДС EС(р), а ток в индуктивности - EL(р) (рис .10). Для цепи после коммутационной конфигурации составляем эквивалентную операторную схему замещения (рис. 11).
В операторной схеме замещения параметры схемы имеют следующие значения:
; 
;
;
где
по закону коммутации
и
.
П
олученная
операторная схема замещения (рис. 11)
является сложной схемой, поэтому для
нахождения операторного изображения
тока в шестой ветви I6(p)
Для указанных контуров в схеме рис. 11
запишем систему уравнений: по законам
Кирхгофа.
(2)
Решим полученные уравнения в программе MathCad (рис. 12)
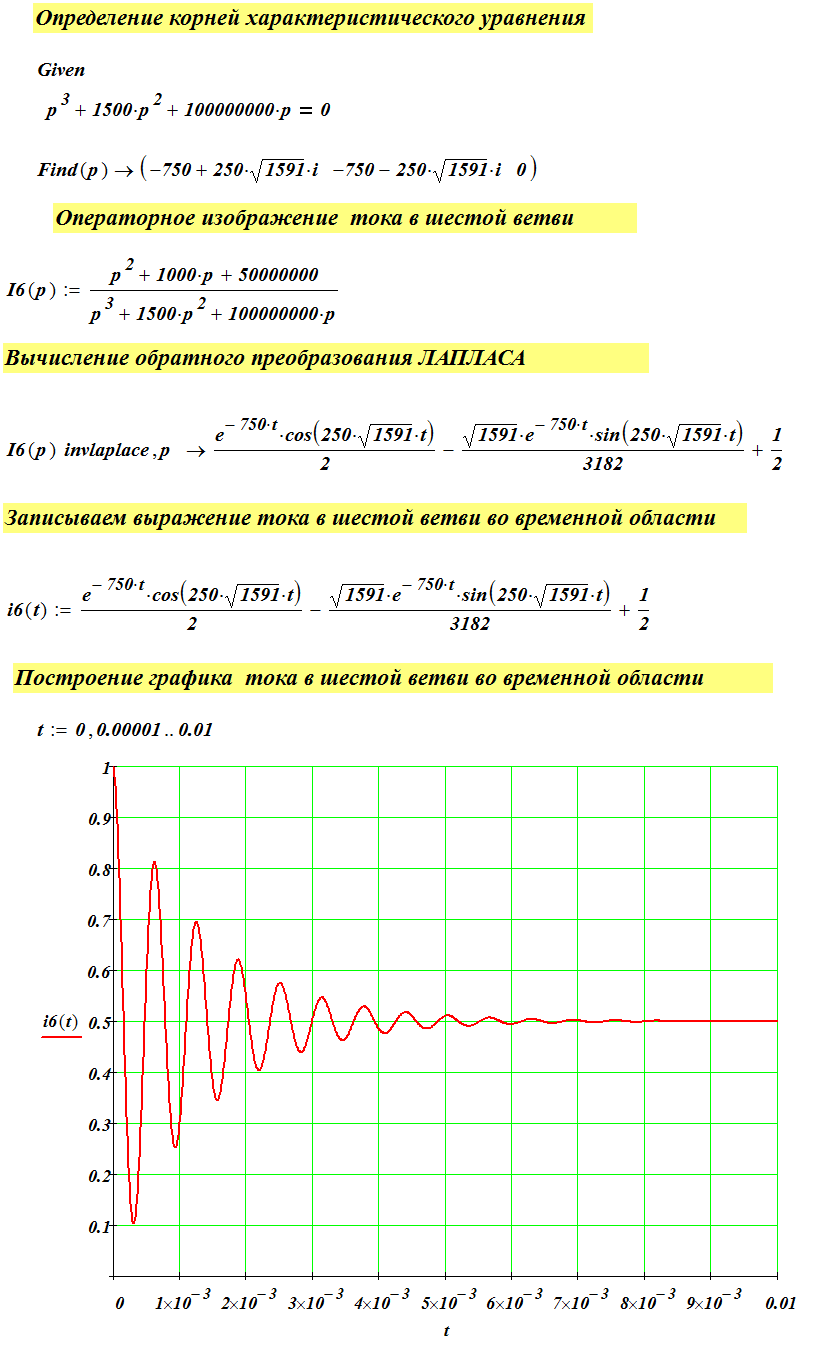
Применяя программу моделирования и анализа электротехнических схем ELECTRONICS WORKBENCH, необходимо:
включить в собранную схему в ELECTRONICS WORKBENCH (рис. 17) постоянные источники как для операторного метода и снять осциллограмму для искомой величины (тока или напряжения) (рис.18 и рис.19) и сравнить с результатами расчета, выполненными операторным методом (рис. 20).
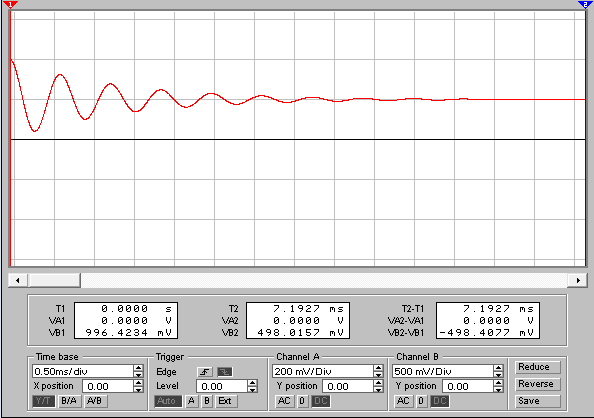
Рис. 17
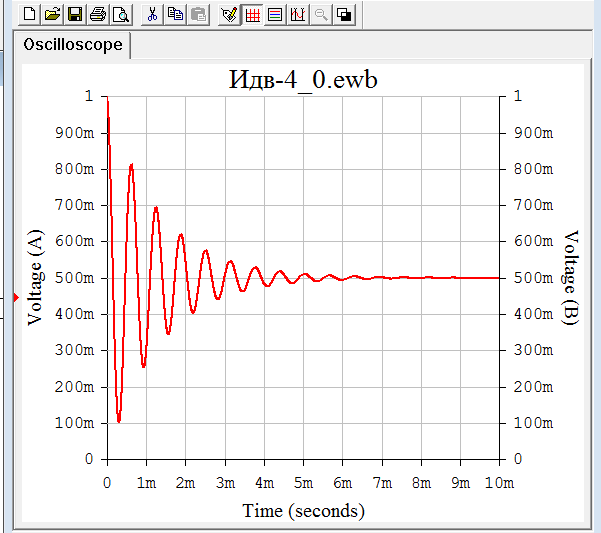
Рис. 18