Прядок расчета переходного процесса классическим методом:

Для схемы после коммутации записывается система интегро-дифференциальных уравнений по законам Кирхгофа:

;

.

Из полученной системы выводится дифференциальное уравнение относительно искомой величины:

где x(t) – это ток или напряжение в элементе или ветви;

F(t) – это источники электрической энергии, в цепи после коммутации.

n-порядок дифференцирования уравнения.

В электротехнике n будет определять порядок цепи после коммутации, который определяется количеством емкостей и индуктивностей:

n= ,

где -количество емкостей после коммутации;

-количество индуктивностей после коммутации;

-количество узлов, образованных ветвями с индуктивностями или ветвями с индуктивностями и источниками тока;

-количество контуров, образованных ветвями с емкостями или ветвями с емкостями и источниками ЭДС.

Примечание: из этого пункта при анализе переходных процессов в электротехнике определяется только порядок цепи в схеме после коммутации.

Записывается решение дифференциального.уравнения в общем виде:

где x(t)= -напряжение или ток в каком-то элементе или ветви;

-принужденная составляющая, определяется в цепи после коммутации;

-свободная составляющая;

- постоянные интегрирования;

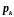- корни характеристического уравнения.

Определение принужденной составляющей в схеме после коммутации, когда - это величина определяется методами расчета простых и сложных цепей.

Составление характеристического уравнения для схемы после коммутации и нахождение корней этого уравнения. Характеристические уравнения составляются из условия, когда . Для этого необходимо все источники положить равными нулю, т.е. источник ЭДС заметь проводником, а ветвь с источником тока удалить.

В полученной схеме без источников, разрываем любую ветвь и определяем комплексное входное сопротивление относительно разрыва, используя метод эквивалентных преобразований или уравнения Кирхгофа, затем необходимо сделать замену переменных и записать характеристическое уравнение и найти корни этого уравнения .

Составляются уравнения для определения постоянных интегрирования А₁,А₂...А_n.

Чтобы получить систему относительно А₁,А₂...А_n необходимо уравнение продифференцировать n-1 раз.

В результате получаем систему:

Для решения полученной системы необходимо положить t=0₊

(*)

Таким образом, чтобы найти А₁,А₂ …А_nиз системы со звездочкой, необходимо знать начальные условия (НУ).

6.Определение начальных условий.

Начальные условия делятся на два вида:

1 независимые начальные условия (ННУ);

2 зависимые начальные условия (ЗНУ).

6.1 Определение ННУ. Они определяются в схеме до коммутации, когда =0_-. К ННУ относятся величины, подчиняющиеся законам коммутации: .Для определения этих величин используется метод цепей на постоянном или переменном токе.

6.2определение ЗНУ. Они определяются в схеме после коммутации для момента времени =0₊. К ЗНУ относятся все величины, не подчиняющиеся законам коммутации: и любые производные и т. д.

ЗНУ определяются из системы интегро-дифференциальных уравнений, записанных из уравнений Кирхгофа для мгновенных значений, затем эта система дифференцируется (n-2) раза и полученные системы записываются для значения t=0₊. Из этих систем находят ЗНУ, которые будут являться функциями ННУ и источников.

По найденным начальным условиям пункта 6 определяем постоянные интегрирования А₁,А₂ …А_nрешая систему со звездочкой пункта 5. Найденное значение коэффициентов А₁,А₂ …А_nподставляем в общее решение пункта 2, записываем ответ и строим график переходного процесса.