Метод переменных состояний.
Этот метод позволяет автоматизировать формирование дифференциальных уравнений 1-ог порядка, удовлетворяющих условиям, а полученные уравнения решаются численными методами Эйлера, Рунге-Кутта. В качестве переменных состояния желательно выбирать величины, подчиняющиеся законам коммутации. Т.к. для решения системы дифференциальных уравнений надо знать ННУ. Если выбираем другие величины, то необходимо знать не только независимые НУ, но и зависимые НУ.
где А и В - числа , которые зависят от конфигурации цепи и являются функциями элементов R,L,C.
Здесь
и
-
столбцовые матрицы соответственно
переменных состояния и их первых
производных по времени;
-
матрица-столбец источников внешних
воздействий;
-
столбцовая матрица выходных (искомых)
величин;
-
квадратная размерностью
n x n (где n – число
переменных состояния) матрица параметров,
называемая матрицей Якоби;
-
прямоугольная матрица связи между
источниками и переменными состояния
(количество строк равно n, а столбцов –
числу источников m);
-
прямоугольная матрица связи переменных
состояния с искомыми величинами
(количество строк равно числу искомых
величин к, а столбцов – n);
-
прямоугольная размерностью к
x m матрица связи
входа с выходом.
Начальные условия для уравнения (2) задаются вектором начальных значений (0).
Формирование уравнений методом переменных состояний.
При ручном способе формирования уравнений 1и2 удобно использовать метод наложения.
Алгоритм.
Для после коммутационной цепи необходимо перейти к схеме замещения, в которой емкость и индуктивность заменяются источниками.
В полученной схеме замещения, используя метод наложения, получаем выражение:
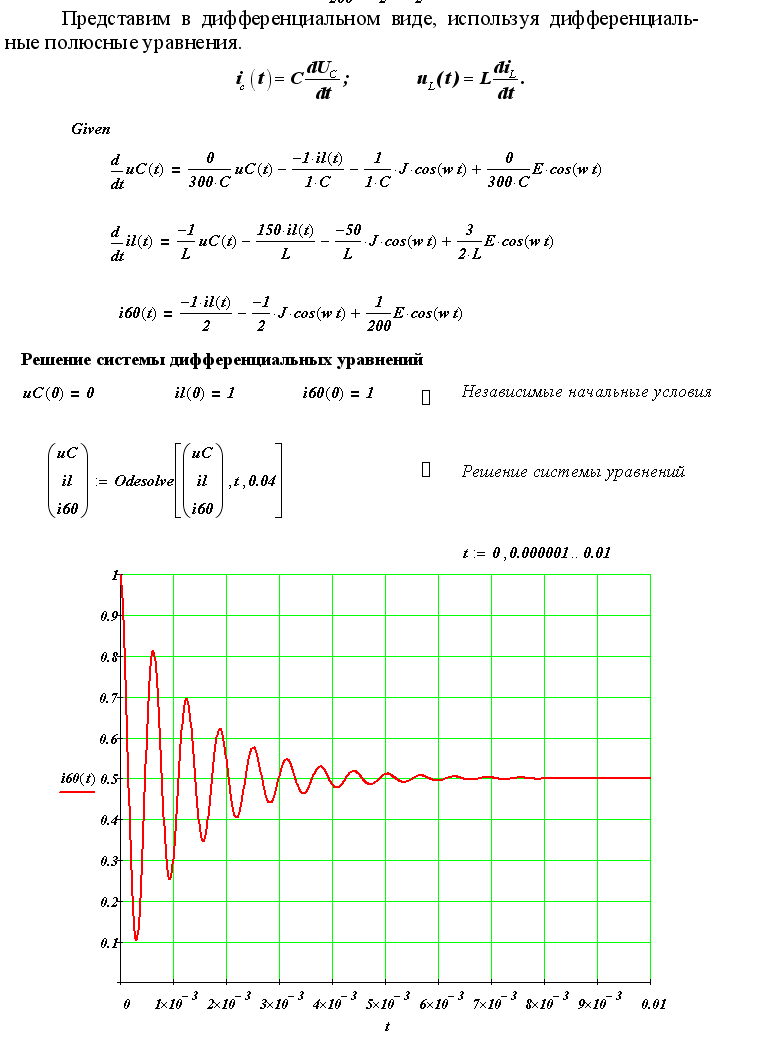
Их можно представить в дифференциальном виде, используя дифференциальные полюсные уравнения.
Если необходимо определить закон изменения тока и напряжения тех величин, которые не подчиняются законам коммутации, нужно составить алгебраическое уравнение по методу наложения.
3
.Полученные
системы дифференциальных и алгебраических
уравнений заменяем на основании
рекуррентных функций Эйлера, Рунге-Кутта
и решаем на ЭВМ
Метод пространства состояний
При расчете цепи методом пространства состояний режим ее работы описывается матричными уравнениями:
,
(1)
,
(2)
причем, уравнение (1) - дифференциальное, а уравнение (2) - алгебраическое. В этих уравнениях:
X = [ хi (t) ] - матрица-столбец переменных состояния, i изменяется в пределах [1; n ];
X = [ хi (t) ] - матрица-столбец производных ( скоростей изменения ) переменных состояния;
Y = [yj (t)] - матрица-столбец выходных реакций или вектор выхода, j изменяется в пределах [ 1; l];
V = [vк(t)]-матрица-столбец внешних воздействий или вектор входа, k изменяется в пределах [ 1; m ];
n - порядок электрической цепи;
m - количество задающих источников;
l - количество искомых выходных реакций;
A, B, C, D - матрицы связей для исследуемой цепи.
Матрицы связей A, B, C, D определяются с помощью уравнений Кирхгофа или с помощью канонической процедуры построения матриц связей. Каноническая процедура не требует предварительного составления уравнений Кирхгофа, так как элементы матриц A,B,C,D являются псевдопередаточными коэффициентами вспомогательных резистивных цепей.
Покажем алгоритм получения матриц A, B, C, D на примере цепи II порядка, содержащей источник напряжения и источник тока, для которой уравнения состояния в развернутом виде запишутся:
(3)
В этой системе i1, i2 - искомые выходные токи (реакции). В общем случае это могут быть любые токи и напряжения в любых ветвях.
Объединим полученные уравнения в матричное уравнение, содержащее расширенную матрицу реакций и переменных состояния:
(4)
Так
как данное матричное уравнение является
верным для любого момента времени t
0+ , т.е. значения коэффициентов
матриц A, B, C, D являются величинами
постоянными, то правомерной является
следующая зависимость:
(5)
Для определения искомых коэффициентов применим метод наложения (принцип суперпозиции). Если в уравнении (5) попеременно полагать все начальные значения iL (0+), uC (0+), Е1 (0+), J2 (0+) равными нулю, кроме одного, приравниваемого единице, то значения элементов расширенной матрицы iL (0+), uC (0+), i1 (0+), i2 (0+) совпадут с элементами соответствующего столбца матриц А, В, С, D.
Принимая во внимание, что
и
,
Пример расчета переходного процесса в цепи второго порядка операторным методом
Для полученной расчетной схемы (рис. 8)рассчитать переходной процесс для тока в шестой ветви i6(t) операторным методам и построить график переходного процесса, если
Е=100 В, J=2 А, R=100 Ом, L=0.1 Гн, C=0,1 мкФ.
Решение
Определяем независимые начальные условия (ННУ), т.е. величины, подчиняющиеся законам коммутации - uС(0-) и iL(0-). ННУ определяются в схеме до коммутации для момента времени t=0-.Для определения величины uС(0-) и iL(0-)необходимо воспользоваться схемой замещения цепи на постоянном токе, в которой емкость заменяется обрывом, индуктивность заменяется проводником и ключ замкнут (рис. 9). Запишем уравнения по законам Кирхгофа
(1)
Решим полученные уравнения в программе MathCad (рис. 10)
Таким образом, ННУ равныuС(0-) = UC =0 В; iL(0-) = 1 A.
Для после коммутационной цепи необходимо перейти к схеме замещения, в которой емкость и индуктивность заменяются источниками
Запишем уравнения по законам Кирхгофа
Решим полученные уравнения в программе MathCad
