6.Асимптоты графика

Построение графика функции значительно упрощается, если знать его асимптоты.

Прямая х=а является вертикальной асимптотой графика функции y=f(x), если .

Вертикальные асимптоты обычно сопутствуют точкам разрыва 2-го рода или их следует искать на концах ее области определения.

Прямая y=kx+b является наклонной асимптотой графика функции y=f(x), если существуют конечные пределы . Если хотя бы один из пределов не существует или равен бесконечности, то вертикальной асимптоты не существует. В частности, если k=0, то . Поэтому y=b – уравнение горизонтальной асимптоты.

Замечание: Асимптоты графика y=f(x) при х→ + и х→- могут быть разными. Поэтому при нахождении пределов следует отдельно рассматривать случай, когда х→ + и х→-.

7.Наибольшее и наименьшее значение функции

Пусть функция y=f(x) непрерывна на отрезке [a;b]. Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке отрезка [a;b], либо на его концах.

Получаем следующее правило нахождения наибольшего и наименьшего значений функции на [a;b]:

1. Найти критические точки функции на интервале (a;b).

2. Вычислить значения функции в найденных критических точках.

3. Вычислить значения функции на концах отрезка.

4. Среди всех вычисленных значений выбрать наибольшее и наименьшее.

Пример: Найти наибольшее и наименьшее значение функции на отрезке

[1;6].

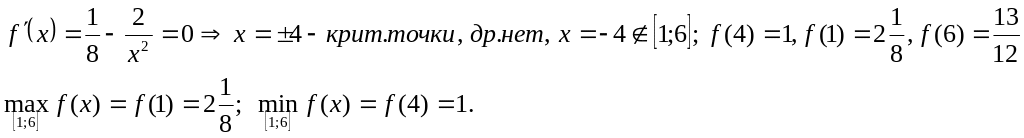
Замечание 1: Если функция y=f(x) на отрезке [a;b] имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.

Пример: На прямой y=2x найти такую точку, чтобы сумма квадратов расстояний от

нее до точек А(2;0) и в(0;4) была наименьшей.

Замечание 2: Если функция не имеет критич. точек на отрезке, то на нем функция возрастает или убывает и свое наиб. (наим.) значение принимает на концах отрезка.

Пример: Чему равно наибольше значение функции f(x)=sin(sinx)?

1) наибольшее значение;

2) f(z)=sin z возрастает при Этот отрезок включает отрезок [-1;1]. Значит,

.

8.Задачи с экономическим содержанием

Пусть Q- количество реализованной продукции, R(Q)- функция дохода, C(Q)- функция затрат на производство продукции. В реальности вид этих функций зависит в первую очередь от способа производства, организации инфраструктуры и т.п. Прибыль от реализации произведенной продукции находим по формуле:

H(Q)=R(Q)-C(Q).

В микроэкономике известно утверждение: для того чтобы прибыль была максимальной, необходимо, чтобы предельный доход и предельные издержки были равны. Т.к. предельные показатели равны производной функции, то этот принцип можно записать в виде R  (Q)=C (Q). Действительно, из необходимого условия экстремума для функции H(Q) следует, что H  (Q)=0, откуда и получается приведенный ранее основной принцип.

Пример: Пусть доход от реализации товара R=PQ,, где Q – количество единиц произведенного товара; P- его цена, причем P зависит от Q: P=P(Q)=1000-0,2Q. Затраты на производство товара составляют C=200+2Q. Определите, при каком объёме выпуска продукции Q прибыль H=R-C будет максимальной.

Подставим выражения для R и C в формулу прибыли:

. Найдем критические точки:

Убедимся, что в этой точке прибыль будет максимальной: при Q<2495 производная H >0, при Q>2495 производная H <0. Следовательно, при переходе через точку Q=2495 производная меняет свой знак с «+» на «- », т.е. функция Н достигает в этой точке своего максимума.

Т.о., максимальная прибыль будет получена при объёме выпуска продукции в 2495 единиц.

Пример: Производитель реализует свою продукцию по цене p за единицу, а издержки при этом задаются зависимостью . Найти оптимальный для производителя объём выпуска продукции и соответствующую ему прибыль.

Обозначим объём выпускаемой продукции х.Составим функцию прибыли , где px – доход от реализуемой продукции.

1. Находим .

2. Находим критические точки: =0, откуда не рассматриваем по смыслу задачи.

3. Находим и определяем знак 2-ой производной при : ( )<0 ( в данном случае при любом х>0), следовательно, при прибыль С(х) максимальна.

4. Находим максимум функции (т.е. максимальный размер прибыли)

Пример: Капитал в 1 млрд.рублей может быть размещен в банке под 50% годовых или инвестирован в производство, причем эффективность вложения ожидается в размере 100%, а издержки задаются квадратичной зависимостью. Прибыль облагается налогом в p%. При каких значениях p вложение в производство является более эффективным, нежели чистое размещение капитала в банке?

Пусть х (млрд.руб.) инвестируется в производство, а 1-х – размещается под проценты. Тогда размещенный капитал через год станет равным , а капитал, вложенный в производство: . Издержки составят , т.е. прибыль от вложения в производство . Налоги составят т.е. чистая прибыль окажется равной

Общая сумма через год составит: , и тебуется нати максимальное значение этой функции на отрезке [0;1].

Имеем , т.е. согласно 2-му достаточному условию экстремума - точка максимума.

Чтобы принадлежало отрезку [0;1], необходимо выполнение условия .

Т.о., если p>25, то выгоднее ничего не вкладывать в производство и разместить весь капитал в банк. Если p<25, то можно показать, что при х=

,

Т.е. вложение в производство является более выгодным, чем чистое размещение под проценты.

8