35.Скалярное произведение двух векторов и его свойства. Ортогональность векторов.

 Определение скалярного произведения

Скалярным произведением двух ненулевых векторов а и b называетсячисло, равное произведению длин этих векторов на косинус угла междуними.

Обозначается ab,а* b(или( а, b)).Итак, по определению,

  

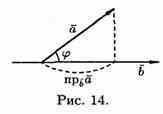
Формуле   (6.1)   можно   придать   иной   вид.   Так   как |a| cosg=пр _ba, (см. рис.14), a |b| cosg = пр _ab, то получаем:

      

 т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

Скалярное произведение векторов обладает следующими четырьмя свойствами:

1. ab = ba (переместительное свойство);

2. (αa)b = α(ba) (сочетательное свойство относительно числового мно-

жителя );

3. (a + b)c = ac + bc (распределительное свойство относительно суммы

векторов);

4. aa > 0, если a - ненулевой вектор, и aa = 0, если a - нулевой вектор.

Ортогона́льность— понятие, являющееся обобщением перпендикулярности для линейных пространств с введённым скалярным произведением.

Если скалярное произведение двух элементов пространства равно нулю, то они называются ортогональными друг другу.Важной особенностью понятия является его привязка к конкретному используемому скалярному произведению: при смене произведения ортогональные элементы могут стать неортогональными, и наоборот.

36.Прямоугольная декартова система координат

Среди декартовых систем координат простейшей является прямоугольная декартова система координат. Определение 1. Декартова система координат {0;   ;   } на плоскости называется прямоугольной, если   и   - ортогональные единичные векторы. Аналогично определяется прямоугольная декартова система координат {0;   ;   ;   } в пространстве; в этом случае векторы   ,   ,   также являются взаимно перпендикулярными и единичными. Базисные векторы   ,   прямоугольной декартовой системы координат на плоскости обозначают обычно  ,  , базисные векторы   ,   ,   прямоугольной декартовой системы координат обозначают  ,  ,  . Соответственно разложение радиус-вектора   по базису записывают в виде  (для плоскости);  (для пространства). В первом случае точка М имеет координаты х, у, во втором случае - координаты х, у, z. Определение 2. Проекцией вектора   на единичный вектор   называется число  , где   = ( ,  ) - угол между векторами   и    . Координаты х, у, z вектора  , полученные как коэффициенты линейной комбинации базисных векторов, в прямоугольном базисе совпадают с проекцией вектора   на базисные орты  ,  ,   соответственно, а длина вектора   равна  . Определение 3. Числа pic.cosa.jpg[/img],  , cosy.jpg[/img] называются направляющими косинусами вектора  . Направляющие косинусы вектора совпадают с координатами (проекциями) его орта   и между собой связаны соотношением  . Отметим, что базис  ,  ,   называют ортонормированным, так как  .

37. Угол между векторами. Неравенство Коши-Буняковского.

Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы.

Угол между векторами — угол между направлениями этих векторов (наименьший угол).

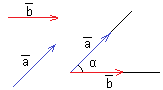
По определению, угол между двумя векторами находится в промежутке [0°; 180°]. Угол между векторами   обозначается так:  . Если векторы перпендикулярны, то угол между ними равен 90º. Если векторы сонаправлены, в частности один из них или оба нулевые, то угол между ними равен 0^о. Если противоположно направленные векторы, то угол между ними равен 180º. Угол между двумя ненулевыми векторами находится с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними (скалярное произведение для двух векторов с координатами (x₁; y₁) и (x₂; y₂) вычисляется по формуле: x₁x₂ + y₁y₂).