
- •31. Линейные операции над векторами и их свойства.
- •32. Линейно зависимые и не зависимые векторы.
- •33. Базис векторов. Координаты вектора в базисе.
- •34. Условия коллениарности двух векторов.
- •35.Скалярное произведение двух векторов и его свойства. Ортогональность векторов.
- •36.Прямоугольная декартова система координат
- •37. Угол между векторами. Неравенство Коши-Буняковского.
- •38. Векторное произведение двух векторов и его свойства.
- •39. Смешанные произведения трех векторов и его свойства. Объем пирамиды.
- •40. Радиус-вектор точки . Координаты вектора.
31. Линейные операции над векторами и их свойства.
Операция сложения двух векторов - правило треугольника.
Покажем как происходит сложение двух векторов.
Сложение
векторов ![]() и
и ![]() происходит
так: от произвольной точки A откладывается
вектор
происходит
так: от произвольной точки A откладывается
вектор ![]() ,
равный
,
далее от точки B откладывается
вектор
,
равный
,
далее от точки B откладывается
вектор ![]() ,
равный
,
и вектор
,
равный
,
и вектор ![]() представляет
собой сумму
векторов
и
.
Такой способ сложения двух векторов
назвается правилом
треугольника.
представляет
собой сумму
векторов
и
.
Такой способ сложения двух векторов
назвается правилом
треугольника.
Проиллюстрируем сложение не коллинеарных векторов на плоскости по правилу треугольника.
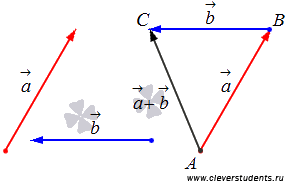
А на чертеже ниже показано сложение сонаправленных и противоположно направленных векторов.
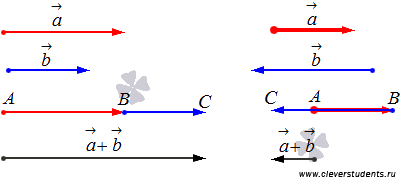
Операция умножения вектора на число.
Сейчас разберемся как происходит умножение вектора на число.
Умножение
вектора на число k соответствует
растяжению вектора в k раз
при k > 1 или
сжатию в ![]() раз
при 0 < k < 1,
при k = 1 вектор
остается прежним (для отрицательных k еще
изменяется направление на противоположное).
Если произвольный вектор умножить на
ноль, то получим нулевой вектор.
Произведение нулевого вектора и
произвольного числа есть нулевой вектор.
раз
при 0 < k < 1,
при k = 1 вектор
остается прежним (для отрицательных k еще
изменяется направление на противоположное).
Если произвольный вектор умножить на
ноль, то получим нулевой вектор.
Произведение нулевого вектора и
произвольного числа есть нулевой вектор.
К примеру, при умножении вектора на число 2 нам следует вдвое увеличить его длину и сохранить направление, а при умножении вектора на минус одну треть следует уменьшить его длину втрое и изменить направление на противоположное. Приведем для наглядности иллюстрацию этого случая.

Свойства операций над векторами.
Итак,
мы определили операцию сложения векторов
и операцию умножения вектора на число.
При этом для любых векторов ![]() и
произвольных действительных чисел
и
произвольных действительных чисел ![]() можно
при помощи геометрических построений
обосновать следующие свойства
операций над векторами.
Некоторые из них очевидны.
можно
при помощи геометрических построений
обосновать следующие свойства
операций над векторами.
Некоторые из них очевидны.
Свойство коммутативности
 .
.
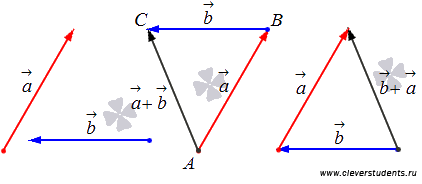
Свойство ассоциативности сложения
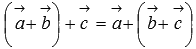 .
.
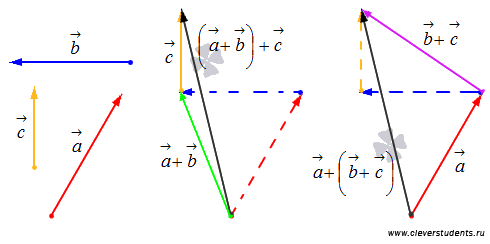
Существует нейтральный элемент по сложению, которым является нулевой вектор
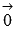 ,
и
,
и 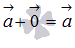 .
Это свойство очевидно.
.
Это свойство очевидно.Для любого ненулевого вектора существует противоположный вектор
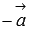 и
верно равенство
и
верно равенство 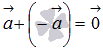 .
Это свойство очевидно без иллюстрации.
.
Это свойство очевидно без иллюстрации.Сочетательное свойство умножения
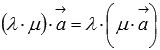 .
К примеру, растяжение вектора в 6 раз
можно произвести, если сначала его
растянуть вдвое и полученный вектор
растянуть еще втрое. Аналогичного
результата можно добиться, например,
сжав вектор вдвое, а полученный вектор
растянуть в 12 раз.
.
К примеру, растяжение вектора в 6 раз
можно произвести, если сначала его
растянуть вдвое и полученный вектор
растянуть еще втрое. Аналогичного
результата можно добиться, например,
сжав вектор вдвое, а полученный вектор
растянуть в 12 раз.Первое распределительное свойство
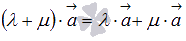 .
Это свойство достаточно очевидно.
.
Это свойство достаточно очевидно.Второе распределительное свойство
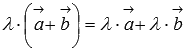 .
Это свойство справедливо в силу подобия
треугольников, изображенных ниже.
.
Это свойство справедливо в силу подобия
треугольников, изображенных ниже.

Нейтральным числом по умножению является единица, то есть,
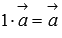 .
При умножении вектора на единицу с ним
не производится никаких геометрических
преобразований.
.
При умножении вектора на единицу с ним
не производится никаких геометрических
преобразований.
32. Линейно зависимые и не зависимые векторы.
В линейной алгебре линейная зависимость — это свойство, которое может иметь подмножество линейного пространства. Для этого должна существовать нетривиальная линейная комбинация элементов этого множества, равная нулевому элементу. Если такой комбинации нет, то есть коэффициенты единственной такой линейной комбинации равны нулю, множество называется линейно независимым.
Свойства
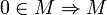 линейно
зависимо
линейно
зависимо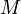 линейно
независимо
линейно
независимо 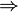
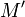 линейно
независимо для всех
линейно
независимо для всех 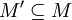
линейно зависимо линейно зависимо для всех

Значение
Линейные системы уравнений
Линейная система уравнений, где — количество переменных, имеет однозначное решение тогда и только тогда, когда столбцы её основной матрицы являются линейно независимыми.
Ранг матриц
Ранг матрицы равен числу её линейно независимых строк или столбцов.
Геометрический смысл
Векторы и линейно зависимы тогда и только тогда, когда они коллинеарны (лежат на параллельных прямых).
Векторы линейно зависимы тогда и только тогда, когда они компланарны (лежат в одной плоскости).
Базис
Базис линейного пространства является в частности множеством линейно независимых векторов.
