
- •1.Вопрос
- •§1. Понятие ''качество продукции''. Система показателей качества
- •2.Ворос.
- •3Вопрос.
- •4. Вопрос
- •5Вопрос.
- •6.Вопрос.
- •7.Вопрос объектов свойств надежности
- •8.Вопрос
- •9.Вопрос
- •1.6.1 Классификация событий
- •10.Вопрос Отказ
- •11.Вопрос
- •12.Вопрос
- •13.Вопрос Основные показатели безотказности для ремонтируемых объектов
- •14.Вопрос Основные показатели долговечности
- •15.Вопрос
- •16.Вопрос Основные показатели сохраняемости
- •17.Вопрос Комплексные показатели надежности
- •18.Вопрос
- •19.Вопрос
- •20.Вопрос. Основные законы распределения случайных величин
20.Вопрос. Основные законы распределения случайных величин
Нормальный закон распределения и его значение в теории вероятностей. Логарифмически нормальный закон. Гамма-распределение. Экспоненциальный закон и его использование в теории надёжности, теории очередей. Равномерный закон. Распределения хи-квадрат, Вейбула, Стьюдента, Фишера.
Нормальный закон распределения (закон Гаусса)
Плотность
вероятности нормально распределённой
случайной величины ![]() выражается
формулой
выражается
формулой
![]() (8.1)
(8.1)
Эта формула показывает, что нормальный закон распределения полностью определяется математическим ожидание и дисперсией случайной величины. Таким образом, математическое ожидание и дисперсия полностью характеризуют нормально распределённую случайную величину.
Логарифмически нормальное распределение
Говорят,
что случайная величина ![]() имеет
логарифмически нормальное распределение
(сокращённо логнормальное
распределение),
если её логарифм
имеет
логарифмически нормальное распределение
(сокращённо логнормальное
распределение),
если её логарифм ![]() распределён
нормально, то есть если
распределён
нормально, то есть если
![]()
Гамма-распределение
Говорят,
что случайная величина
имеет
гамма-распределение с параметрами ![]() и
и ![]() ,
если её плотность распределения
вероятностей имеет вид
,
если её плотность распределения
вероятностей имеет вид
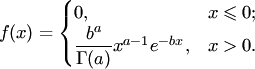 где
где 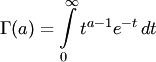 —
гамма-функция Эйлера.
—
гамма-функция Эйлера.
Экспоненциальный закон распределения
Экспоненциальным
распределением называется частный
случай гамма-распределения с параметрами ![]() ,
то есть то есть плотность вероятности
в этом случае
,
то есть то есть плотность вероятности
в этом случае
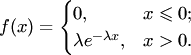
Распределение Вейбула
Случайная
величина
подчиняется
закону распределения Вейбула с
параметрами ![]() ,
если её плотность распределения
вероятностей записывается в виде
,
если её плотность распределения
вероятностей записывается в виде
Математическое ожидание и мода случайной величины, распределённые по закону Вейбула, имеют следующий вид:
![]()
Равномерный закон распределения
Случайная
величина
называется
распределённой равномерно на отрезке ![]() ,
если её плотность распределения
вероятностей постоянна на данном
отрезке:
,
если её плотность распределения
вероятностей постоянна на данном
отрезке:
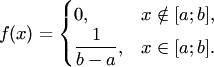
Распределение
хи-квадрат ![]()
Частный
случай гамма-распределения с
параметрами ![]() и
и ![]() называется
распределением хи-квадрат с
называется
распределением хи-квадрат с ![]() степенями
свободы (пишут
степенями
свободы (пишут ![]() ).
Если случайная величина
подчиняется
закону
,
то её плотность распределения вероятностей
есть
).
Если случайная величина
подчиняется
закону
,
то её плотность распределения вероятностей
есть
Распределение Стьюдента
Распределение
хи-квадрат Случайная величина ![]() есть
отношение двух независимых случайных
величин
есть
отношение двух независимых случайных
величин ![]() и
и ![]() ,
то есть
,
то есть
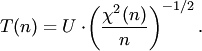
Распределение Фишера
Пусть
случайная величина ![]() равна
отношению двух независимых случайных
величин
равна
отношению двух независимых случайных
величин ![]() и
и ![]() ,
то есть
,
то есть
![]()
