35. Приведите примеры известных вам законов распределения св (не менее трех).

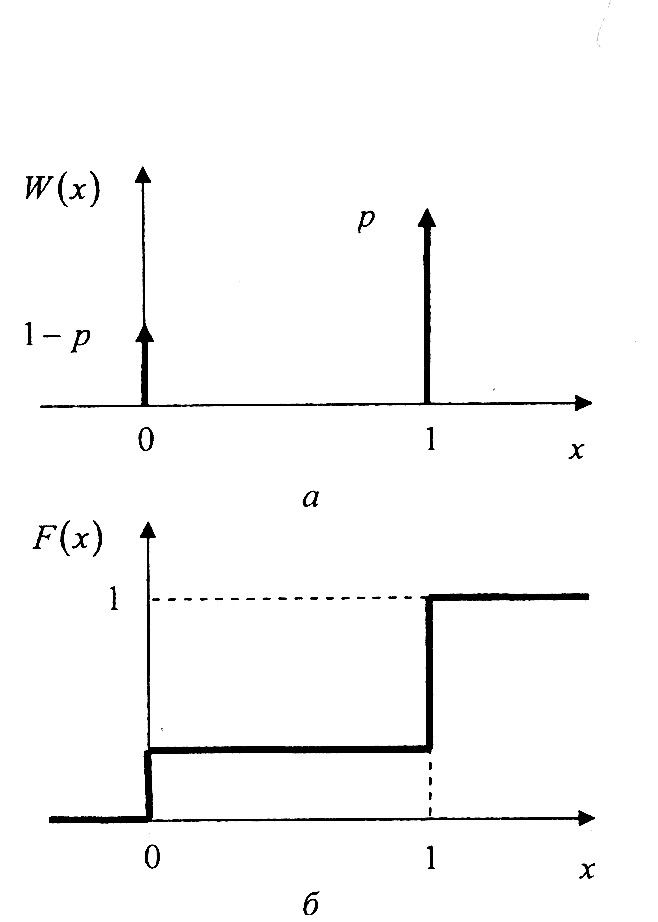
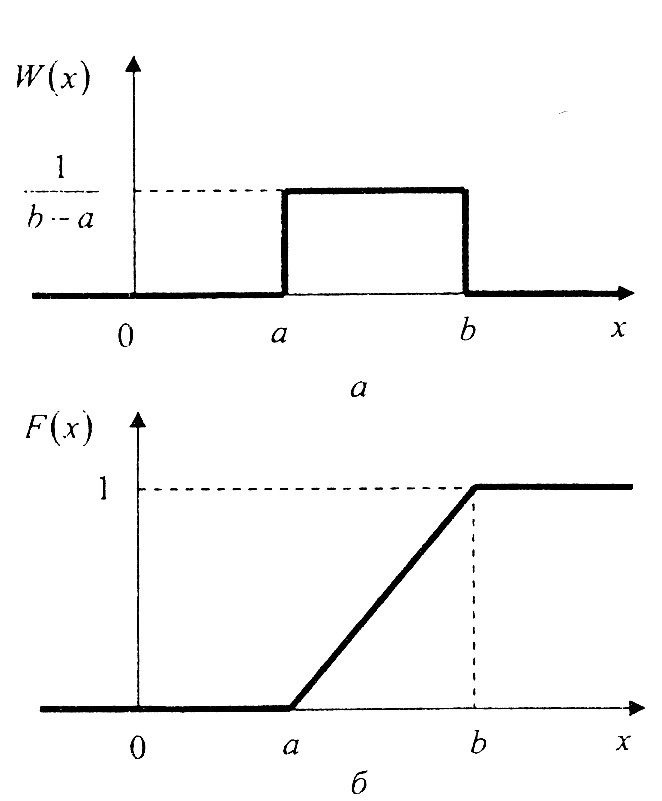
1) Распределение Бернулли: 2)Равномерное распределение

F(x)=0, x≤0; F(x)=1-p, 0<x≤1; F(x)=1, x>1 F(x)=0, x≤a; F(x)= , a<x≤b; F(x)=1, x>b

W(x)=1-p, x=0; W(x)=p, x=1 W(x)=A, a≤x≤b; W(x)=0, x<a и x>b

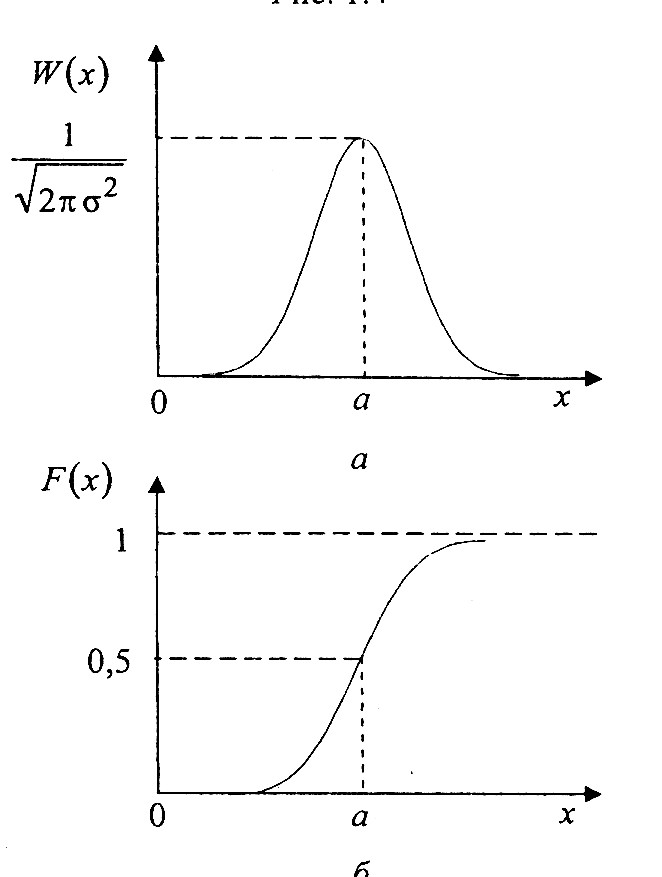
3) Нормальное распределение

,

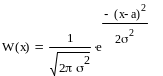
36. СВ равновероятно принимает значения +1 или -2. Найти ее математическое ожидание и дисперсию.

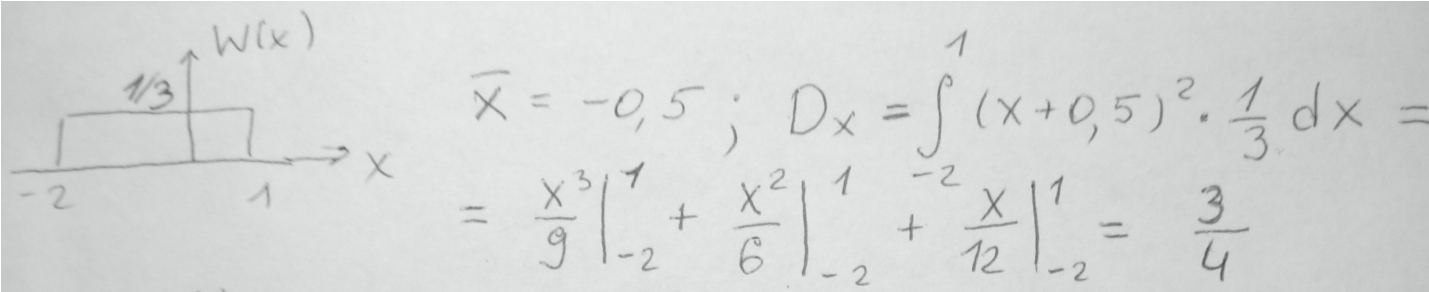
37. Св имеет равномерную пв в интервале [-1; 3]. Найти ее математическое ожидание, медиану, квартили и дисперсию.

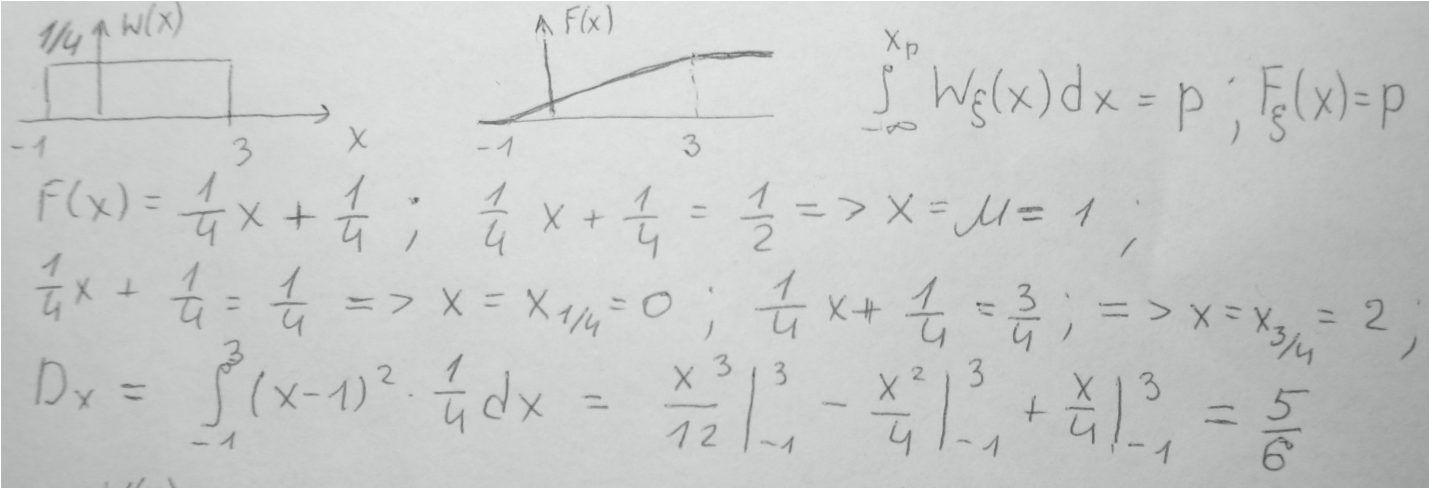
38.СВ принимает значения +1 или -1. Вероятность значения +1 равна 0,4. Записать и построить ПВ и ФР этой СВ.

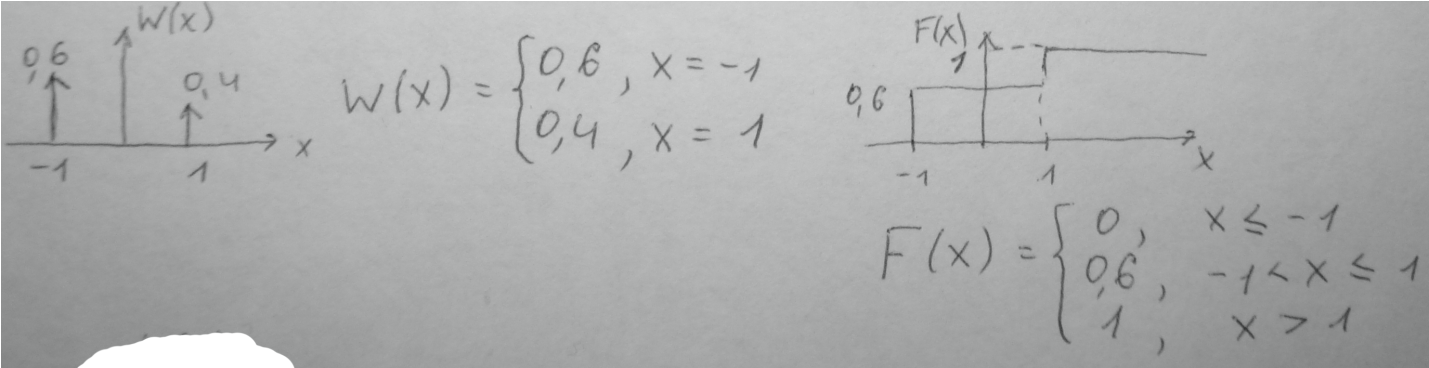
39. СВ Х имеет равномерную ПВ в интервале [-1; 3]. Построить ПВ и ФР для СВ Y = 2X-1.

40. СВ Х имеет нормальную ПВ с математическим ожиданием 2 и дисперсией 4. Записать ПВ и ФР случайной величины Y = 3X+8.

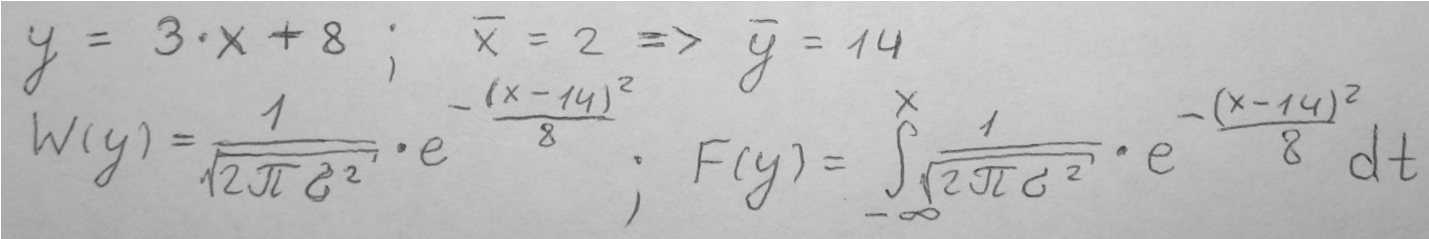
41. Дать определение случайной функции, случайного процесса. Какие характеристики дают полное вероятностное описание СП? Запишите математические выражения для этих характеристик.

Случайным процессом (t) называется функция двух аргументов (t, ), где   ,  – множество элементарных событий; t  T, T – область определения функций (t, ). При фиксированном значении t (t, ) является случайной величиной, а для каждого фиксированного  (заданного элементарного события) (t, ) зависит только от t и определяет реализацию СП (траекторию, выборочную функцию).

П олное вероятностное описание СП. Говорят, что имеется полное статистическое описание СП (t), если для любых п и t₁, t₂, …, t_n  T можно задать функцию распределения

.

При этом должны быть выполнены условие симметрии, состоящее в том, что

,

г де i₁, i₂, …, i_n – перестановка чисел 1, 2, …, п; и условие согласованности:

.

Столь же полное вероятностное описание дадут многомерная ПВ:

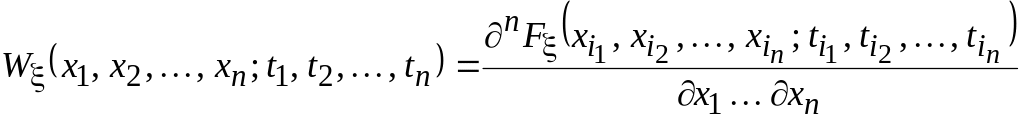
и многомерная ХФ:

,

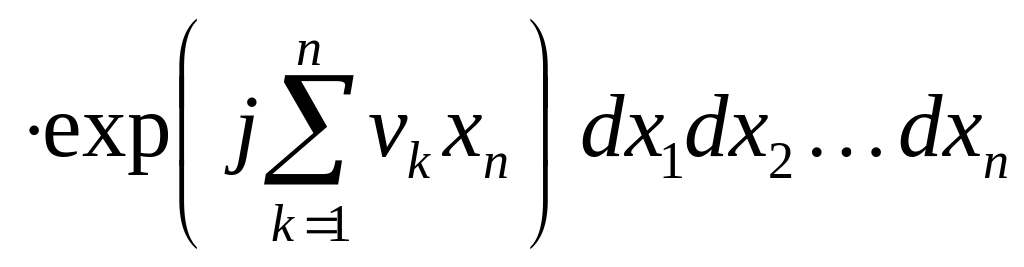
или кумулянтная функция:

.

Как и для многомерных случайных величин, для описания случайных процессов могут быть использованы моменты. Начальные и центральные моменты определяются, соответственно, выражениями:

,

.

Приведенные выражения зависят от моментов времени t₁, t₂, …, t_n и поэтому называются моментными функциями. Наиболее часто для описания СП используют математическое ожидание (среднее значение) случайного процесса (t) , где t  T и корреляционную функцию (КФ):

,

г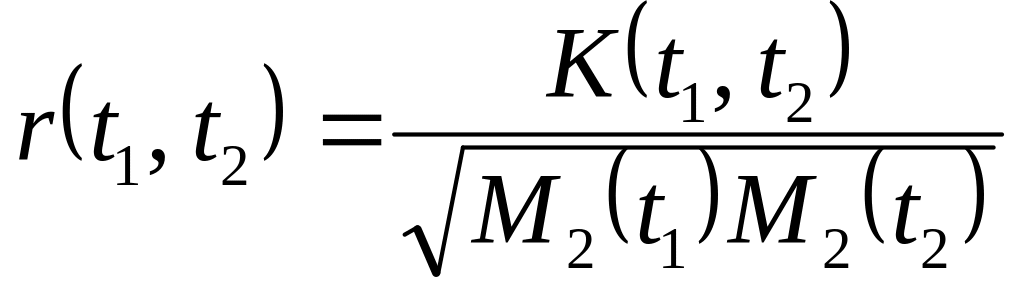 де t₁, t₂  T . Таким образом, корреляционная функция определяет зависимость ковариации случайных величин ₁ = (t₁) и ₂ = (t₂) от моментов времени t₁ и t₂, в которых берутся отсчеты СП (t). Как и для случайных величин, можно ввести коэффициент корреляции

,

где М₂(t₁) и М₂(t₂) – дисперсии отсчетов процесса в моменты времени t₁ и t₂. Напомним, что .

Преобразование Фурье реализаций СП , если оно существует, является случайной функцией переменной f и, как и сама реализация x(t), не может быть использована для описания СП.