26. Чему равно математическое ожидание суммы св? Ответ аргументировать.
Математическое ожидание суммы любых
(зависимых и независимых) СВ равно сумме
математических ожиданий, т.к.
=
=
+
.
Выполняя внутреннее интегрирование в
первом слагаемом по
,
а во втором по
,
получим
=
+
=
.
27. Чему
равно математическое ожидание произведения
независимых СВ? Ответ
аргументировать. Математическое
ожидание произведения независимых СВ
равно произведению их математических
ожиданий, т.е.
=
=
=
,
т.к. переменные в последнем двойном
интеграле разделяются.
28. Чему равно математическое ожидание линейной комбинации попарно независимых св? Ответ аргументировать.
Математическое ожидание линейной
комбинации СВ
равно линейной комбинации с теми же
коэффициентами
математических ожиданий
,
т.е.
=
.
Таким образом, для оператора математического
ожидания (статистического усреднения)
справедлив принцип суперпозиции, т.е.
это – линейный оператор (функционал).
29. Как определяются дисперсии суммы и разности двух независимых св? Ответ аргументировать.
Дисперсия суммы или разности независимых
СВ равна сумме их дисперсий. Для суммы
или разности независимых СВ
и
дисперсия равна
=
=
.
Возводя в квадрат и используя введенные
обозначения, будем иметь
=
+
±2
=
+
,
где
- равные нулю первые центральные моменты
СВ
и
30. Чему
равна дисперсия линейной комбинации
попарно независимых СВ? Ответ
аргументировать.Дисперсия линейной
комбинации
попарно независимых СВ
равна
.
D (X1+X2+…+Xn) =D(X1)+D(X2)+…+D(Xn).
31. Как определяются смешанные центральные моменты распределения для совокупности дискретных и непрерывных св? Что такое ковариация случайных величин X и y? Что она показывает?
-для
непрерывных СВ
2) Пусть 
— две случайные величины, определённые
на одном и том же вероятностном
пространстве. Тогда их ковариация
определяется следующим образом:
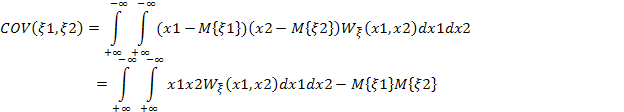
3) Она характеризует меру линейной связи
между СВ 
.
32. Что такое коэффициент корреляции? Какие значения он может принимать?
Что означает r = –1; 0; 1? Какие случайные величины называются ортогональными?
Коэф. корреляции – безразмерное
отношение: rξ1ξm
=
К нему переходят, чтобы исключить
зависимость ковариации от величины
разброса СВ ξl и ξm
относительно средних значений, при ее
нормировке относительно их
среднеквадратических значений
и
.
2) |rξ1ξm|≤1.
r=0, то СВ назыв.
Некоррелированными или ортогональными;
|r|=1 означает линейную
связь между СВ ξ1 и ξm
. 3) Ортогональными или некоррелированными
являются случайные величины, ковариация
которых равна нулю.
33. Доказать, что независимые св некоррелированы.
Если СВ ξi и ξm незавиимы то они некоррелированы (ортоганальны) так как:
=
Обратное утверждение в общем случае несправедливо.
34. Всегда ли независимые случайные величины являются некоррелированными? Всегда ли некоррелированные случайные величины являются независимыми?
Из независимости следует некоррелированность.
Обратное утверждение не верно.
