1. Что такое случайная величина? Какие случайные величины называются дискретными, а какие – непрерывными? Что такое СВ смешанного типа (дискретно-непрерывная)? Какой вид имеют в общем случае ПВ и ФР этих случайных величин?

С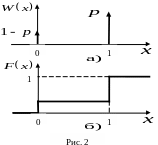 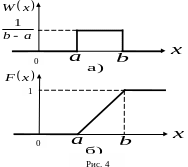В является обобщением понятия случайного события, при котором каждому элементарному событию ставится в соответствие некоторое число _. Пусть рассматриваемая величина принимает значения из множества X, которое может быть конечно X = , счетно X = СВ, для которой X – конечное или счетное множество, называется дискретной. Случайная величина называется непрерывной (относится к классу, типу непрерывных СВ), если существует неотрицательная функция , удовлетворяющая при любых равенству

= , а .

2. Что такое функция распределения св? Как она связана с плотностью вероятности св? Какие свойства функции распределения вам известны?

ФР - вероятность события, состоящего в том, что СВ будет меньше значения , являющегося аргументом функции распределения, т.е. .

свойства ФР:1) – неотрицательная неубывающая функция.2) Функция непрерывна слева, - =0. 3).Функция распределения позволяет определить вероятность попадания СВ в интервал как = .4). Функция терпит разрыв первого рода при тех значениях , которые принимаются СВ с конечной вероятностью . Величина скачка в точке разрыва равна вероятности . Функция распределения может иметь не более чем счетное множество скачков.5). В частности, =0 и =1. Связь св и пв смотри в 1 вопросе.

3. Что такое плотность вероятности СВ? Как связаны между собой функция распределения и плотность вероятности случайной величины? Какие свойства плотности вероятности вам известны?

Свойства ПВ:1. 2. При любых X справедливо равенство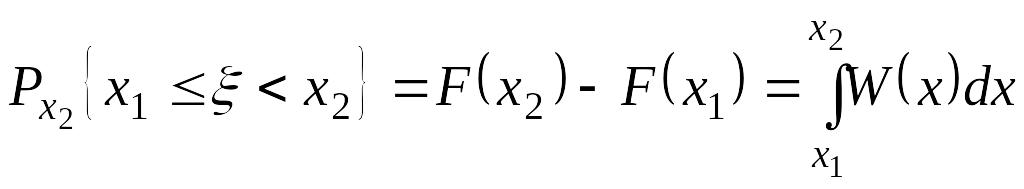 .Если непрерывна в точке , то с точностью до бесконечно малых высших порядков

.3. Следствием свойства 2 является условие нормировки Связь ПВ иСВ: = , а .

4. Что такое характеристическая функция СВ? Как она связана с плотностью вероятности? Может ли ХФ некоторой СВ иметь форму прямоугольника?

Преобразование Фурье ПВ определяет характеристическую функцию (ХФ) СВ = . обратно

5. Перечислите основные свойства характеристической функции. Может ли она быть чисто мнимой функцией?

1) =1. 2) ХФ непрерывна для всех , для нее выполняются следующие условия: ; и , где - знак комплексного сопряжения.

6. Как определяются начальные моменты распределения дискретных и непрерывных СВ? Какие начальные моменты чаще всего используются на практике? Что они характеризуют?

Под начальными моментами СВ понимают величины , среди которых особую роль играет , называемый математическим ожиданием или средним значением СВ . Для дискретных СВ, задаваемых распределением ( ), =1,2,…, , математическое ожидание равно , если записанный ряд сходится абсолютно. Математическое ожидание является точкой концентрации значений СВ в том смысле, что среднеквадратический разброс значений СВ относительно минимален.

7. Как определяются центральные моменты распределения дискретных и непрерывных СВ? Какие центральные моменты чаще всего используются на практике? Что они характеризуют?

Центральные моменты = . Важнейшим центральным моментом является , называемый дисперсией СВ и обозначаемый обычно как . Дисперсия – рассеяние СВ относительно математического ожидания . . На практике используют , - чтобы оценить насколько плоская вершина (для норм.распределения равно 0)

8. Какова размерность плотности вероятности, функции распределения, математического ожидания, дисперсии, среднеквадратического отклонения, k-го начального момента распределения, k-го центрального момента распределения случайной величины?

Размерность ПВ обратна размерности СВ; ФР- безразмерна; мат.ожидание- в единицах СВ; дисперсия- квадрат едениц измерения СВ; СКО- еденицы измер.СВ

9. Доказать, что первый центральный момент распределения СВ всегда равен нулю. -

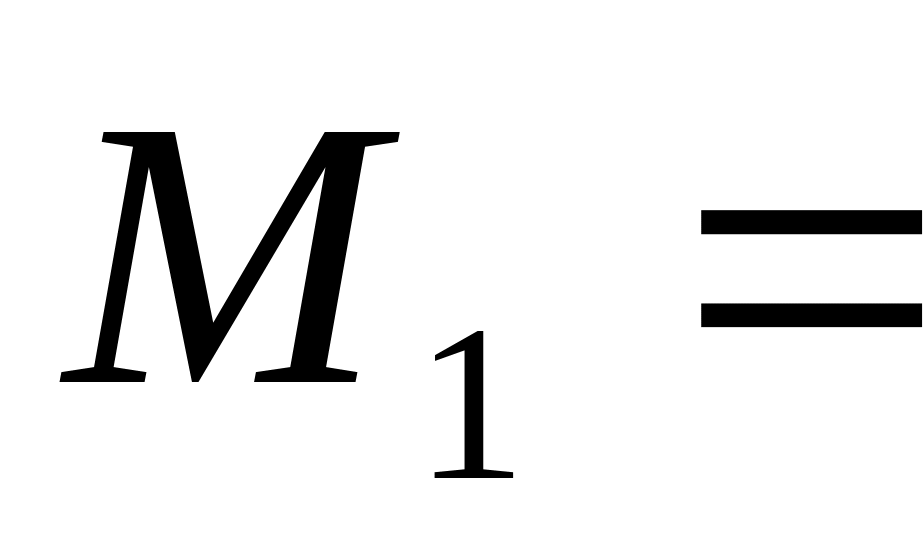
10. Доказать утверждение: .

.

11. Доказать утверждение:

для функции СВ

= = и = =

.

=

=

Следовательно

12.К случайной величине добавили детерминированную константу А. Как изменились плотность вероятности; функция распределения; характеристическая функция; среднее; дисперсия; среднеквадратичное отклонение?

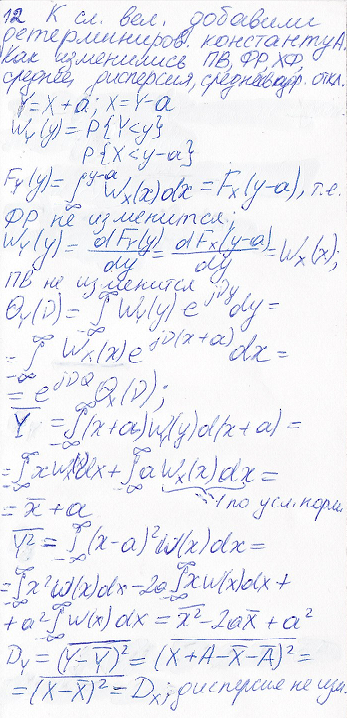
13.Случайную величину умножили на детерминированную константу А. Как изменились плотность вероятности; функция распределения; распределения; характеристическая функция; среднее; дисперсия; среднеквадратичное отклонение?

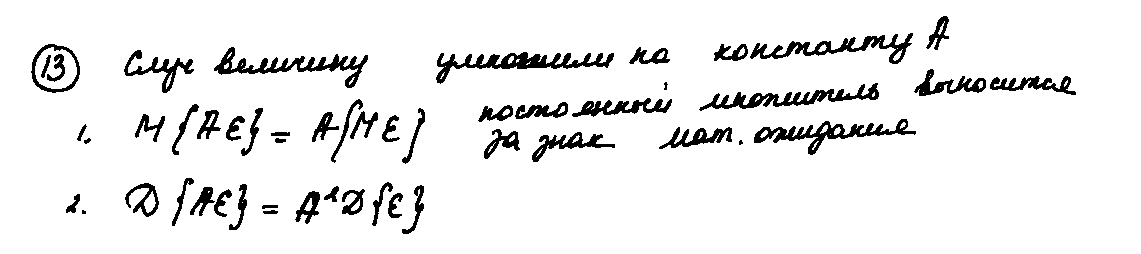
14.Как, зная ФР некоторой случайной величины, определить вероятность попадания этой СВ в заданный интервал? Как, зная ПВ некоторой случайной величины, определить вероятность попадания этой СВ в заданный интервал х? Конкретизируйте ответ, если х  0.

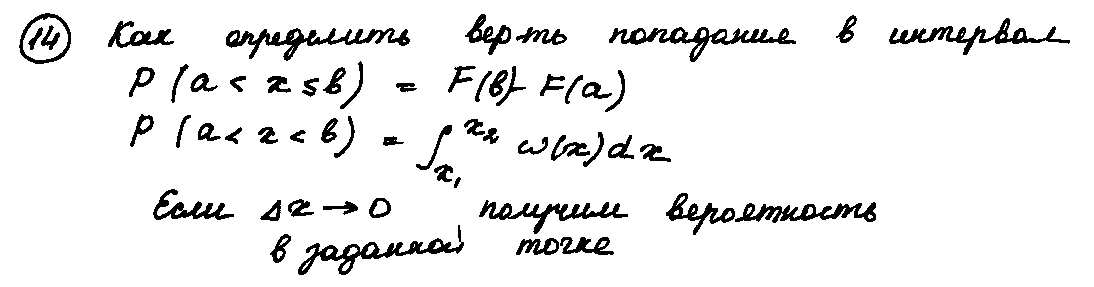
15.Может ли случайная величина иметь второй начальный момент, равный 9 при математическом ожидании 3,1?

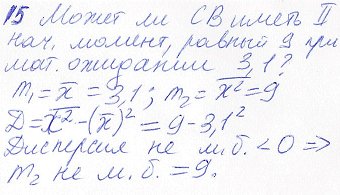
16.Что такое р-квантиль? Как найти р-квантиль через ФР и ПВ? Что такое медиана? При каком условии медиана и математическое ожидание совпадают?

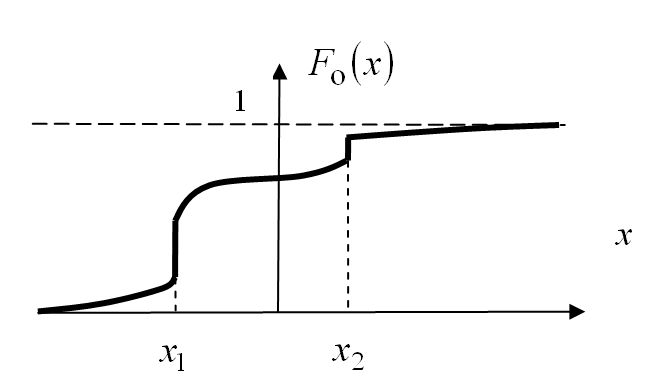
17. Что называется модой распределения случайной величины? Какие распределения называются унимодальными, какие  полимодальными? Привести примеры.

Мода – абсцисса локального максимума ПВ. По числу мод распределения делятся на унимодальные и полимодальные. Унимодальное распределение - это распределение, имеющее только одну моду. Полимодальное распределение – это распределение имеющее несколько мод.

Н а рис. Полимодальное распределение. Унимодальное тоже самое, только с одним пиком.

18. Как определить плотность вероятности случайной величины Y, связанной со случайной величиной X соотношением Y = f(X), если плотность вероятности величины X известна, и существует обратная функция X = (Y)? Как выглядит результат, если обратная функция многозначна, например, ?

Wн(Y)=Wст. (x(y))*|dx(y)/dy| При Y=X² Wн(Y)=Wст. (x(y))*(1/2 sqrt(y))