18. Определение скорости и ускорения точки при координатном способе задания движения

Связь векторного способа задания движения и координатного дается соотношением

Из определения скорости

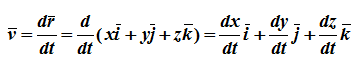
Проекции скорости на оси координат равны производным соответствующих координат по времени:

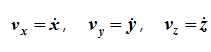
Модуль и направление скорости определяются выражениями

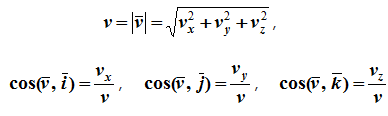
Из определения ускорения

Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени

Модуль и направление ускорения определяются выражениями

19. Фывфывфывфвфывфыв

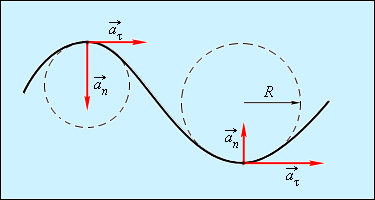
Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю: 

Вектор   направлен по касательной к траектории.

Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению.

Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).

Рисунок 1.1.6. Движение по дугам окружностей

Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент: 

Вектор   всегда направлен к центру окружности (см. §1.6).

Из рис. 1.1.5 видно, что модуль полного ускорения равен 

Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение  , скорость   и ускорение  . Путь l является скалярной величиной. Перемещение  , скорость   и ускорение   – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.

Модель. Вектор и его проекции на координатные оси

Модель. Сложение и вычитание векторов

20. Угловая скорость и угловое ускорение

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:    Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ (рис. 2). Размерность угловой скорости dim ω = Т^-1, а ее единица — радиан в секунду (рад/с).  Линейная скорость точки (см. рис. 1)   

Рис.1

т.е

v=ωR

В векторном виде формулу для линейной скорости можно написать как векторное произведение:    При этом модуль векторного произведения, по определению, равен ωRsin(ω, R), а направление совпадает с направлением поступательного движения правого винта его вращения от ω к R. 

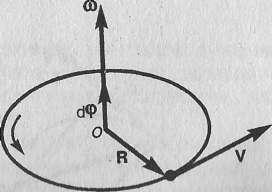
Рис.2

Если ω=const, то вращение равномерное и его можно характеризовать периодом вращения Т - временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2π. Так как промежутку времени Δt=Т соответствует Δφ=2π, то ω=2π/T, откуда 

Т = 2π/ω.

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения: 

n= 1/T = ω/(2π),

откуда 

ω = 2πn.

Угловым ускорением называется векторная величина, равная первой производной yгловой скорости по времени:   

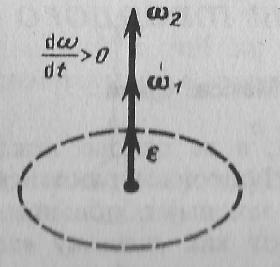
Рис.3

При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω (рис. 3), при замедленном - противонаправлен ему (рис. 4). 

Рис.4

Тангенциальная составляющая ускорения a_τ=dv/dt , v = ωR и    Нормальная составляющая ускорения    Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение а_τ, нормальное ускорение а_n) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами: 

s = Rφ, v = Rω, а_τ = R?, a_n = ω²R.

В случае равнопеременного движения точки по окружности (ω=const) 

ω = ω₀ ± ?t, φ = ω₀t ± ?t²/2,

где ω₀ — начальная угловая скорость.