1.Аксиомы статики

   Статикой называется раздел теоретической механики в котором излагается общее учение о силах и изучается равновесие материальных тел, находящихся под действием сил.

    Под равновесием понимают состояние покоя тела по отношению к инерциальной системе отсчета, связанной обычно с неподвижным телом.

    В качестве модели реального материального тела, в статике рассматривается абсолютно твердое тело - тело расстояние между любыми двумя точками которого всегда остается постоянным.

    Совокупность сил, действующих на твердое тело, называется системой сил.

    В основе статики лежат аксиомы - экспериментально установленные законы, справедливость которых проверена практической деятельностью человека.

    Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находится в равновесии только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны:

F₁ = - F₂.

     Система сил F₁ и F₂ называется уравновешивающейся, или эквивалентной нулю: F₁+ F₂ = 0.

(Здесь и далее векторные величины выделены жирным шрифтом).

    Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если к ней добавить или от нее отнять уравновешенную систему сил.

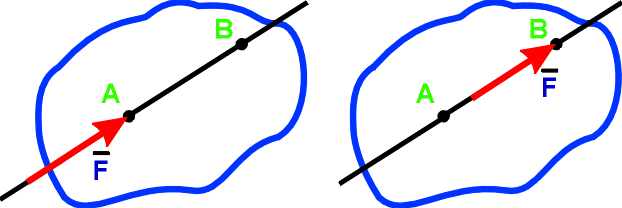
   Следствие. Не нарушая состояния твердого тела, силу можно переносить по линии ее действия в любую точку тела, т. е. сила - вектор скользящий.

 

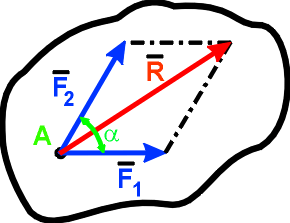
     Аксиома 3. Две силы, приложенные к телу в одной точке, можно заменить одной, приложенной в той же точке, которая является диагональю параллелограмма, построенного на этих силах как на сторонах:

R = F₁+ F₂ .

    Сила R, которая эквивалентна данной системе сил F₁и F₂ называется равнодействующей. Ее модуль вычисляется по формуле

R = [F12+ F22 + 2F1F2cos]1/2

где - угол между силами F₁ и F₂ .

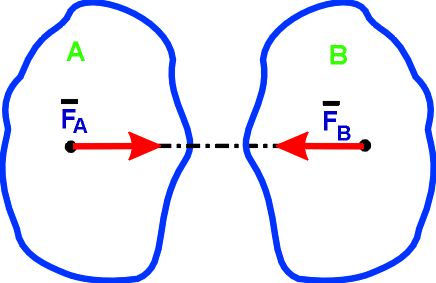
    Аксиома 4. Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены по одной прямой в противоположные стороны:

F_A = - F_B.

   Cилы F_A и F_B не образуют уравновешенную систему сил, так как они приложены к разным телам.

    Аксиома 5. Равновесие деформируемого тела не нарушится, если тело считать отвердевшим (абсолютно твердым).

    Следует помнить, что условия равновесия, являющиеся необходимыми и достаточными для твердого тела, являются необходимыми, но не достаточными для соответствующегодеформируемого тела.

    Две основные задачи статики.

    1. Задача о приведении системы сил: заключается в замене данной стстемы сил другой, наиболее простой, ей эквивалентной.

    2. Задача о равновесии состоит в определении условий, при которых система сил приложенная к телу будетуравновешенной системой.

2.Закон параллелограмма сил.закон равенства действия противодействию.

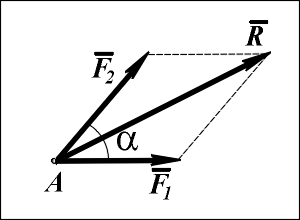
Закон параллелограмма сил: две силы F₁ и F₂, приложенные к телу в одной точке, имеют равнодействующую силу R, приложенную в той же точке и являющуюся диагональю параллелограмма, построенного на этих силах, как на сторонах.

Вектор R называют геометрической суммой векторов F₁ и F₂ : R =F₁+F₂.  Модуль равнодействующей может быть вычислен с использованием теоремы косинусов по следующей формуле:

R=(F₁²+F₂²+2F₁F₂cos  )  ;

где   - угол между силами F₁ и F₂.

Принцип отвердения: равновесие деформируемого твердого тела, находящегося под действием данной системы сил, не нарушится, если тело считать абсолютно твердым.

2. закон деиствияпротиводеиствию- ньютон