15.1 Сурет. Arma(1,1) процессі үшін таңдамалы acf коррелограммасы.

процессінің автокорреляциялық функциясы q мерзім лагынан кейін «үзіледі», ал дербес автокорреляциялық функция p мерзім лагынан кейін «үзіледі».

Тәжірибеде нақты уақыттық қатар үшін таңдамалы ACF және PACF жосығы сәйкес процессінің теоретикалық ACF және PACF мінез-құлқына «ұқсас» болу керек.

15.2. Интеграцияланған процесс

Көптеген стационарлық емес уақыттық қатарлар стационарлыққа айырмасын табу жолымен, түрлендіріле алады. Егер - стационарлық емес уақыттық қатар, ал - стационарлық уақыттық қатар болса, онда бірінші ретті интеграцияланған уақыттық қатар болып табылады.

Әрі қарай, егер стационарлық емес, ал стационарлық уақыттық қатар болса, онда екінші ретті интеграцияланған уақыттық қатар деп аталады.

Жалпы жағдайда, егер стационарлық емес уақыттық қатар үшін 1, 2, ... , d-1 ретті айырмалар стационарлық емес, ал ретті айырма стационарлы болса, онда уақыттық қатары ретті интеграцияланған уақыттық қатар болып табылады. Ол түрде жазылады. Стационарлық уақыттық қатар 0 ретті интеграцияланған уақыттық қатар деп саналады.

- ретті интеграцияланған уақыттық қатар болсын, ал - процессі, яғни

мұндағы . Онда жылжымалы орташаның авторегрессиялық интеграцияланған уақыттық қатары деп аталады.

15.3. Arima моделін идентификациялау

Уақыттық қатарды талдау кезінде моделінің реттерін анықтауда, модель коэффициенттерін бағалауда және қалдықтар дисперсиясын талдауда қиындықтар туады. Бокс-Дженкинс әдістемесі негізінде бір ғана байқау болатын берілген уақыттық қатар үшін, осы қатар тудыратын процессті лайықты түрде көрсете алатын, моделін құру әдісін ұсынады. Ол үш кезеңнен тұрады: идентификациялау, бағалау және адекваттылығын тексеру.

Модельді идентификациялау. Ең алдымен деректерді стационарлыққа тексеру қажет. Уақыттық қатардың графигі бойынша онда тренд, мезгілділік бар ма екенін байқауға болады.

Егер коррелограмма баяу төмендесе, онда уақыттық қатар стационарлық емес болады. Сонымен қатар бірлік түбірдің бар болуын тексеретін арнайы тест қолдануға болады.

Қатардың стационарлық немесе стационарлық емес екендігі анықталады. Екінші жағдайда тағы да айырмалары есептеліп, олар тағы да стационарлыққа тексеріледі. Нәтижесінде уақыттық қатардың интеграцияландыру реті анықталады. Экономикалық деректер үшін интеграцияландыру реті әдетте 0, 1, және өте сирек 2 сандарына тең болады.

Алынған стационарлық уақыттық қатар үшін таңдамалы ACF және PACF графиктері бойынша процессінің p, q реттері анықталады. Төменірек ретті модельдерді таңдап алған жөн. Ол үшін Акаике және Шварц критерийлерін қолдануға болады. ARMA процесстері үшін, оның құраушысы шексіз MA процесс ретінде көрсетілген және ол процессімен салыстырғанда жоғарырақ ретті барлық процесстерді қамтығандықтан, моделі таңдалады. Ал құраушысы шексіз AR процесс ретінде көрсетілген және ол процессімен салыстырғанда жоғарырақ ретті барлық процесстерді қамтиды.

Модельді бағалау. Таңдап алынған p, q реттерінің мәні үшін моделінің коэффициенттері бағаланады. q=0 болған жағдайда моделінің коэффициенттерін бағалау үшін ең кіші квадраттар әдісін қолдануға болады.

немесе моделдерін бағалау үшін ең кіші квадраттар әдісін қолдана алмаймыз. моделін қарастырайық:

, .

Оған қарапайым ең кіші квадраттар әдісін қолдану мүмкін емес, себебі мәндері белгісіз. Осы теңдеуді мерзім үшін жазайық:

Оны шамасына көбейтіп, алдыңғы теңдеуге қосамыз:

Осындай түрлендірулерді , , ... мерзім үшін қайталап, алатынымыз

мұндағы болғандықтан, қосылғышы бірте-бірте жоғалады. Геометриялық тізбек мүшелерінің қосындысының формуласын қолдана отырып теңдеуді келесі түрге келтіруге болады:

.

Бұл шексіз авторегрессиялық процесс. Мысалы оны ретпен шектейік, яғни

.

Регрессия теңдеуіндегі , параметрі сызықтық емес болғандықтан, оларды бағалау үшін ең кіші квадраттар әдісін қолдану мүмкін емес.

немесе модельдерінің коэффициенттерін бағалау үшін неғұрлым шындыққа ұқсас әдіс немесе ең кіші квадраттардың сызықтық емес әдісі сияқты, басқа әдістерді қолдануға болады.

Модельдің адекваттылығын тексеру. Құрылған моделі үшін келесілер орындалу керек:

- коэффициент бағалары мәнді болу керек, сәйкес -статистикалар абсолюттік шамасы жағынан, таңдап алынған мәнділік деңгейі үшін, Стьюдент үлестіруінің критикалық мәнінен аз болмау керек;

- қалдықтары на «ақ шуылға» ұқсас болу керек, яғни теория жүзінде ауытқулар үшін болғандықтан, статистикалық елеусіз автокорреляцияға ие болады.

және модельдерін да бағалауға болады. Жаңа енгізілген коэффициенттер мәнді болмау керек.

Өте көп байқау саны және жеткілікті үлкен үшін, уақыттық қатардың таңдамалық ACF

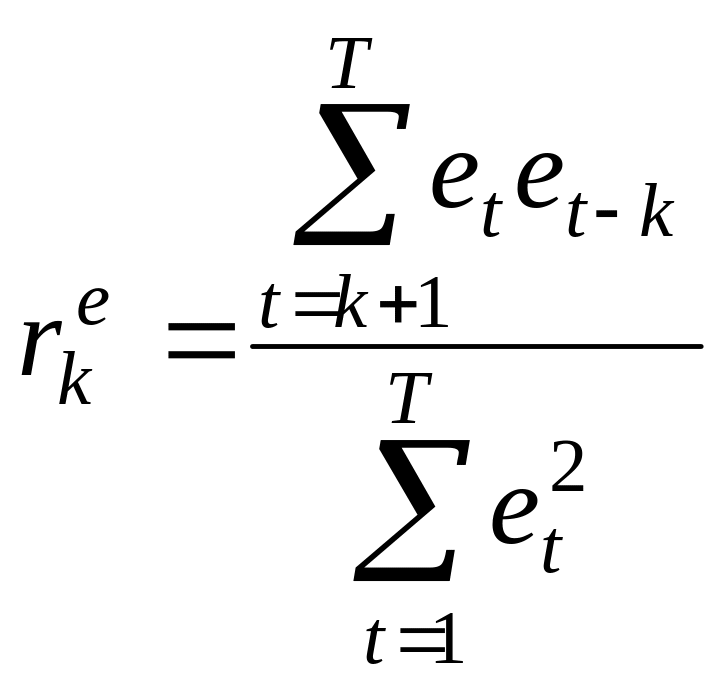
қалыптыға жақын үлестірге ие болады,

.

(бұл жерде 1,96 тең критикалық мән 2 санына дейін жуықталады) болған жағдайда, 5-пайыздық мәнділік деңгейде автокорреляция коэффициентінің нөлге теңдігі жайлы гипотезасы қабылданбайды.

қалдықтардың уақыттық қатары «ақ шуылға» сәйкес келу үшін, барлық мәндерінде автокорреляция коэффициентінің нөлге теңдігі жайлы гипотезасы жоққа шығарылмау керек.

Қалдықтардың автокорреляциялық функциясының алғашқы мәндері үшін осы гипотезаны тексеру Бокс-Пирстің -статистикасы арқылы жүзеге асады

.

Автокорреляцияның болмауы жайлы нөлдік гипотеза кезінде шамасы келесі үлестіруге ие болады . Егер шамасы критикалық мәннен асса, нөлдік гипотеза қабылданбайды.

Егер тест бойынша автокорреляцияның бар екендігі анықталса, онда таңдалған моделіне өзгерістер енгізу қажет. Мысалы, модельге сәйкес жылжымалы орташа компонентін енгізіп, мезгілдікті ескеру қажет болады.

Бастапқы деректерге бірнеше модельдер адекватты болатын жағдай да мүмкін болады. Онда модельді таңдауды Акаике

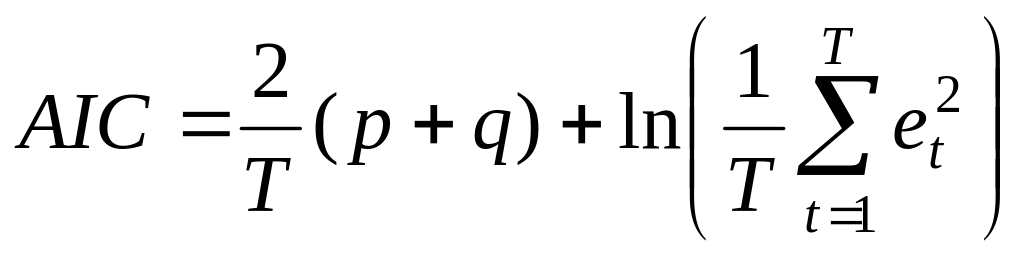
және Шварц

.

ақпараттық критерийлеріне сүйене отырып жүзеге асыруға болады,

Деректерге адекватты бірнеше модельдер ішінен және мәндері ең аз болатындай модельді таңдап алған жөн.

205