14.6 Сурет. Ма(2) процесстің коррелограммасы
Жалпы жағдайда процессінің автокорреляциялық функциясын көрсетуге болады
Мұнда
көрнекілік үшін
.
процессінің
автокорреляциялық функциясының
графигі
«нөлдік
емес» бағаналарды қамтиды.
14.4. Жылжымалы орташа моделінің ретін таңдау
процессінің
автокорреляциялық функциясы
мәннен бастап «үзілетіндіктен»
берілген уақыттық қатар үшін
мәнін анықтауға болады.
мәні
шамасы сол мәннен кейін нөлден мәнді
түрде ерекшеленбейтіндей таңдалады.
таңдамалы автокорреляциялық функция
келесі түрде анықталады:
.
үшін,
өте үлкен болған кезде таңдамалы
автокорреляциялық функция мәні жуықпен
қалыпты заңмен үлестіріледі, яғни
.
Келесі гипотезаларды құрайық:
және
.
Таңдап
алынған
мәнділік
деңгейі үшін
критикалық мәні стандартты қалыпты
үлестірілу кестесінен табылады. Мысалы,
5-пайыздық мәнділік деңгейі үшін
кездейсоқ щаманы стандартты қалыпты
үлестірілген кездейсоқ щамаға
түрлендіреміз
.
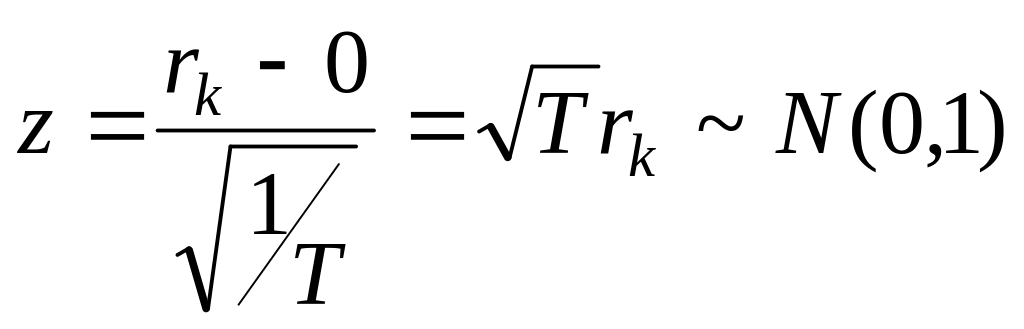Егер
болса,
мәнінің нөлге теңдігі жайлы
гипотеза жоққа шығарылады, ал егер
болса, гипотеза қабылданады. Бұл
жылжымалы орташа процессінің
ретін тәжірибе жүзінде анықтау әдісін
көрсетеді.
15. Жылжымалы орташаның авторегрессиялық интеграцияланған моделі
15.1. Arma процесстері
Бір айнымалылы процесстер AR және MA модельдерімен салыстырғанда күрделірек құрылымға ие болуы мүмкін. Егер авторегрессиялық процесстің
кездейсоқ мүшесін жылжымалы орташа процесспен алмастырсақ
,
онда
жылжымалы орташаның
авторегрессиялық
процессінің
моделін аламыз:
,
мұндағы .
Барлық
процессі шексіз
процессі немесе шексіз
процессі түрінде берілуі мүмкін.
Оңайлату үшiн бұл тұжырымды бiрiншi ретті авторегрессиялық процесс мысалында түсіндіреміз:
,
.
(15.1)
Стационарлық
шарты
орындалады
деп
есептелінеді.
мерзiм үшiн бұл теңдеудi келесі түрде
жазамыз:
,
мұндағы табылған мәнін бастапқы (15.1) теңдеуіне қоямыз:
.
(15.2)
Содан
соң (15.1) теңдеуін
мерзім үшін жазамыз да, алынған
мәнін (15.2) теңдеуіне қоямыз:
Сонымен әрi қарай жалғастыра отырып, келесі теңдеудi аламыз
,
(15.3)
үшін
бірінші қосылғыш
кезде нөлге ұмтылады. Алған теңдеу
шексiз
процесстi анықтайды.
Сонымен, бірінші ретті жылжымалы орташа процессін шексiз авторегрессиялық процессi түрiнде сипаттауға болатынын көрсетейік. процессі бар болсын:
,
.
(15.4)
(15.4) теңдеуін мерзім үшін жазамыз:
,
және
ондағы
мәнін (15.4) теңдеуіне қоямыз:
.
(15.5)
Енді
(15.4) теңдеуін
мерзім үшін жазамыз және ондағы
мәнін (15.5) қатынасқа қойып, келесі
теңдеуге келеміз
.
Осы
процедураны қайталай отырып (
деп есептейміз), соңында алатынымыз
.
(15.6)
Бұл шексіз авторегрессиялық процесс. Осыған ұқсас түрлендірулерді және процесстер үшін де жүргізуге болады. Ал процессі және құраушыларды қамтитындықтан, оны шексіз авторегрессиялық процесс немесе жылжымалы орташаның шексіз процессі ретінде көрсетуге болады.
процессін
қарастырамыз:
,
.
(15.7)
Математикалық
үмітін
,
дисперсияны
,
ковариацияны
,
,
есептейік.
Онда автокорреляциялық функция
,
(15.8)
,
(15.9)
процессі және процесстердің комбинациясы болғандықтан, оның автокорреляциялық функциясы авторегрессиялық процесс пен жылжымалы орташа процессінің қасиеттеріне белгілі бір шамада, ие болу керек.
процесс үшін автокорреляциялық функция 1 мерзім лагынан кейін «үзіледі», ал процессі үшін автокорреляциялық функцияның экспоненциалды кемуі орын алады. үшін (15.8)-(15.9) автокорреляциялық функциясын теоретикалық есептеу осындай тәртіпті көрсетеді. 15.1 суретте процессі тудырған, уақыттық қатардың таңдамалы автокорреляциялық функциясының графигі кескінделген. Үзік сызық, одан жоғары мәні нөлден мәнді түрде ерекшеленетін, деңгейді көрсетеді.
