14.4 Сурет. Авторегрессиялық процесстің таңдамалы acf коррелограммасы.

14.4 суреттегі жатық үзік сызықтар және деңгейінде жүргізілген, мұндағы - стандартты қалыпты үлестірудің критикалық мәні.

14.1 мысал. Қандайда бір авторегрессиялық процесстен туындайтын байқау саны бар уақыттық қатар бар болсын.

Авторегрессиялық процесс теңдеуінің ең кіші квадраттар әдісі бойынша бағаланған соңғы коэффициенті және -статистиканың сәйкес мәндері (14.1) кестесінде келтірілген. Авторегрессиялық процесстің ретін анықтау қажет.

5-пайыздық мәнділік деңгей үшін стандартты қалыпты үлестірудің критикалық мәні жуықпен 2-ге тең.

14.1 кестедегі деректер бойынша және үшін гипотезасы жоққа шығарылады, ал үшін қабылданатынын оңай көруге болады.

14.1 Кесте. Авторегрессияны бағалау нәтижелері

1	0,351	3,51
2	-0,268	-2,68
3	0,052	0,52
4	0,064	0,64
5	-0,047	-0,47
6	0,125	1,25
7	0,156	1,56
8	-0,077	-0,77
9	0,054	0,54

Бұдан авторегрессиялық процесстің реті 2 тең деп, яғни процесс болатыны жайлы қорытынды жасалады.

14.3. Жылжымалы орташа моделінің қасиеттері

Экономикада, авторегрессиялық процесс моделінде көрсетілген байланыстар құрылымынан басқа, бір айнымалылы уақыттық қатарлардағы басқа да байланыстар құрылымы кездеседі. Демек, қор нарығындағы акциялар бағасының өзгерісі келесі тәуелділікпен сипатталады:

, ,

мұндағы, - нөлдік математикалық үміті бар тәуелсіз кездейсоқ шамалар. Осы модельдің жалпы түрі жылжымалы орташа процессінің моделі болып табылады.

, . (14.7)

Осылай аталуының мағынасы ағымдық және алдыңғы ауытқулардың салмақталған қосындысы болғанында жатыр. Математикалық үміт

.

Әр түрлі мерзімдегі мәндерінің тәуелсіздігін ескере отырып дисперсияны анықтаймыз:

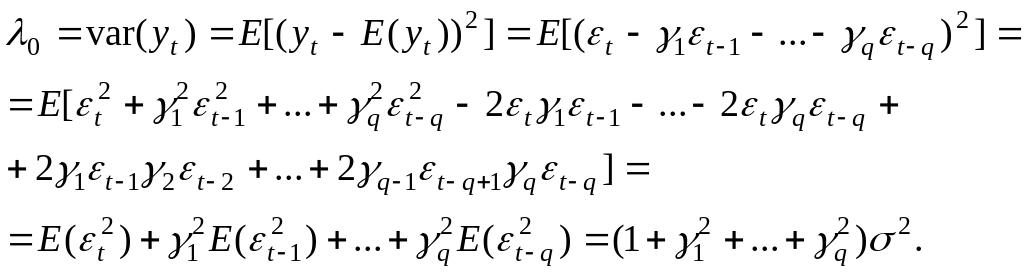
бірінші ретті жылжымалы орташа процессі:

, . (14.7)

Ол процесстің дисперсиясы болады. (14.7) түріндегі процессінің ковариациясын табайық:

Осыған ұқсас есептеулер жүргізе отырып,

үшін

болатынын оңай байқауға болады.

Демек , процессі үшін автокорреляциялық функциясы

14.5 Сурет. Болған жағдайда ма (1) процессінің коррелограммасы.

14.5 суреттегі автокорреляциялық функцияның коррелограммасында болғанда тек қана бір «нөлдік емес» бағана бар болады.

екінші ретті жылжымалы орташа процессі :

, . (14.8)

Оның дисперсиясы Ковариацияны табайық:

үшін .

жылжымалы орташа процессінің автокорреляциялық функциясы

Ол мәнінен бастап «үзіледі». Сондықтан, процесс коррелограммасында тек екі «нөлдік емес» бағана бар (14.6 сурет).