14. Авторегрессиялық модель және жылжымалы орташа моделі

14.1. Авторегрессиялық процесс қасиеттері

Айнымалының олардың алдыңғы мәндеріне тәуелділігін сипаттайтын қарапайым модельдер, ондаған және жүздеген теңдеулерді қамтитын үлкен эконометрикалық модельдермен салыстырғанда, сенімдірек болжамдар жасауға мүмкіндік беретіні байқалды. Демек бұл айнымалының болашақ мәндерін анықтайтын маңызды ақпарат оның өткен динамикасында жатқанын көрсетеді. Осындай модельдердің теориясын жасауға Г. Бокс және Г. Дженкинс зор үлес қосты.

11 бөлімде ұсынылған авторегрессиялық процессін қарастырайық:

, (14.1)

мұндағы . айнымалысы үшін стационарлық шарт орындалады деп саналады. Авторегрессиялық процесстердің қасиеттерін зерттеп, олардың автокорреляциялық функциясын салайық.

бірінші ретті авторегрессиялық процесс:

. (14.2)

(14.2) теңдеуінің екі жағының математикалық үмітін табайық. Стационарлық процесс анықтамасы мен шартын ескере отырып, табатынымыз

.

Сәйкесінше, осы (14.2) теңдеуінің екі жағының дисперсиясын есептеп келесі теңдеуді аламыз

.

Ковариацияның қасиеттерін пайдалансақ,

.

14.1 Сурет. Жағдайда ar(1) процессінің коррелограммасы.

Осы түрлендіруді рет қайталай отырып келесі қатынасты аламыз

,

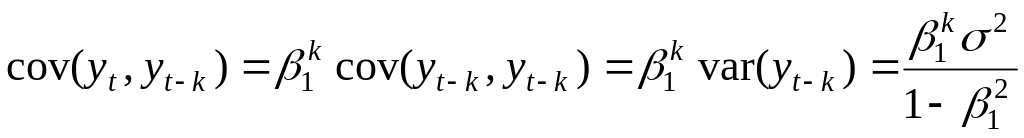яғни, үшін . шарты қажетті, әйтпесе процесс стационарлы болмайды және теріс мәнінің мағынасы жоқ. Енді автокорреляциялық функциясын есептеу оңайға түседі:

,

Коррелограмма түрі коэффициентінің таңбасына байланысты болады (14.1 және 14.2 суреттер).

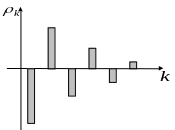
14.2 Сурет. Жағдайда ar(1) процессінің коррелограммасы.

Екі жағдайда да бағаналар биіктігі лаг шамасының өсуіне қарай экспонента бойынша төмендейді.

екінші ретті авторегрессиялық процесс:

, (14.3)

мұндағы кездейсоқ мүше . Бұл жолы да бірінші ретті авторегрессиялық процесстегідей, математикалық үмітті табамыз

.

Ковариация қасиеттерін ескеріп келесіні есептейміз

яғни келесі теңдікті аламыз Оның екі жағын шамасына бөлсек

(14.4)

, екенін ескерсек, үшін (14.4) теңдеуді келесі түрде жазуға болады:

(14.5)

Бұл екінші ретті авторегрессиялық процесс үшін Юл-Уолкер жүйесі . Оның шешімі

, .

14.3 Сурет. Характеристикалық теңдеудің кешенді түбірлері жағдайында ar(2) процессінің коррелограммасы.

Онда үшін басқа мәндері, екінші ретті айырмалық теңдеу болып табылатын (14.4) теңдеуден тізбекті түрде анықталады.

Егер характеристикалық теңдеудің түбірлері нақты сандар болса, стационарлық процесс үшін автокорреляциялық функция графигі 14.1 немесе 14.2 суреттегідей, ал егер характеристикалық теңдеу түбірлері комплекстік сандар болса, онда графигі экспоненциалды амплитудасы кемімелі синусоида (14.3 сурет) түрінде болады.

14.2. Авторегрессиялық процесс моделінің реті

және арасындағы дербес автокорреляция, аралық мүшелерімен сызықтық түсіндірілетін бөлігін алып тастағандағы, және арасындағы қарапайым автокорреляция ретінде табылады.

Анықтама бойынша дербес автокорреляциялық функция , яғни және арасында аралық мүшелер жоқ болғандықтан, .

(14.1) сызықтық теңдеумен берілген, авторегрессиялық процессі болсын. Онда дербес автокорреляциялық функцияның мәні

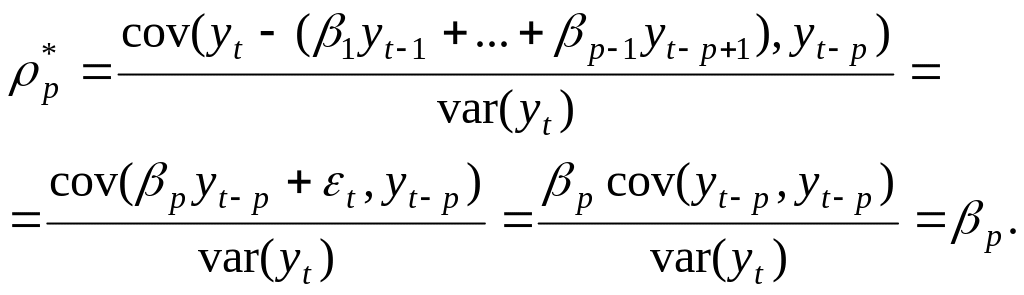
авторегрессиялық процессі келесі қасиеттерге ие болады: ол үшін бастап, барлық дербес автокорреляциялық функциялардың мәні нөлге тең.

ретті авторегрессиялық процесс теңдеуінде мәні соңғы коэффициентіне тең болады. процессінің Юл-Уолкер жүйесін жазайық:

(14.6)

(14.6) сызықтық теңдеулер жүйесінің анықтауышы нөлге тең емес екенін тексеруге болады. Сондықтан оның шешімі Крамер ережесі арқылы анықталады. Қазіргі жағдайда келесі мән қызығушылық туғызады

,

мұндағы анықтауыш анықтауышының соңғы тік жолын (14.6) теңдеулер жүйесінің сол жағындағы тік жолмен алмастыру арқылы алынады, яғни

.

процессі үшін аталған қасиетті тексереміз. Ол процесс үшін автокорреляциялық функция , , шартына бағынады. анықтауышының соңғы тік жолы оның алғашқы тік жолын мәніне көбейткенге тең болатыны анық. Бұл анықтауышының тік жолдары сызықтық тәуелді, сондықтан нөлге тең екендігін көрсетеді. Демек, кез-келген үшін .

процессін қарастырайық. Бұл процесс үшін (14.4) қатынас ақиқат болғандықтан, анықтауышындағы соңғы тік жол бірінші және екінші тік жолдарының сызықтық комбинациясы болып табылады. Демек, анықтауыштың тік жолдары сызықтық тәуелді, ал анықтауыш . Крамер ережесіне сәйкес кез-келген үшін .

процессі үшін анықтауышының соңғы тік жолы оның алғашқы тік жолдарының сызықтық комбинациясы болып табылады, соның салдарынан және , яғни кез-келген үшін .

Тәжірибе барысында уақыттық қатары қандай стохастикалық процесстен туындайтыны белгісіз. Мысалы, ол қандайда бір авторегрессиялық процесстен туындады делік. Оның ретін анықтау қажет. Оны мәнінен бастап дербес автокорреляциялық функцияның мәні нөлге дейін «үзіледі» деген қасиетіне сүйене отырып жүзеге асыруға болады.

Таңдамалы дербес автокорреляциялық функция үшін аталған қасиет дәл орындала қоймайды. Бірақ, ол жуықпен орындалады деп санауға болады. нөмірінен бастап таңдамалы мәні

,

мұндағы, және - сәйкес және регрессия қалдықтары, модулі бойынша жеткілікті аз болады.

Таңдамалы автокорреляциялық функцияның мәні, ең кіші квадраттар әдісі бойынша, келесі авторегрессиялық процесс теңдеуінің соңғы коэффициентінің бағасы ретінде анықталады

.

- ретті авторегрессиялық процесс болсын. Өте үлкен үшін ең кіші квадраттар әдісі бойынша бағасы жуықпен

үшін .

Авторегрессия ретін бағалау үшін келесі статистиканы қолдануға болады

.

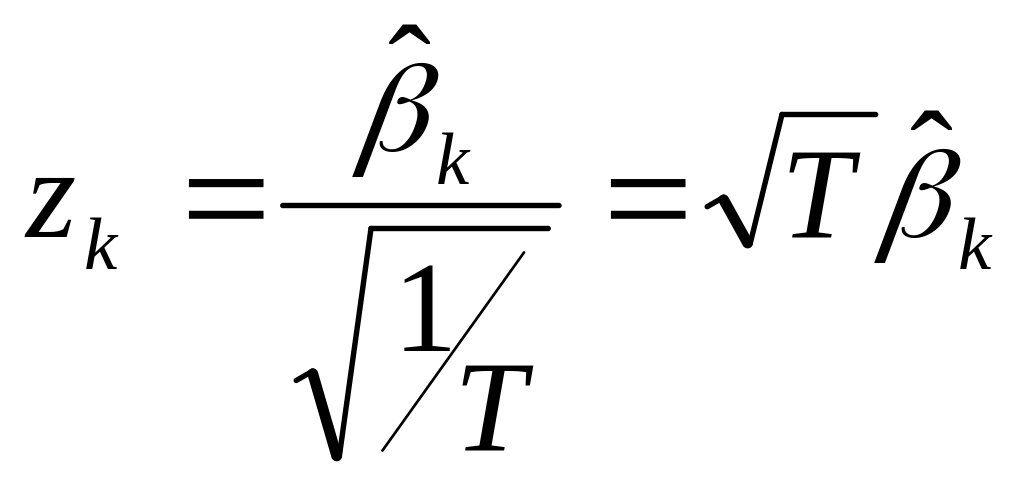Оның көмегімен мына гипотезалар тексеріледі

және .