10. Дисперсия. Определение и свойства.

Определение: Диспе́рсия (рассеяния)случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания.

Наз-ют МО квадрата отклонения случайной велечины её мО.

D(X)=M[X-M(X)]^2

Дисперсия= разностимежду мат.ожид.квадрата случайной елечины Xи квадратом её МО:

D(X)=M(X^2)-[M(X)]^2

Свойства: 1: дисперсияпостоянной велечины С = 0 D(C)=0

2:Постоянный множитель можно выносить за знак дисперсии, возводя его вквадратD(CX)=C^2D(X)

Сво-во:3 Дисперсия суммы двух независимых случайных велечин = сумме дисперсий этих велечин:D(X+Y)=D(X)+D(Y)

Сво-во 4: Дисперсия разности двух независимых случайных велечин равна сумме их дисперсий D(X-Y)=D(X)+D(Y)

11. Функция распределения непрерывной случайной величины. Плотность вероятности непрерывной случайной величины.

Фун-е распределении наз-ют фун-ю F(x) , определяющую вероятность того, что случайная велечина Х в результате испытания примет значение, меньше х. т.е F(x)=P(X<x)

Геометрически это равенсто можно истолковать так:F(x) есть вероятность того, что случайная велечина примет, значение,которое изображается на оси точкой, лежащей левее точки х.

• Можно дать более точное опр. Непрерывной случ. Велечине:случ. Велечину называют непрерывной, если ее фун-я распределения есть непрерывная, кусочно-дифференцируемая фу-я с непрерывной производной.

Свой-ва Фун-и распре-я.

1: Значение фун-и расп-я принадлежит отрезку[0;1]

2:F(x)-неубывающая фун-я.т.е F(x₂)>=F(x₁), если х2>x1.

3:Если возможные значения случайной велечины принадлежат интервалу (a,b) то 1)F(x)=0 При x<=а2) F(x)=1 Прих>=b

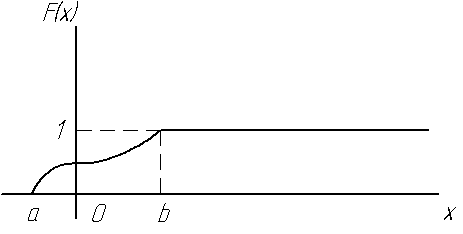
Плотность вероятности непрерывной случайной величины.

Плотностью распределения вероятностей непрерывной случайной велечиныХ называют фун-ю f(x)-первую производную от функции распределения F(x)

F(x)=F^(x)  что фун-я распределения является первообразной для плотности распределения.

Св-во1:Плотность рас-я – неотрицателььная фун-я f(x)>=0

2:Несобственной интегралл от плотности распределения в пределах от – бесконеч. До бесконеч = 1

12: Нормальное распределение. Влияние параметров на функцию плотности вероятности.

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывает плотностью:

Мы видим, что нормальное рапределение опеделяется двумя параметрами: a и Q а- МО, Q- среднее квадратичное нормального распределения.

13. Асимметрия и эксцесс распределения.

Ассиметрией теоретического распеределения называютотношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

As=

Ассиметрия положительна, если «длинная часть» кривой распределения расположена справа от МО, асииметрия отрицательна, если Длинная чать кривой расположена слеваот МО.

Эксцессом теоретического распределения называют характеристику, которая определяет равенством

14. Условное математическое ожидание.

Условной МО дискретной случайной велечины Y при X=x(x-определенное возможное значеное Х) называют произведение возможных значений Y на их условные вероятноти.