5. Обтекание кругового цилиндра с циркуляцией.

Наложим на обтекание кругового цилиндра плоский вихрь (циркуляционный поток) с центром в начале координат (1.1.14).

Потенциал суммарного течения будет иметь вид

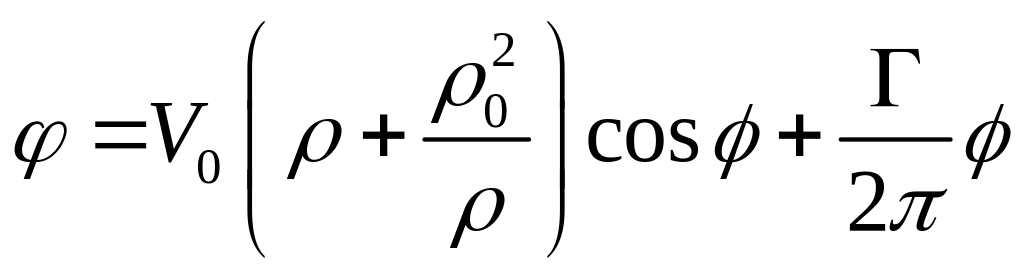, (1.3.1)

а функция тока

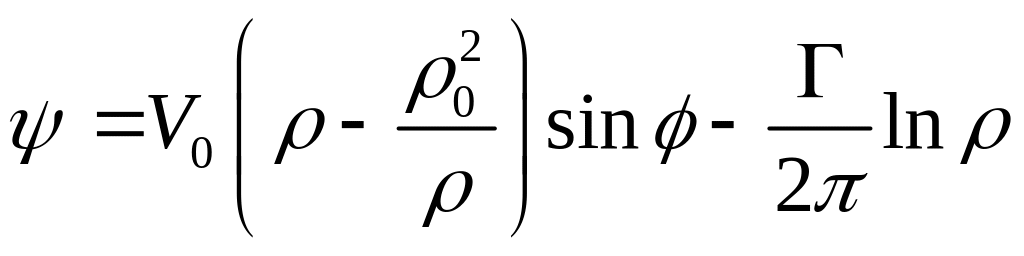. (1.3.2)

Получим выражения для скоростей этого потока

, (1.3.3)

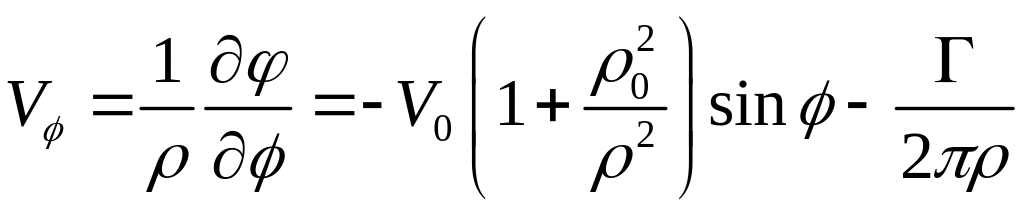. (1.3.4)

Из формулы (1.3.3) видно, что добавление плоского вихря не влияет на величину радиальной скорости, и, соответственно, не нарушает условие непротекания на поверхности цилиндра, где выражения для скоростей принимают вид

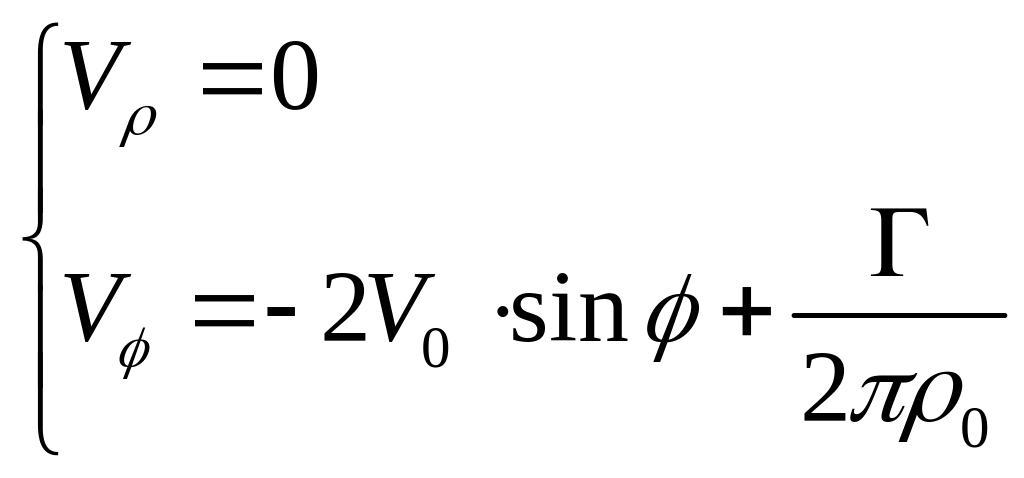. (1.3.5)

Найдем положение критических точек на поверхности цилиндра. В критических точках скорость равна нулю, откуда получим

;

(1.3.6)

В зависимости от величины циркуляции  возможны четыре варианта решения уравнения (1.3.6):

1) ; ;

, ,

получаем бесциркуляционное обтекание цилиндра (п.1.2, рис.5);

2) ; ;

например, при получаем ;

, - такое течение изображено на рис.6;

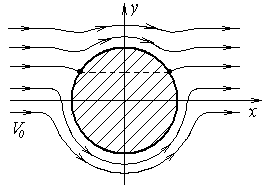
Рис. 5

3) ; ;

- течение с одной критической точкой (рис.7);

Рис. 6

4) ;

решения не существует, следовательно, на поверхности цилиндра нет критических точек. Такое течение изображено на рис.8, где видно, что критическая точка расположена выше цилиндра, а часть примыкающей к цилиндру жидкости вовлечена во вращательное движение.

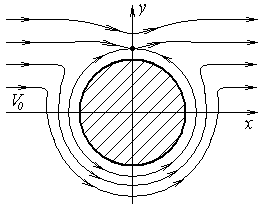
Рис. 7

Рассмотрим случай 2) более подробно. При этом варианте течения скорость на верхней части цилиндра при

, (1.3.7)

а по нижней стороне цилиндра при

, (1.3.8)

то есть в симметричных точках . Коэффициент давления на верхней и нижней сторонах цилиндра также будет разным

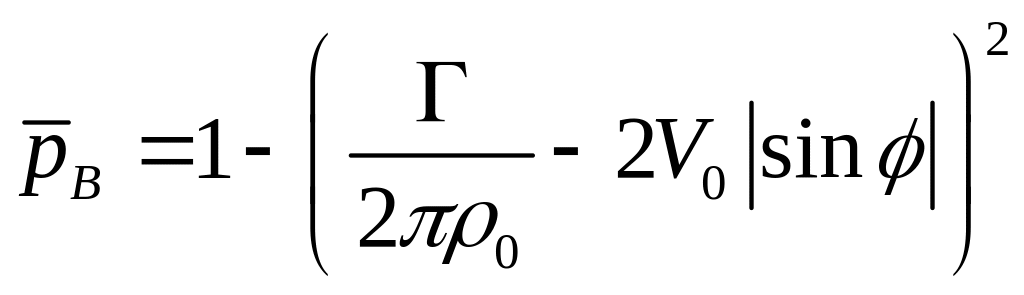, (1.3.9)

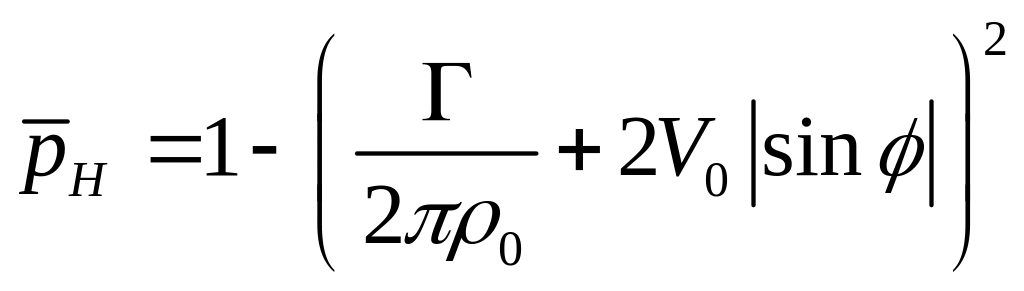, (1.3.10)

причем в соответствующих точках ( ) , что при интегрировании давлений по поверхности цилиндра даст гидродинамическую силу .

Получим выражение для R_y. Рассмотрим элемент площади поверхности цилиндра

.

К этой площади приложено избыточное давление

.

Элементарная сила избыточного давления, действующая на площадь dS, выражается в виде

,

причем на окружности , а знак «минус» появляется, так как сила направлена внутрь цилиндра, а нормаль – наоборот.

Элементарная вертикальная сила записывается в виде

.

Проинтегрируем dR_y по поверхности цилиндра

,

где  - плотность жидкости, а коэффициент давления имеет вид

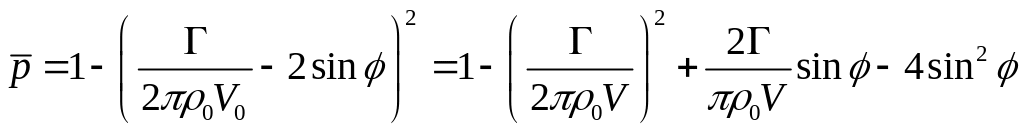Подставим это выражение в формулу для R_y:

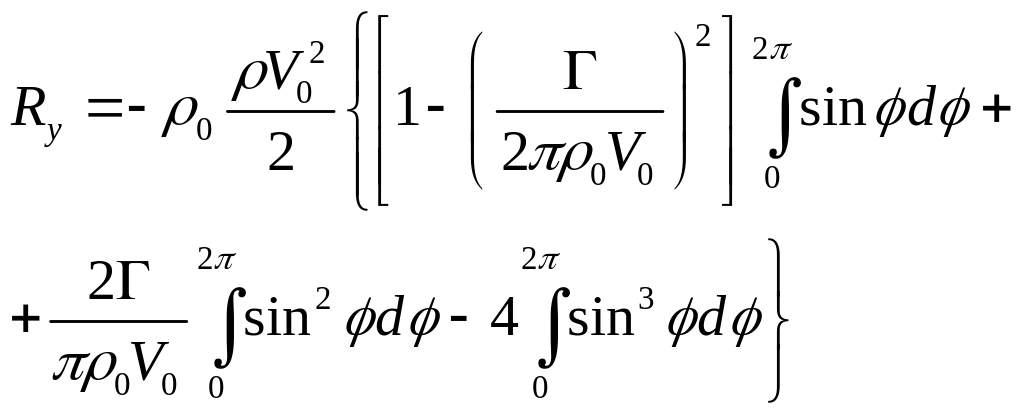
После необходимых вычислений получим выражение для подъемной силы при обтекании цилиндра с циркуляцией

. (1.3.11)

Направление силы перпендикулярно скорости набегающего потока. Для того, чтобы определить это направление, необходимо повернуть вектор скорости набегающего потока на 90⁰ против направления циркуляции. При этом необходимо учитывать, что при вращении жидкости против часовой стрелки циркуляция принимается положительной.

6. Обтекание сферы.

Обтекание сферы потоком невязкой жидкости со скоростью V₀ может быть получено наложением поступательного потока (1.1.8) на поток, генерируемый пространственным диполем (1.1.20).

Потенциал суммарного течения будет иметь вид

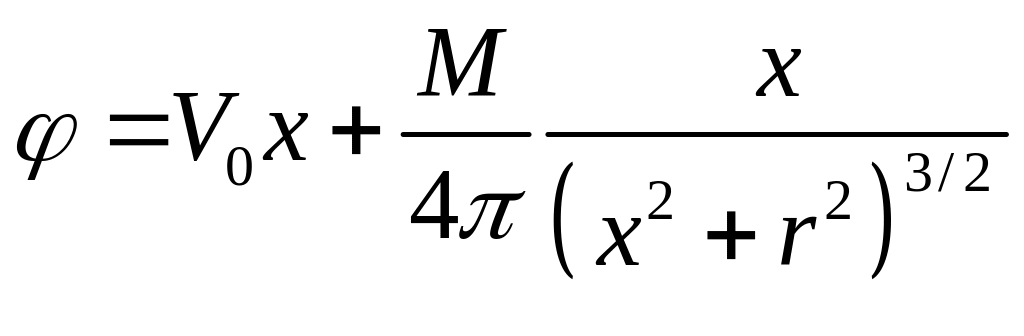, (1.7.1)

при этом потенциал обтекания диполя  можно представить в виде суммы потенциала набегающего потока и потенциала вызванных скоростей _в:

. (1.7.2)

Функция тока суммарного течения также может быть получена путем сложения функций тока диполя и набегающего потока

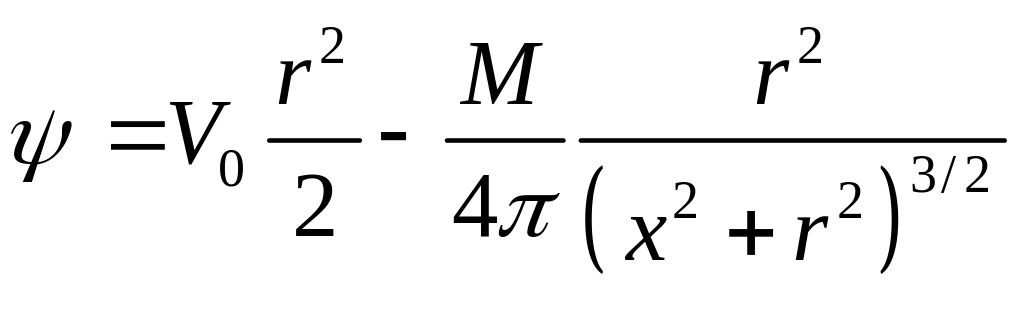. (1.7.3)

Момент диполя M пока остается неопределенной величиной. Найдем выражения для линий тока (точнее, это будут поверхности тока). Для этого приравняем функцию тока константе. Если эту константу взять равной нулю, то мы получим уравнение нулевой линии тока, которое будет иметь вид

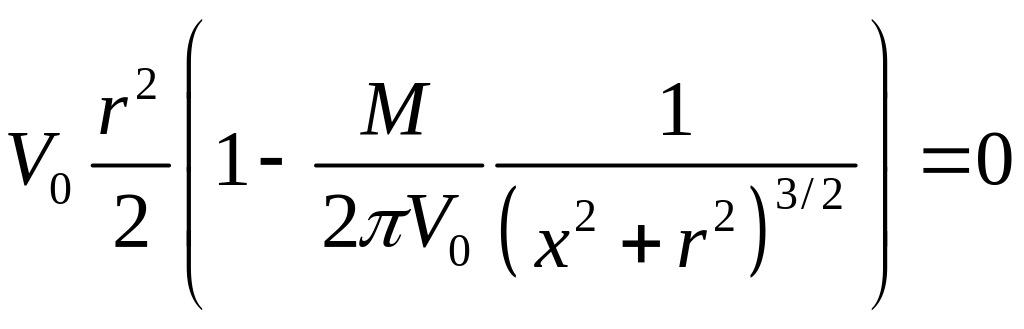(1.7.4)

Это уравнение имеет два корня: первый корень ­­r=0 соответствует оси x, второй корень

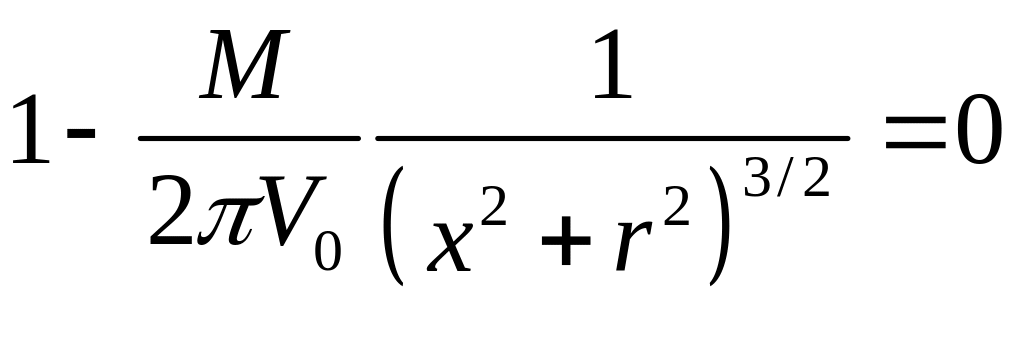. (1.7.5)

Выражение (1.7.5) можно записать немного иначе, если перейти в сферическую систему координат. При этом , тогда второй корень уравнения (1.7.4) запишется в виде или 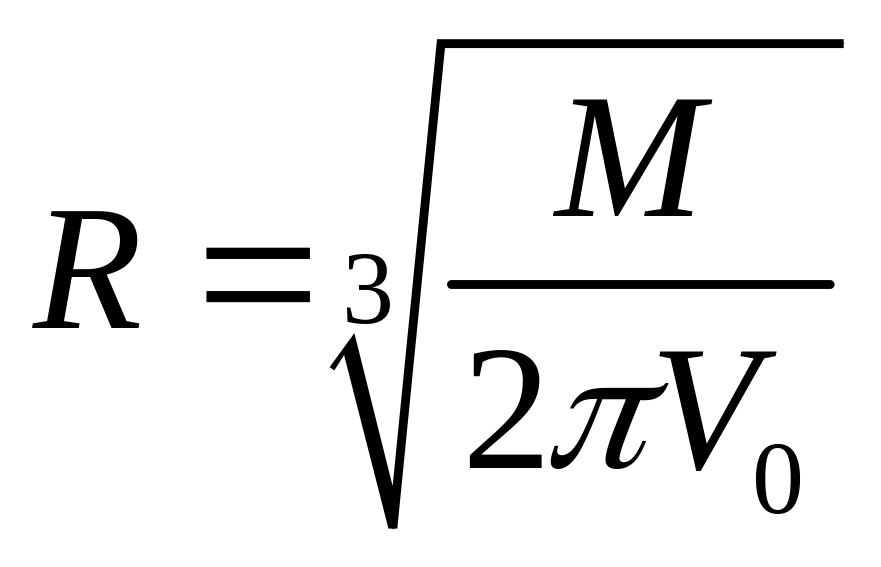. Так как подкоренное выражение является постоянной величиной, то если обозначить 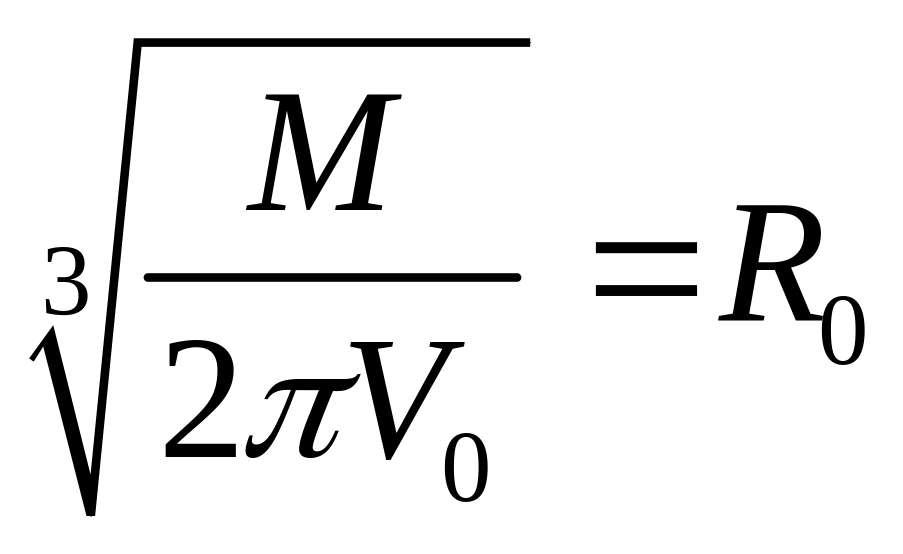, мы получим выражение для сферы радиусом R₀. Таким образом, нулевая поверхность тока состоит из оси x и поверхности сферы радиусом R₀.

Заменим часть поверхности тока, соответствующую сфере, твердой стенкой. В силу того, что на поверхности тока и на твердой стенке в невязкой жидкости выполняется одно и то же граничное условие непротекания, такая замена не повлияет на течение жидкости вне сферы, и мы получим обтекание невязкой жидкостью сферы радиусом R₀. При этом связь между радиусом сферы и моментом диполя M будет иметь вид

.

Подставляя эту зависимость в выражение для потенциала течения (1.7.1) и переходя к сферическим координатам, получим потенциал обтекания сферы заданного радиуса

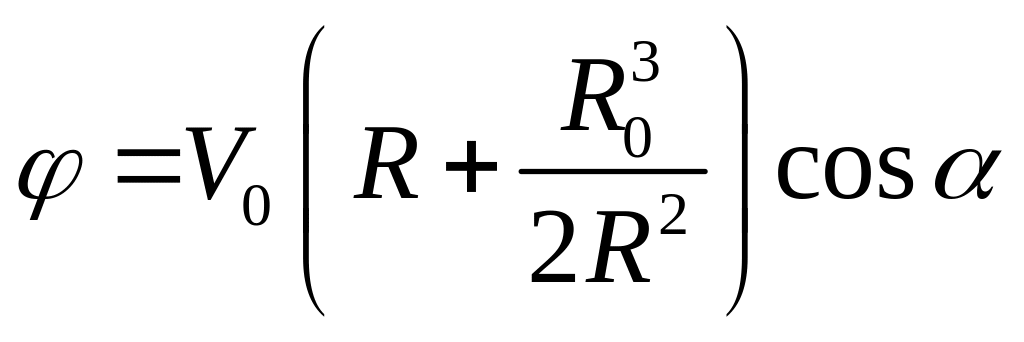. (1.7.6)

Из (1.7.6) можно получить проекции скоростей при обтекании сферы

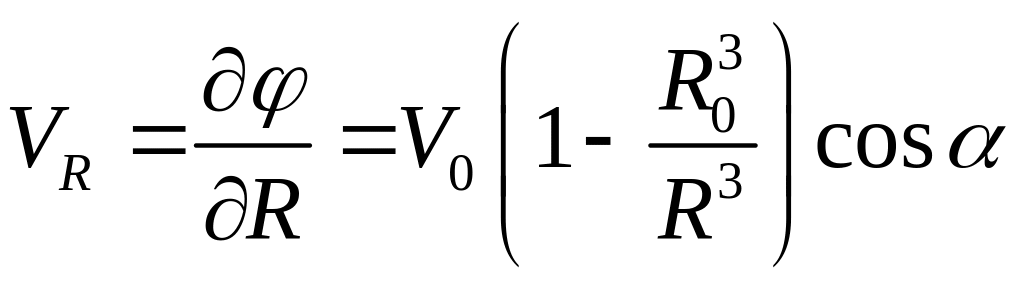, (1.7.7)

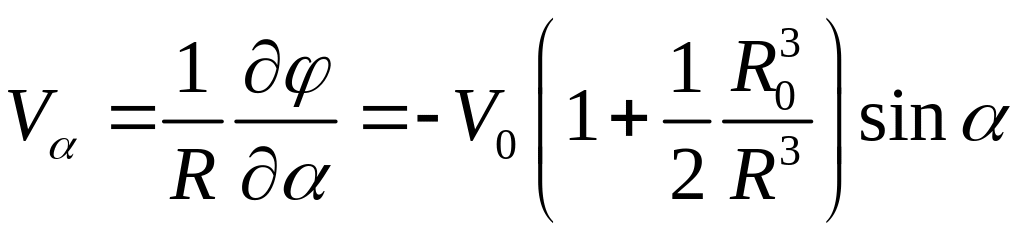. (1.7.8)

Подставляя в эти формулы R=R₀, получим скорости на поверхности сферы

, . (1.7.9)

Полная скорость на поверхности сферы

, (1.7.10)

а коэффициент давления на сфере

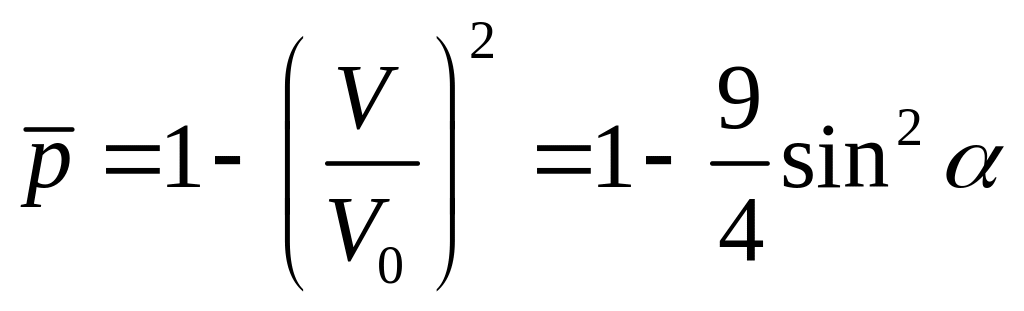. (1.7.11)