Особенности функции Лагранжа неусредненной задачи при базовых значениях решений. Методы решения задач оптимизации в среднем.
Поиск решения матричных игр с использованием смешанных стратегий. Методы поиска оптимальных смешанных стратегий.
Найти кратчайший путь в сетевом графике с использованием метода динамического программирования.
Заведующий кафедрой ТКА А.Э. Софиев
«___»______________ 20 г.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Московский Государственный Машиностроительный Университет
Институт Инженерной Экологии и Химического Машиностроения
Кафедра ТКА
Дисциплина «Теория автоматического управления»
Курс 4
Экзаменационная сессия 2012 – 2013 уч. Года Экзаменационное задание №11
Метод неопределенных множителей Лагранжа. Метод штрафных функций.
Метод динамического программирования. Принцип Беллмана. Уравнение и функция Беллмана (пояснить на примере поиска кратчайшего пути в сетевом графике).
Привести формализованную постановку задачи оптимизации (идентификации параметров математической модели, определение оптимальных настроек регуляторов).
Заведующий кафедрой ТКА А.Э. Софиев
«___»______________ 20 г.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Московский Государственный Машиностроительный Университет
Институт Инженерной Экологии и Химического Машиностроения
Кафедра ТКА
Дисциплина «Теория автоматического управления»
Курс 4
Экзаменационная сессия 2012 – 2013 уч. Года Экзаменационное задание №12
Формализованная постановка задачи линейного программирования. Примеры задач линейного программирования (задача об оптимальной диете, транспортная задача).
Понятие о вариационной задаче. Примеры вариационных задач. Их особенности.
Привести алгоритм решения конкретной задачи многостадийной оптимизации методом динамического программирования. Выполнить два-три этапа поиска (на примере задачи о коммивояжере).
Заведующий кафедрой ТКА А.Э. Софиев
«___»______________ 20 г.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Московский Государственный Машиностроительный Университет
Институт Инженерной Экологии и Химического Машиностроения
Кафедра ТКА
Дисциплина «Теория автоматического управления»
Курс 4
Экзаменационная сессия 2012 – 2013 уч. Года Экзаменационное задание №13
Возможный алгоритм поиска решения задачи многостадийной оптимизации с использованием дискретного принципа максимума (на основе метода локального исключения зависимых переменных).
Метод штрафных функций.
Решить задачу оптимального распределения нагрузок.
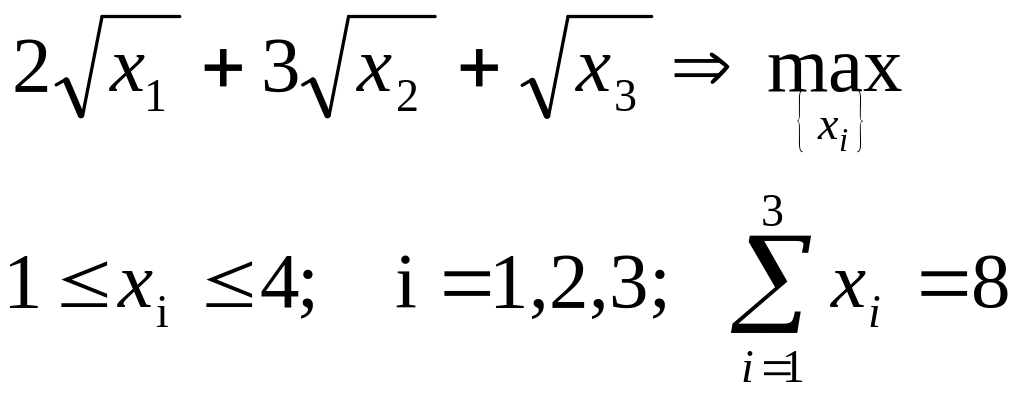
Заведующий кафедрой ТКА А.Э. Софиев
«___»______________ 20 г.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Московский Государственный Машиностроительный Университет
Институт Инженерной Экологии и Химического Машиностроения
Кафедра ТКА
Дисциплина «Теория автоматического управления»
Курс 4
Экзаменационная сессия 2012 – 2013 уч. Года Экзаменационное задание №14
Метод динамического программирования. Особенности постановки задач, для решения которой он применим. Принцип Беллмана (проиллюстрировать на примере задачи поиска кратчайшего пути в сетевом графике). Уравнение и функция Беллмана.
Изопериметрическая задача. Условия оптимальности для нее.
Дать постановку и привести решение изопериметрической задачи на примере задачи максимизации прибыли предприятия с учетом ненакопления продукции на складе.
Заведующий кафедрой ТКА А.Э. Софиев
«___»______________ 20 г.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Московский Государственный Машиностроительный Университет
Институт Инженерной Экологии и Химического Машиностроения
Кафедра ТКА
Дисциплина «Теория автоматического управления»
Курс 4