9. Рассмотрим условие устойчивости линейных систем.
Решение Yсв(t) однородного дифференциального уравнения имеет вид:
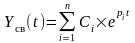, (2.16.2)
где
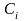
постоянные интегрирования, определяющиеся
начальными условиями и возмущением; рi
корни характеристического уравнения.
Комплексным корням рi соответствуют колебательные переходные процессы, действительным корням рi апериодические переходные процессы.
Для того чтобы свободная составляющая затухала (система была устойчива), действительные части всех корней рi должны быть отрицательными. Если хотя бы один из корней имеет действительную положительную часть, то система неустойчива. Если все корни рi мнимые, то система находится на границе устойчивости.
Изобразим корни на комплексной плоскости и получим следующее правило. Устойчивой системе соответствуют левые корни характеристического уравнения, неустойчивой правые.
Поскольку решение уравнений высокого порядка сопряжено с определенными трудностями, то анализ устойчивости линейных систем проводится по алгебраическим и частотным критериям. Наиболее часто используют алгебраический критерий Гурвица и частотный критерий Найквиста.
2-е вопросы
1.Передаточные функции систем автоматического регулирования
А. Передаточная функция САР по управляющему воздействию определяет взаимосвязь между изменением регулируемой величины Y и изменением управляющего воздействия Yз:
;
Б. Передаточная функция САР по возмущающему воздействию определяет взаимосвязь между изменением регулируемой величиной Y и изменением возмущающего воздействия F:
.
В. Передаточная функция САР для ошибки по управляющему воздействию определяет взаимосвязь между изменением ошибки еy и изменением задающего воздействия Yз:
Г. Передаточная функция САР для ошибки по возмущающему воздействию определяет взаимосвязь между изменением ошибки е и изменением возмущающего воздействия F:
2. Оценка точности линейных сар
Статическим звеном называют звено, не содержащее интегрирующих звеньев, последовательно соединенных со всеми другими звеньями, входящими в звено.
Статической системой называют систему в разомкнутом состоянии представляемую статическим звеном:
Wc.p = Wc .
Оценка точности в статических режимах
В статических режимах точность оценивают статическими ошибками по управляющему еу и возмущающему еF воздействиям, которые находятся по передаточным функциям (2.13.4) и (2.13.5) с учетом вида передаточных функций разомкнутых систем (2.15.3) и (2.15.4).
Для статических систем имеем:
;
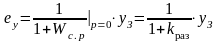(2.15.5)
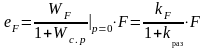, (2.15.6)
где
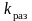
коэффициент передачи разомкнутой
системы (для общего вида (2.15.1)
это k0
);
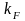
коэффициент передачи звена WF
.
Случай, когда звено WF является астатическим, не рассматривается, поскольку ошибка превращается в бесконечность, система оказывается неработоспособной и не может быть в таком виде реализована.
3. Оценка точности при гармонических воздействиях
Пусть управляющее воздействие или возмущающее воздействие на систему изменяются по гармоническому закону:
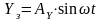; (2.15.10)
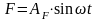. (2.15.11)
Тогда ошибка системы также будет меняться по гармоническому закону:
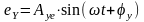; (2.15.12)
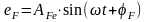, (2.15.13)
где
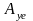и
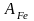
амплитуды ошибок по управляющему и
возмущающему воздействиям.
Амплитуды ошибок могут быть найдены как произведения Yз и F на модули соответствующих передаточных функций (2.13.3), (2.13.5) для ошибок:
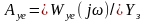; (2.15.14)
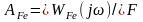. (2.15.15)
Для следящих систем важным показателем также является разность фаз между заданным и действительными значениями регулируемой величины:
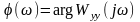. (2.15.16)
Чем меньше (), тем лучше качество регулирования.