1. Передаточная функция САР по управляющему воздействию определяет взаимосвязь между изменением регулируемой величины Y и изменением управляющего воздействия Y_з:

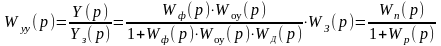; (2.13.1)

где W_п(p)  передаточная функция прямой цепи системы; W_р(p)  передаточная функция разомкнутой системы.

При выводе передаточной функции (2.13.1) воспользовались (2.12.1) и (2.12.3).

2. Передаточная функция САР по возмущающему воздействию определяет взаимосвязь между изменением регулируемой величиной Y и изменением возмущающего воздействия F:

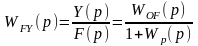. (2.13.2)

При выводе (2.13.2) исходную структурную схему для наглядности можно преобразовать к виду, представленному на рис. 2.13.2. При таком преобразовании учитывали то, что Y_з = 0 и поэтому звено W_з можно исключить.

3. Передаточная функция САР для ошибки по управляющему воздействию определяет взаимосвязь между изменением ошибки е_y и изменением задающего воздействия Y_з:

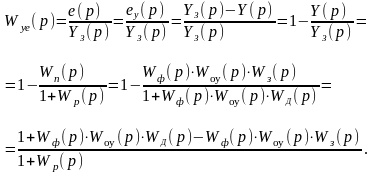
(2.13.3)

Коэффициенты передачи датчика и задатчика равны друг другу, поскольку Y_з и Y должны быть представлены в одном масштабе. Поэтому, если пренебречь инерционностью датчика и задатчика или считать их динамические свойства приблизительно одинаковыми, то W_з = W_Д и передаточная функция (2.13.3) приобретает вид:

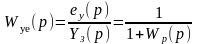. (2.13.4)

Форма 2.13.4 особенно удобна для исследования статических ошибок, когда инерционность звеньев системы не имеет значения.

4. Передаточная функция САР для ошибки по возмущающему воздействию определяет взаимосвязь между изменением ошибки е и изменением возмущающего воздействия F:

.

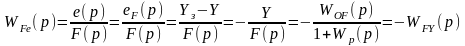5. Понятие об оценке качества регулирования

Качество регулирования оценивают тремя группами показателей.

1. Точность. Точность регулирования оценивают группой показателей, характеризующих отклонение регулируемой величины от заданного значения в установившихся режимах.

2. Устойчивость. Устойчивость характеризует способность системы возвращаться в исходный или близкий к нему установившийся режим после снятия воздействия, вызвавшего выход из установившегося режима.

Неустойчивые системы неработоспособны.

Устойчивость оценивают специально разработанными критериями. Устойчивость также можно оценить по переходным процессам системы, полученным, например, путем моделирования на ЭВМ.

3. Качество переходных процессов. Качество работы систем в переходных (неустановившихся) режимах оценивают группой показателей, характеризующих быстродействие системы, колебательность переходных процессов и отклонение регулируемой величины в неустановившихся режимах от заданного значения. Существуют также интегральные критерии, позволяющие оценить качество работы в среднем за время регулирования.

В последующих параграфах будут рассмотрены некоторые наиболее часто используемые показатели качества регулирования.

6.Статическим звеном называют звено, не содержащее интегрирующих звеньев, последовательно соединенных со всеми другими звеньями, входящими в звено.

Статические звенья имеют статические характеристики.

Передаточная функция линейного статического звена имеет вид:

.

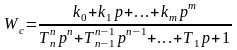Статической системой называют систему в разомкнутом состоянии представляемую статическим звеном:

W_c.p = W_c .

7.Астатическим звеном называют звено, содержащее интегрирующие звенья, последовательно соединенные со всеми другими звеньями, входящими в звено.

Передаточная функция линейного астатического звена имеет вид:

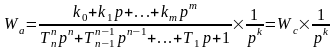
Астатической системой называют систему в разомкнутом состоянии, представляемую астатическим звеном:

,

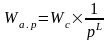где L  степень астатизма системы.

8. Устойчивость  это свойство системы возвращаться в исходный или близкий к нему установившийся режим после снятия воздействия, вызвавшего выход из установившегося режима.

Выходная величина устойчивой системы остается ограниченной в условиях действия на систему ограниченных по величине воздействий.

Неустойчивая система является неработоспособной, поэтому проверка устойчивости является обязательным этапом анализа системы, а обеспечение устойчивости  обязательным условием синтеза.

В общем случае качество нелинейных систем зависит от величины воздействий. Системы устойчивые при одних воздействиях могут быть неустойчивы при других воздействиях. В связи с этим существуют понятия устойчивости в малом, в большом и в целом (абсолютная устойчивость).

Устойчивость в малом  устойчивость при бесконечно малых отклонениях от исходного режима.

Устойчивость в большом  устойчивость при конечных отклонениях от исходного режима, возможных в данной системе по условиям работы.

Устойчивость в целом  устойчивость при неограниченных отклонениях.

В линейных системах таких градаций устойчивости не существует. Линейная система либо неустойчива, либо находится на границе устойчивости, либо устойчива в целом. При этом будут устойчивы не только положения равновесия системы, но и любые вынужденные процессы.