
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования « Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»
Физико-технологический институт
Кафедра «Физические методы и приборы контроля качества»
Физика твердого тела
Отчет
по лабораторной работе №5:
«Изучение фазового перехода второго рода»
Преподаватель: Зацепин А.Ф.
Студенты группы Фт-300602: Александренко А.М.
Исаченко Л.Е.
Камалова А.Ф.
Коробельникова А.А
Романова М.В.
Серкова Т.О.
Тарасова Е.А.
Третьяков М.В.
Яблокова А.А.
Екатеринбург 2012
1. Цель работы.
1.1. Ознакомление с методами изучения фазового перехода на примере сегнетоэлектрика ТГС.
1.2. Экспериментальное определение температурной зависимости параметра упорядочения при фазовом переходе второго рода и вычисление коэффициента в разложении Ландау.
2. Исследуемые приборы.
При выполнении работы используются: блок задания переполяризующего напряжения, осциллограф, самописец, программируемый калькулятор МК-46, а также кассета с исследуемым образцом.
3. Теоретическая часть
3.1 Сегнетоэлектрики - нелинейные диэлектрики. Они обладают широкими функциональными возможностями, связанными с существованием в них пиро-, пьезоактивности, высокой диэлектрической проницаемости, электрооптического эффекта. На основе этих кристаллов создаются приемники инфракрасного диапазона, акустические и гидроакустические устройства, системы акустооптики, акустооптоэлектроники, оптической связи и локации, преобразователи света, параметрические усилители сверхвысокочастотного диапазона и т.д.
3.2 . Вещество в твердом состоянии может находиться в различных фазах, соответствующих равным кристаллическим модификациям. Это явление называется полиморфизмом. В каждой фазе кристалл характеризуется определенной симметрией в расположении атомов вещества. Изменение симметрии приводит к изменению его физических свойств. Устойчивость данной кристаллической модификации связана с энергетической выгодностью того или иного расположения структурных элементов. При изменении внешних условий (температуры, механических напряжений, электрического поля) возможна спонтанная перестройка элементов структуры - фазовый переход.
Различают фазовые переходы первого и второго рода. Фазовые переходы первого рода характеризуются скачкообразным изменением кристаллической структуры. При этом физические свойства представляющие первую производную от термодинамического потенциала также изменяются скачком: энтропия, объем, электрическая поляризация, магнитная индукция и др. В случае фазовых переходов второго рода расположение атомов изменяется непрерывным образом, непрерывно изменяются первые производные, но терпят разрыв вторые производные от термодинамического потенциала, намагниченность, диэлектрическая проницаемость, модуль упругости, пирокоэффициент и т.п. Для описания кристалла претерпевающего фазовый переход второго рода Л.Д.Ландау ввел внутренний параметр кристалла, названный им параметром упорядочения. В простейшем случае им может быть величина смещения атомов.
3.3 Теория фазовых переходов Л.Д.Ландау применительно к сегнетоэлектрикам была развита В.Л.Гинзбургом и А.Ф.Девошниром. Роль параметра упорядочения играет поляризация Р. В окрестности точки фазового перехода, вследствие малости Р свободная энергия системы может быть разложена в ряд по степеням поляризации:
 (1)
(1)
где F0 - свободная энергия кристалла в неполярной параэлектрической фазе, для которой поляризация Р=0, a , b , g - коэффициенты разложения. В разложении (1) присутствуют только члены с четными степенями поляризации, т.к. свободная энергия не должна зависеть от направления вектора полярной оси. При фазовом переходе второго рода можно ограничиться членами четвертого порядка. Известно, что в состоянии равновесия свободная энергия; имеет минимум. т.е.
 (2)
(2)
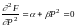 (3)
(3)
В (2), (3) равновесное значение поляризации P=P (спонтанная поляризация).
Из соотношения (2) следует два решения:
(1) Ps=0 (2) Ps2 = -a/b (4)
В точке фазового перехода P=О и значит при температуре Кюри Tc a=0. В окрестности Tc предполагается, что a линейно зависит от температуры
a=ac'(T-Tc) (5)
где
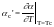 (6)
(6)
В теории показывается, что ac'=4/C, где С - константа Кюри, значение которой в основном определяется типом фазового перехода.
Тогда из (4) и (5) получим:
 (7)
(7)
Из (7) следует параболическая зависимость спонтанной поляризации P от температуры. Выражение (7) позволяет определить значение коэффициента b в разложении Ландау-Гинсбурга-Девоншира.
