
- •Вопрос 1
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4
- •При косвенном методе величина рассчитывается опосредованно, через другие величины, связанные с искомой определенной зависимостью. Относительные величины измеряются только косвенным методом.
- •Вопрос 5
- •Вопрос 6
- •Вопрос 7
- •Вопрос 8
- •Вопрос 9
- •Вопрос 10
- •Вопрос 11
- •Ч исло групп для удобства возьмем равным 3. Тогда величина интервала будет равна:
- •Вопрос 12
- •Пример: построим равнонаполненную группировку совокупности 20 студентов по признаку «посещаемость практических занятий» - х.
- •Вопрос 13
- •Сложные группировки (группировки по нескольким признакам) делятся на комбинационные и многомерные.
- •Комбинационная группировка студентов по признакам: оценка (y) и посещаемость практических занятий (X):
- •Вопрос 14
- •Вопрос 15
- •Вопрос 16
- •Кумулятивные ряды распределения – ряды распределения, которые содержат один или оба следующих элемента:
- •Вопрос 16 Графические представления рядов распределения
- •Вопрос 18 Понятие средней величины. Средняя арифметическая и ее свойства.
- •Вопрос 19
- •Понятие ведущего показателя
- •Вопрос 20
- •Вопрос 21
- •Вопрос 22
- •Вопрос 23
- •Вопрос 24 Показатели формы распределения. Ответ
- •Вопрос 25 Нормальное распределение и его свойства.
- •Вопрос 26
- •Вопрос 27
- •Вопрос 28
- •Вопрос 29
- •Вопрос 30
- •Вопрос 31 Способы отбора. Ответ
- •Вопрос 32
- •Вопрос 33
- •Вопрос 34
- •Вопрос 35
- •Вопрос 36 Количественная оценка тесноты связи по эмпирическим данным: эмпирический коэффициент детерминации, эмпирическое корреляционное отношение. Ответ
- •Вопрос 37 Количественная оценка тесноты связи по эмпирическим данным: коэффициент линейной парной корреляции. Ответ
- •Вопрос 38
- •Вопрос 39
- •Вопрос 40
- •Вопрос 41
- •Вопрос 42
- •Вопрос 43
- •Вопрос 44 Расчет параметров уравнения линейной множественной регрессии и их интерпретация.
- •Вопрос 45
- •Вопрос 46
- •Вопрос 47
- •Вопрос 48
- •Вопрос 49
- •Вопрос 50
- •Вопрос 51
- •Вопрос 52
- •Добыча нефти в Российской Федерации, млн.Тонн
- •Вопрос 53
- •Используется для правильной оценки значения полученного темпа прироста. Аi показывает какое абсолютное значение скрывается за относительным показателем 1% прироста.
- •Вопрос 54
- •Вопрос 55
- •Вопрос 56
- •Вопрос 57
- •Вопрос 58
- •Вопрос 59 Статистические методы прогнозирования
Вопрос 47
Виды индексов.
ОТВЕТ
Индексы, характеризующие изменение явления во времени представляют собой индексы динамики; индексы, характеризующие изменение явления в пространстве – территориальные индексы, индексы, характеризующие изменение явления по сравнению с эталоном - индексы выполнения плана.
Индексы объемных и качественных показателей.
Объемные индексы служат для измерения изменения объемных показателей. Объемные показатели выражаются абсолютными величинами (например, объем выпуска продукции, численность работающих).
Качественные индексы служат для измерения изменения качественных показателей. Качественный показатель определяется в расчете на количественную единицу. Примером таких показателей могут служить: цена, себестоимость единицы продукции, трудоемкость единицы продукции, производительность труда и т.п.
По степени охвата элементов явления индексы делятся на индивидуальные и сводные индексы.
Индивидуальный индекс характеризует изменение отдельных элементов, входящих в состав сложного явления. Например, изменение объема выпуска телевизоров определенной марки, рост или падение цен на акции в некотором акционерном обществе и т.д. Индивидуальные индексы обозначаются i и снабжаются подстрочным знаком индексируемого показателя: iq - индивидуальный индекс физического объема определенного вида продукции, ip – индивидуальный индекс цен на определенный вид продукции и т.д.
Индивидуальные
индексы рассчитываются как отношение
текущего уровня индексируемой величины
к базисному уровню индексируемой
величины:
![]() .
.
Например: ip =p1/p0 - индивидуальный индекс цен, где p1,p0 - цены единицы продукции текущего и базисного уровня; iq =q1/q0 - индивидуальный индекс физического объема продукции.
Сводный (общий) индекс характеризует изменение всех элементов сложного явления. Например, изменение физического объема продукции по предприятия в целом (предприятие выпускает разнокачественные товары); изменение цены по группе товаров (группа включает разнородные товары) и т.д.
Если индексы охватывают не все элементы явления, а лишь часть, то их называют групповыми или субиндексами (например, индексы продукции по отдельным отраслям промышленности).
Статистика применяет, главным образом, сводные и групповые индексы, которые и составляют особый прием исследования, именуемый индексным методом.
Сводный индекс обозначается буквой I и также сопровождается подстрочным знаком индексируемого показателя: например, Ip - сводный индекс цен; Iz - сводный индекс себестоимости.
Методика расчета сводных индексов сложнее, чем индивидуальных. Любые сводные индексы могут быть построены двумя способами: как агрегатные и как средние из индивидуальных.
Вопрос 48
Агрегатные индексы – основная форма индексов.
ОТВЕТ
Агрегатный индекс является основной формой индекса. «Агрегатным» он называется потому, что его числитель и знаменатель представляют собой набор – «агрегат» (от латинского aggregatus – складываемый, суммируемый) разнородных (т.е. непосредственно несопоставимых) элементов. Агрегатный индекс строится, как отношение сумм произведений двух величин: 1) индексируемой величины, 2) показателя-соизмерителя (веса индекса). Произведение индексируемой величины на вес индекса дает результативный показатель. Формула агрегатного индекса в общем виде:
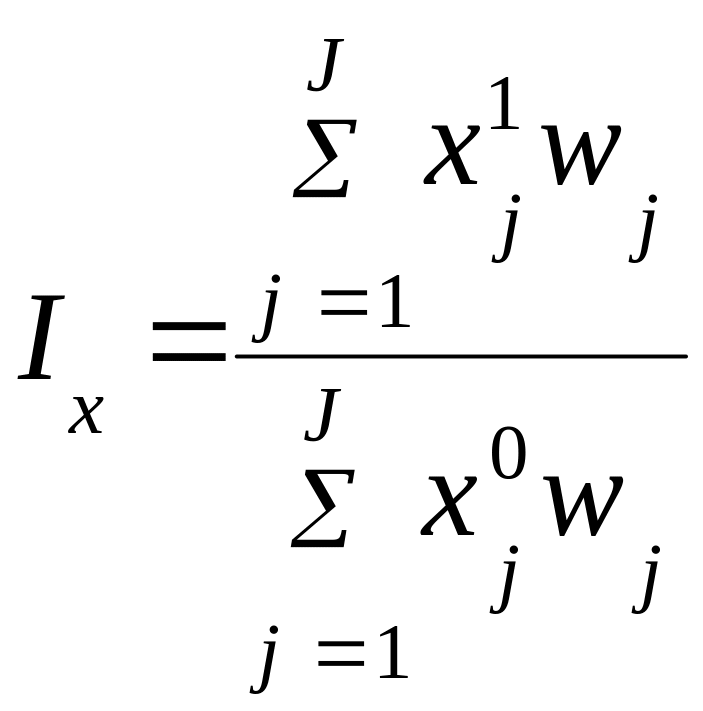 ,
,
где Х1j – сравниваемое (текущее) значение индексируемой величины у j-ого элемента, j=1;J,
Х0j – базисное значение индексируемой величины у j–ого элемента;
wj – показатель-соизмеритель (вес индекса) для j–ого элемента.
j – номер элемента, совокупность которых образует сложное явление (j=1;J).
Xj·wj – результативный показатель для j–ого элемента;
J- всего элементов в совокупности.
Весом индекса может быть показатель, относящийся к текущему, либо к базисному уровню.
Если в качестве весов брать значения признака-веса базисного уровня (w0), то формула агрегатного индекса примет вид:
 .
.
Ее называют агрегатной формой индекса Ласпейреса (по имени ученого Э.Ласпейреса, предложившего ее впервые в 1864 г.).
Если в качестве весов брать значения признака-веса текущего уровня, то формула агрегатного индекса примет вид:

Ее называют агрегатной формой индекса Пааше (по имени ученого Г.Пааше, предложившего ее впервые в в 1874 г.).
Проблема выбора весов индексирования.
В качестве веса индексирования при построении индекса объемного показателя выступает качественный показатель. Рассмотрим построение агрегатного индекса физического объема. В данном весом индексирования может быть либо p- цена, либо z-себестоимость, либо t-трудоемкость единицы продукции и т.п. Эти «соизмерители» дадут соответственно результативные показатели: стоимости, общих затрат, затрат времени на производство продукции.
Если
принять в качестве соизмерителя цену
базисного периода (р0),
то получим индекс физического объема
Ласпейреса:
 .
.
Если
принять в качестве соизмерителя цену
отчетного периода (р1),
то получим индекс физического объема
Пааше:
 .
.
Весом индексирования при построении индекса качественного показателя выступает объемный показатель. Рассмотрим построение агрегатного индекса цены за единицу продукции. В этом случае весом индекса будет физический объем выпуска - q. Результативный показателем при этом будет общая стоимость произведенной продукции.
Формула
агрегатного индекса цен Ласпейреса:

Формула
агрегатного индекса цен Пааше:
 .
.
Сводные индексы
результативных показателей представляют
собой отношение суммы результативных
показателей текущего уровня к сумме
результативных показателей базисного
уровня. Если результативный показатель
обозначить через j=xj·wj,
то его индекс будет:
 .
.
Например,
сводный индекс стоимости (Is)
(стоимость равна произведению физического
объема выпуска на цену: s=q·p) строится
как отношение суммарной стоимости
текущего уровня к суммарной стоимости
базисного уровня:
 .
.
Этот индекс показывает во сколько раз в среднем по совокупности возросла (уменьшилась) стоимость, текущего уровня по сравнению с базисным.
Значения агрегатных индексов, рассчитанные по формулам Ласпейреса и Пааше, редко совпадают. Для получения обобщенного показателя агрегатного индекса, дающего однозначное решение возможно:
Построить общий индекс на средних весах:
 .
.
2)
Построить общий индекс как среднее
геометрическое из индексов Ласпейреса
и Пааше:
 .
.
Этот способ предложил Фишер и назвал данную формулу «идеальным индексом».
3) Выбрать (предпочти) какой-то один вариант построения взаимосвязанных индексов. Данный подход был избран отечественной статистикой, в которой изменение объемных показателей измеряется по формуле Ласпейреса, а изменение качественных показателей – по формуле Пааше. То есть сводный индекс физического объема (Iq) рассчитывают по формуле Ласпейреса, а сводный индекс цены (Ip) по формуле Пааше.
