13.4. Задача композиции
Очень часто встречается функциональная зависимость вида
,
т.е. возникает
задача определения закона распределения
суммы компонент случайного вектора
по известному закону совместного
распределения его компонент
X
и Y.
Покажем, как эта задача решается в двух
случаях, когда компоненты
X
и Y:
1) СВДТ;
2) СВНТ.
1. Пусть
X
и Y
– СВДТ
с известным законом совместного
распределения
,
где
– множество возможных значений компоненты
X,
– множество возможных значений компоненты
Y.
Тогда закон распределения
записывается в виде
,
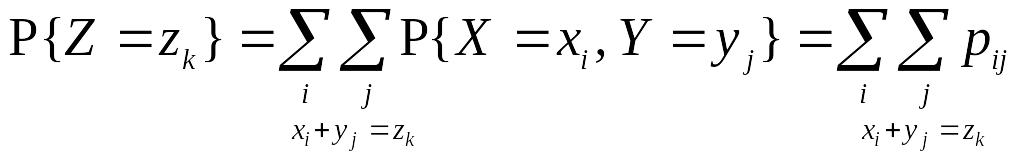где суммирование
распространяется на все значения
индексов i
и j,
для которых выполняется условие
.
Затем, построив ряд распределения
случайной величины Z
(исключая все те значения
,
вероятность которых равна нулю), можно
составить функцию распределения
.
Пример 11. Закон
распределения случайного вектора
задан таблицей:
Y X |
1 |
2 |
3 |
–1 |
|
0 |
|
1 |
|
|
0 |
Составив закон
распределения случайной величины
,
найти функцию
распределения
и вычислить
,
.
Решение. Найдем
вначале значения функции
:
,
,
,
,
,
.
Значит, случайная величина Z имеет пять возможных значений:
,
,
,
,
.
Вероятность
возможного значения
равна сумме вероятностей несовместных
событий
и
,
т.е.
.
Исключим значения
и
,
поскольку вероятности их равны нулю.
Поэтому ряд распределения случайной
величины Z
имеет вид:
Z |
0 |
2 |
3 |
P |
|
|
|
Тогда найдем функцию распределения :
Вычислим теперь и :
,
.
Ответ:
,
.
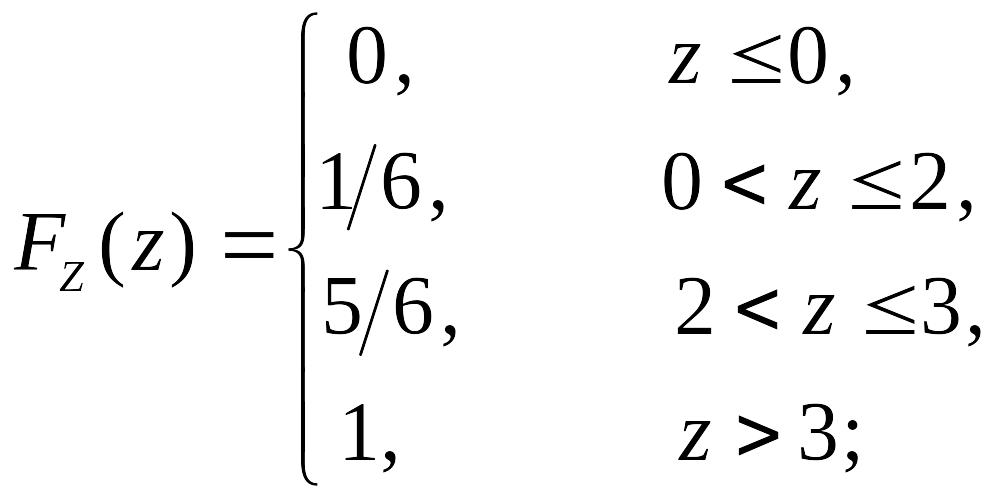
2. Пусть
X
и Y
– СВНТ
с известной плотностью совместного
распределения компонент
,
тогда
.
Особо важным для практики представляется частный случай, когда X и Y – независимые случайные величины, а . Получается так называемая задача композиции.
1. Пусть X и Y – независимые СВДТ, тогда
или
.
Пример 2.3.12. Рассматривается случайная величина Z – суммарное число «успехов» в двух независимых опытах с одной и той же вероятностью «успеха» p в каждом опыте. Найти закон распределения случайной величины Z и составить ее функцию распределения.
Решение. Пусть X – количество успехов в первом опыте, а Y – количество успехов во втором опыте. По условию задачи X и Y независимы. Тогда . Получается задача композиции. Поскольку случайные величины X и Y принимают только два значения 0 или 1, то случайная величина может принимать четыре значения
,
,
,
с вероятностями
,
qp,
pq,
соответственно. Тогда ряд распределения примет вид
Z |
0 |
1 |
2 |
P |
|
2pq |
|
Составим теперь функцию распределения случайной величины :
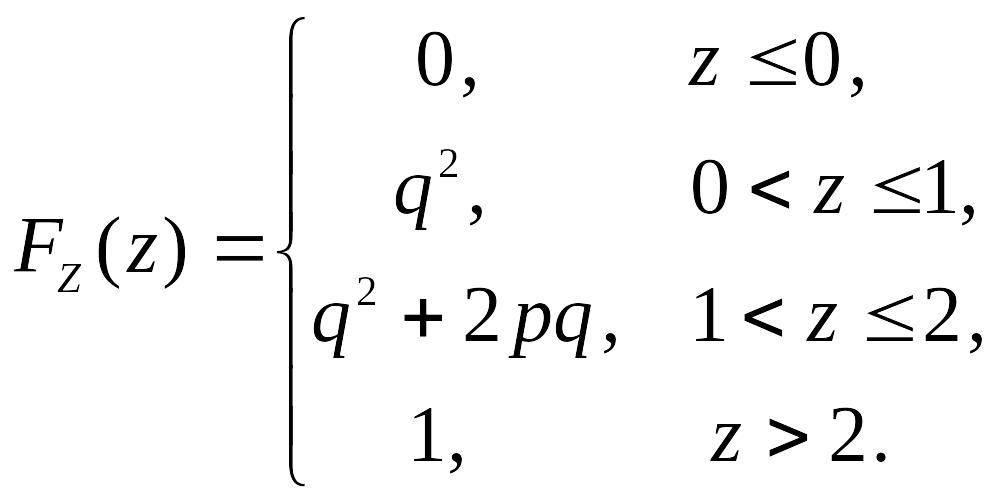
Ответ:
2. Пусть
X
и Y
– независимые
СВНТ,
и
– их плотности. Плотность совместного
распределения равна
.
Функция распределения суммы
равна
.
Этот интеграл можно вычислять как повторный:
Дифференцируя по z, получаем:
.
Две последние
формулы носят название формул
свертки. С
помощью этих формул можно выразить
функцию распределения
и плотность
суммы независимых случайных величин
через плотности и функции распределения
слагаемых. Отметим, что в силу симметрии
переменных x
и y
формулы свертки можно записать следующим
образом:
,
.
Пример 2.3.13. Пусть
случайные величины X
и Y
– независимы,
– функция распределения Х,
а Y
имеет плотность
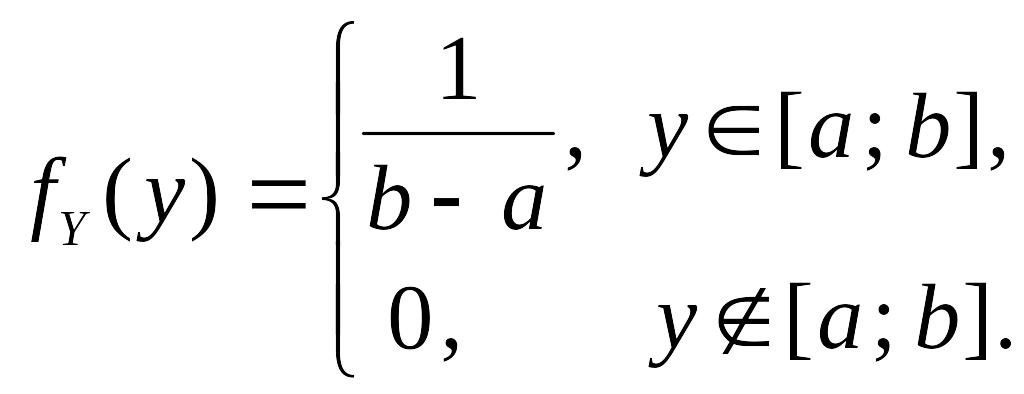
Составить функцию распределения и функцию плотности суммы .
Решение. Применяя формулу свертки, имеем
,
т.к. производная интеграла по переменной z равна значению подынтегральной функции от верхнего предела, умноженного на производную по z от верхнего предела, минус значение подынтегральной функции от нижнего предела, умноженного на производную по z от нижнего предела. Отсюда следует существование плотности
.
Ответ:
,
.
Пример 2.3.14. Случайные
величины X
и Y
независимы и равномерно распределены
на отрезке
:
,
.
Найти плотность вероятности случайной
величины
.
Решение. 1 способ. По
условию возможные значения X
определяются неравенством
,
возможные значения Y
– неравенством
.
Отсюда следует, что возможные случайные
точки
расположены в квадрате ABCD.
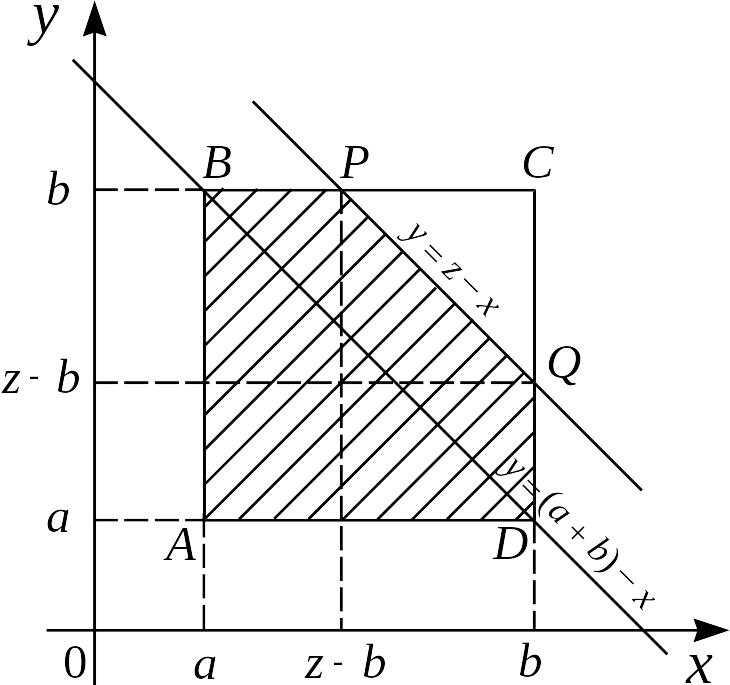
а б
Рис. 2.3.2.
По определению функции распределения
.
Неравенству
удовлетворяют те точки
плоскости xOy,
которые лежат ниже прямой
(эта прямая отсекает на осях Ox
и Oy
отрезки, равные z).
Если же брать только возможные значения
x
и y,
то неравенство
выполняется только для точек, лежащих
в квадрате ABCD
ниже прямой
.
С другой стороны, т.к. случайные величины X и Y независимы, то
,
где
область G
– часть квадрата ABCD,
которая расположена ниже прямой
,
а
– площадь G.
Очевидно, что величина площади
зависит от значения z.
Если
,
то
,
поэтому
.
Если
(рис. 2.3.2 а),
то
,
поэтому
.
Если
(рис. 2.3.2 б),
то
,
поэтому
.
Если
,
,
поэтому
.
Найдем
теперь плотность распределения
,
продифференцировав
по z:
График функции плотности так называемого треугольного распределения, или распределения Симпсона, показан на рис. 2.3.3.
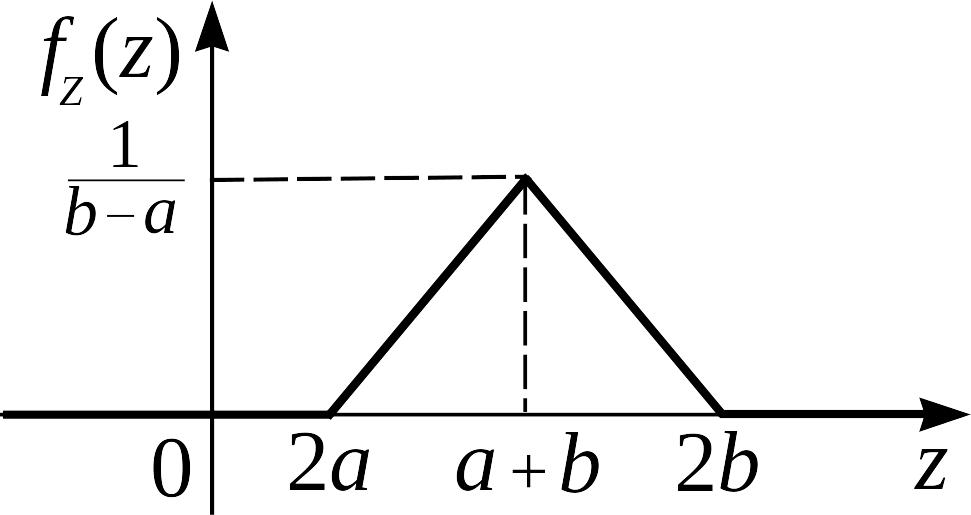
Рис. 2.3.3.
2 способ. Учтем,
что в данном случае подынтегральное
выражение в формуле свертки
отлично от нуля лишь в случае, когда
принадлежит отрезку
,
а именно:
,
если
;
,
если
.
Рассматривая два случая взаимного расположения отрезков, на которых плотности одновременно отличны от нуля (рис. 2.3.4), получим:
,
если
;
,
если
.
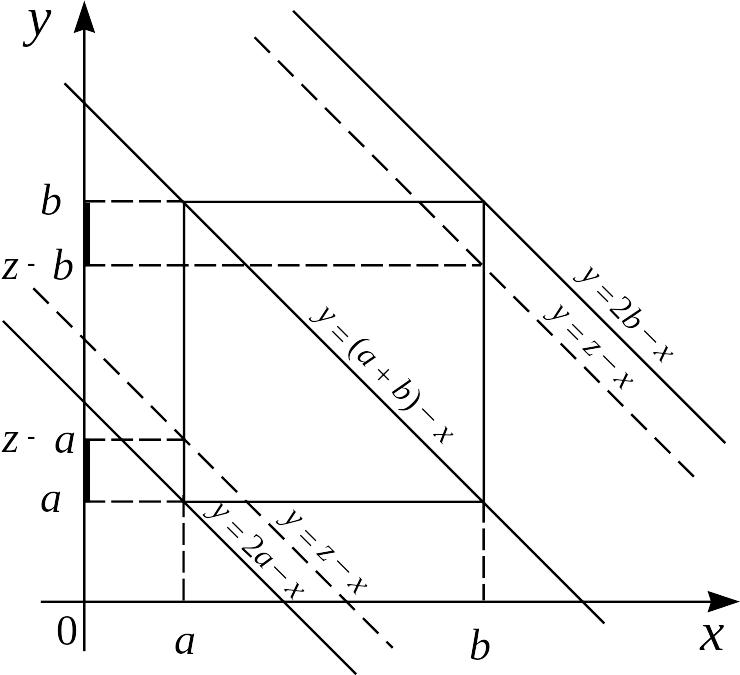
Рис. 2.3.4.
Ответ:
Определение. Закон
распределения W
определенного вида называется
композиционно
устойчивым,
если из того, что две независимые
случайные величины X
и Y
подчиняются закону распределения
данного типа, следует, что их сумма
подчиняется закону распределения W
того же вида (различаются только параметры
этого закона).
Рассмотрим примеры композиционно устойчивых распределений.
Пример 2.3.15. Найти
закон распределения суммы двух независимых
случайных величин X
и Y,
распределенных по закону Пуассона:
,
.
Решение. Найдем
вероятность события
,
где
:
.
Следовательно,
случайная величина
распределена по закону Пуассона с
параметром
.
Значит, распределение Пуассона
композиционно устойчиво.
Ответ:
.
Пример 2.3.16. Найти
закон распределения суммы двух независимых
случайных величин X
и Y,
распределенных по биномиальному закону:
,
.
Решение. Представим случайную величину X в виде:
,
где
(
)
– индикатор события A
в i-м
опыте:
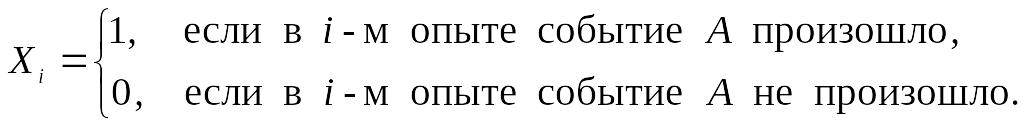
Ряд распределения случайной величины имеет вид:
|
0 |
1 |
P |
|
|
Аналогичное представление сделаем и для случайной величины Y:
,
где
(
)
– индикатор события A
в j-м
опыте:
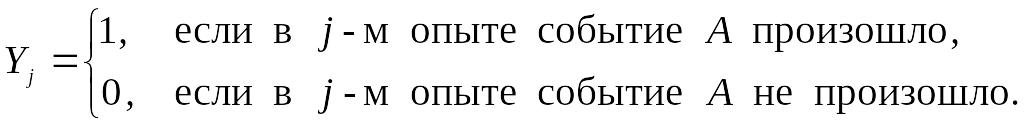
Ряд распределения случайной величины имеет вид:
|
0 |
1 |
P |
|
|
Следовательно,
,
где каждое из слагаемых является индикаторной случайной величиной распределенной по одному и тому же закону:
или |
0 |
1 |
P |
|
|
Всего слагаемых
–
.
Отсюда следует, что случайная величина
распределена по биномиальному закону
с параметрами
; p.
Значит, биномиальное распределение
композиционно устойчиво.
Ответ:
.
Замечание 1. Если вероятности p в различных сериях опытов (первая серия опытов описывается случайной величиной X, а вторая серия – случайной величиной Y) будут различны, то в результате сложения двух независимых случайных величин X и Y, распределенных по биномиальным законам, получится случайная величина Z, распределенная не по биномиальному закону.
Замечание 2. Примеры 2.3.15 и 2.3.16 легко обобщаются на произвольное число слагаемых (Проделайте выкладки самостоятельно!).
Пример 2.3.17. Случайные
величины X
и Y
независимы и нормально распределены:
,
.
Найти плотность вероятности случайной
величины
.
Решение. Пользуясь формулой свертки , получим:
.
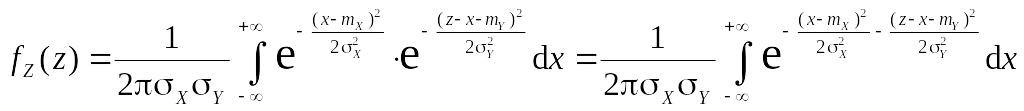Из курса интегрального исчисления известно, что
.
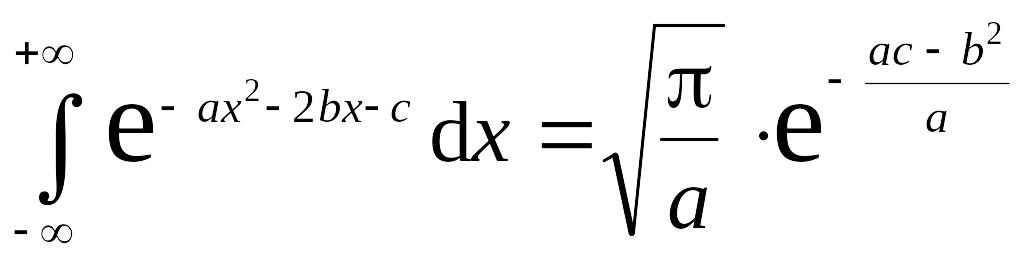В данном случае
,
,
.
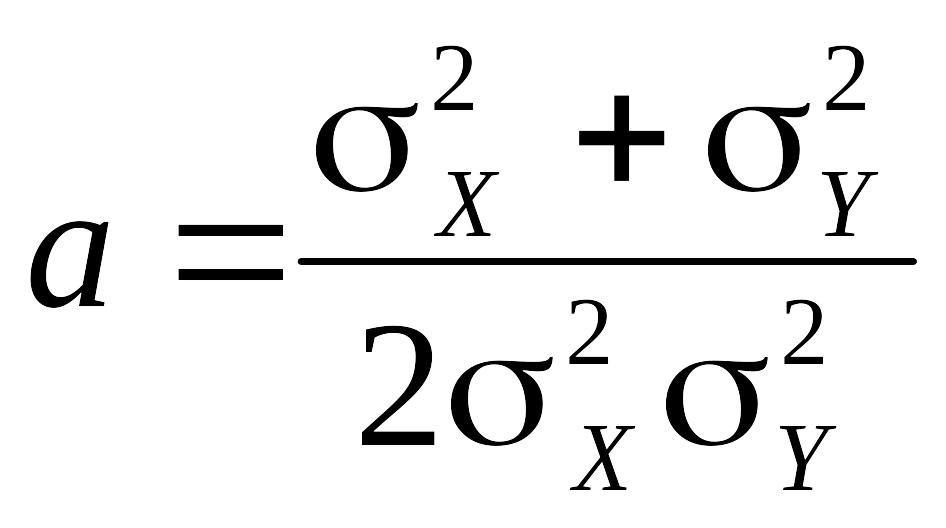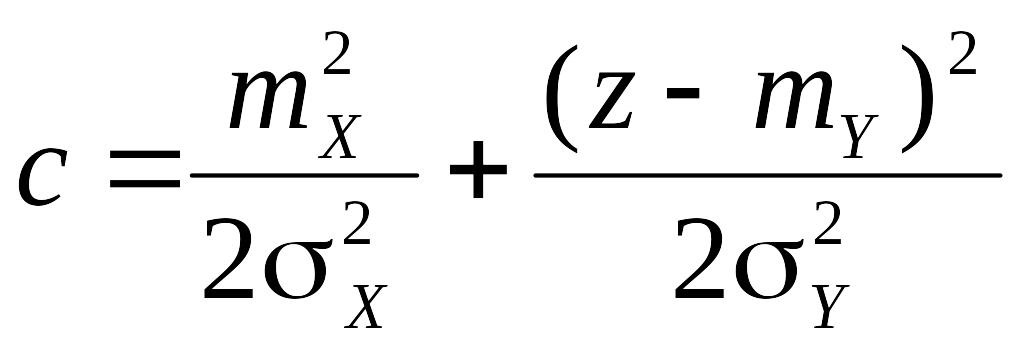Таким образом, из
структуры плотности следует, что
случайная величина
имеет нормальное распределение
,
где
,
.
Значит, нормальное распределение
композиционно устойчиво.
Ответ: , где , .
Упражнения
2.3.6. Независимые
случайные величины имеют биномиальное
распределение
,
.
Вычислить значение
,
если
.
2.3.7. Законы распределения случайных величин X и Y имеют вид:
X |
1 |
3 |
|
Y |
2 |
4 |
P |
0,3 |
0,7 |
|
P |
0,6 |
0,4 |
Найти распределение случайной величины .
2.3.8. Законы распределения случайных величин X и Y имеют вид:
X |
10 |
12 |
16 |
|
Y |
1 |
2 |
P |
0,4 |
0,1 |
0,5 |
|
P |
0,2 |
0,8 |
Найти распределение случайной величины .
2.3.9. Независимые
случайные величины имеют показательное
распределение
,
.
Найти плотность распределения случайной
величины
.
2.3.10. Независимые
случайные величины имеют равномерное
распределение
,
.
Найти функцию распределения и плотность
распределения случайной величины
.
2.3.11. Независимые
случайные величины имеют равномерное
распределение
,
.
Найти функцию распределения и плотность
распределения случайной величины
.
2.3.12. Случайные
величины X
и Y
независимы и нормально распределены:
,
.
Найти плотность вероятности случайной
величины
.
Ответы к упражнениям
2.3.6. 0,84.
2.3.7.
Z |
3 |
5 |
7 |
P |
0,18 |
0,54 |
0,28 |
2.3.8.
Z |
11 |
12 |
13 |
14 |
17 |
18 |
P |
0,08 |
0,32 |
0,02 |
0,08 |
0,1 |
0,4 |
2.3.9.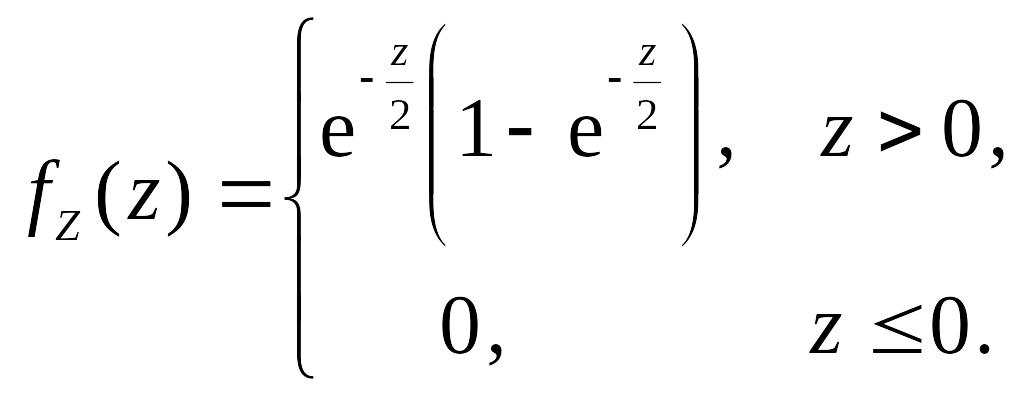 
2.3.10.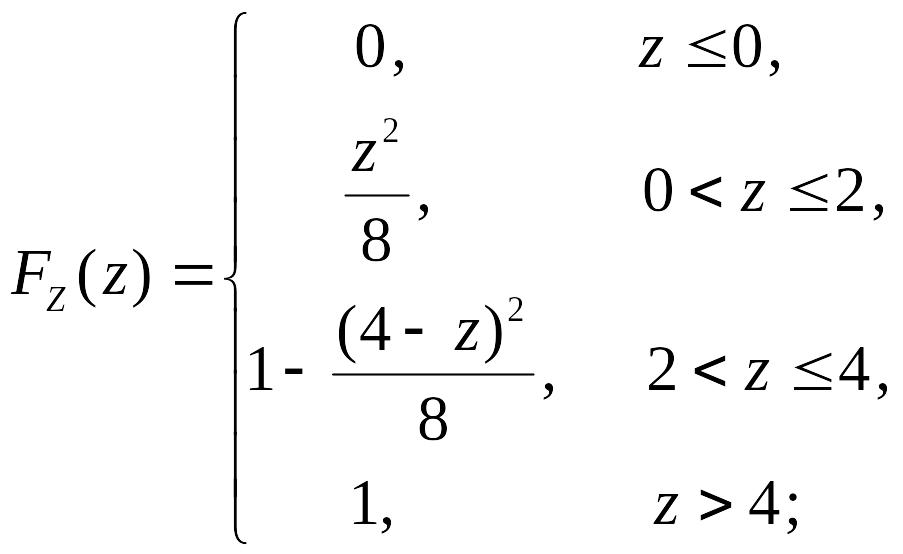 
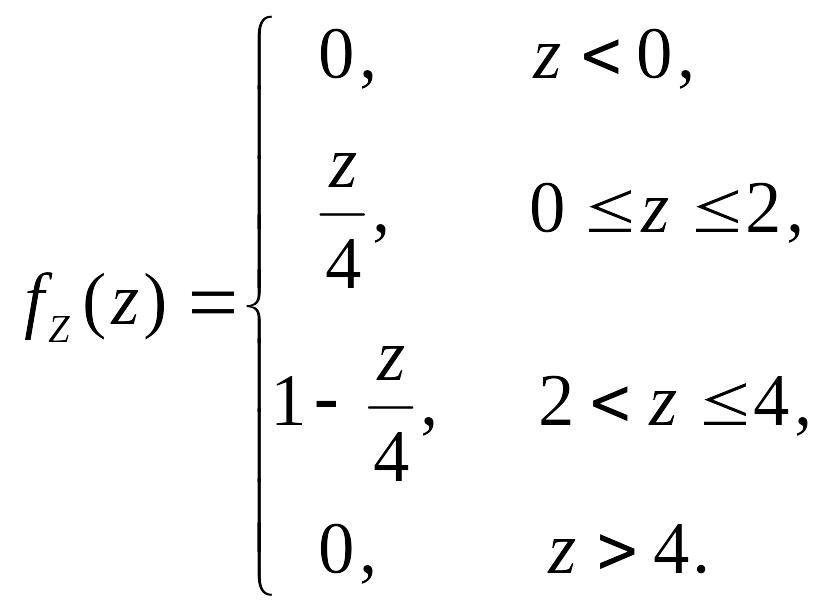
2.3.11.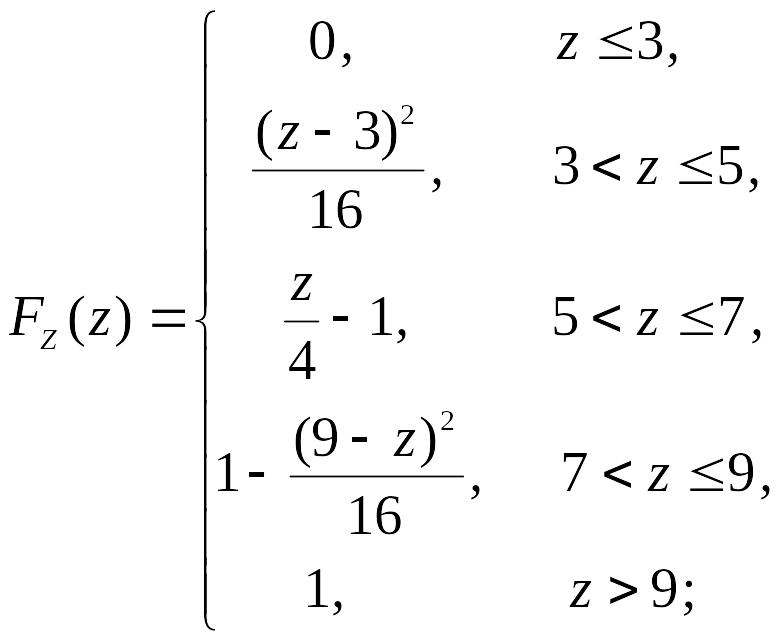 
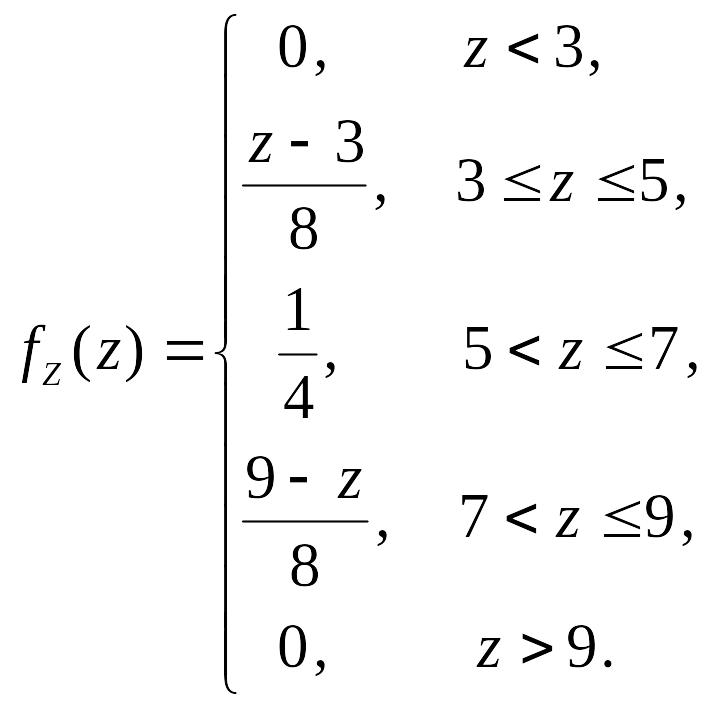
2.3.12. 
,
т.е.
.