13.2. Числовые характеристики функций одномерных случайных величин
Если X
– случайная величина с известным законом
распределения и
,
где
– неслучайная функция скалярного
аргумента x,
то математическое ожидание и дисперсия
случайной величины Y
(если они существуют) могут быть найдены
по следующим формулам:
,
если X
– СВДТ,
,
если X
– СВНТ;
,
если X
– СВДТ,
,
если X
– СВНТ.
Аналогичные формулы имеют место и для всех прочих начальных и центральных моментов распределения случайной величины .
Замечание 1. Таким образом, для вычисления числовых характеристик функции одномерной случайной величины X необязательно знать закон распределения случайной величины , а достаточно знать закон распределения случайного аргумента X.
Замечание 2. Если
,
то математическое ожидание случайной
величины
есть не что иное, как начальный момент
s-го
порядка, т.е.
.
Аналогично, если
,
то математическое ожидание случайной
величины
есть центральный момент s-го
порядка, т.е.
.
Пример 7. Закон распределения случайной величины X имеет вид:
X |
–1 |
0 |
1 |
2 |
P |
0,1 |
0,2 |
0,3 |
0,4 |
Вычислить
и
,
если
.
Решение. 1 способ (с помощью составления закона распределения случайной величины Y). Ряд распределения случайной величины Y имеет вид:
Y |
0 |
1 |
4 |
P |
0,2 |
0,4 |
0,4 |
Тогда
;
.
2 способ
(с помощью
формул
и
):
;
.
Ответ:
,
.
Пример 8. Случайная величина X задана плотностью распределения
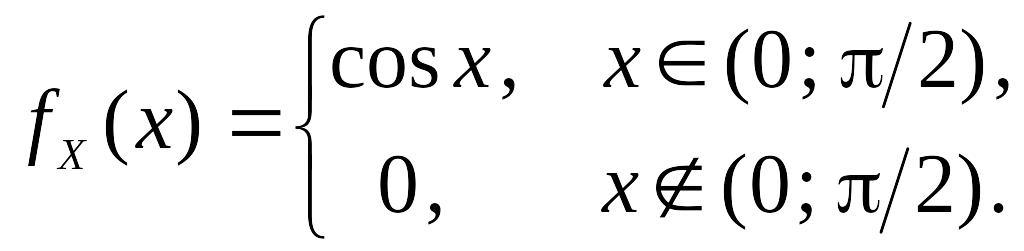
Найти математическое
ожидание и дисперсию функции
.
Решение. Найдем вначале математическое ожидание:
.
Вычислим теперь дисперсию:
.
Ответ:
,
.
Замечание. Математическое ожидание и дисперсию функции можно было вычислить, найдя предварительно плотность распределения случайной величины Y.
Упражнения
2.3.1. Закон распределения случайной величины X имеет вид:
X |
|
|
|
P |
0,2 |
0,7 |
0,1 |
Найти закон
распределения случайной величины
.
2.3.2. Число
X
неисправностей на участке высоковольтной
линии в течение года имеет распределение
Пуассона с параметром a
(
).
Общий материальный ущерб Y
от этих неисправностей пропорционален
квадрату их числа:
,
где
– неслучайная величина. Найти закон
распределения этого ущерба.
2.3.3. СВДТ
X
имеет пуассоновское распределение
,
а
.
Вычислить
.
2.3.4. Задана
плотность распределения
случайной величины X,
возможные значения которой заключены
в интервале
.
Найти плотность распределения
случайной величины Y,
если:
1) 
;
2) 
;
3) 
.
2.3.5. Задана
плотность распределения
случайной величины X,
возможные значения которой заключены
в интервале
.
Найти плотность распределения
случайной величины Y,
если:
1) 
;
2) 
;
3) 
.
Ответы к упражнениям
2.3.1.
Y |
|
1 |
P |
0,3 |
0,7 |
2.3.2.
Y |
0 |
k |
4k |
… |
|
… |
P |
|
|
|
… |
|
… |
2.3.3. 1.
2.3.4. 1)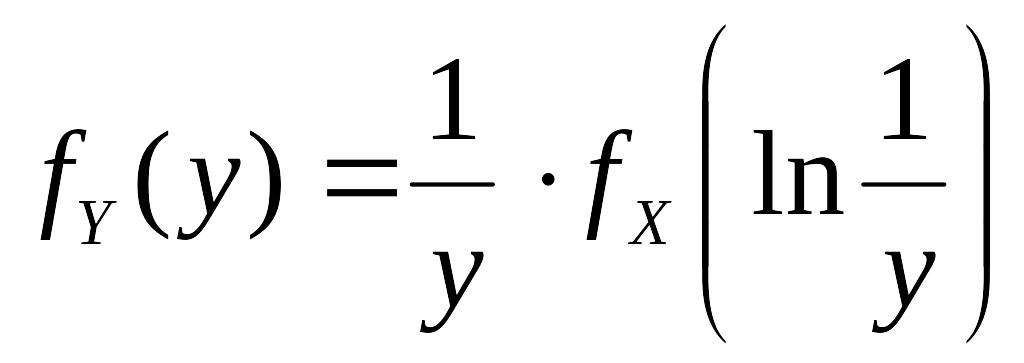 
,
;
2) 
,
;
3) 
,
.
2.3.5. 1) 
,
;
2) 
,
;
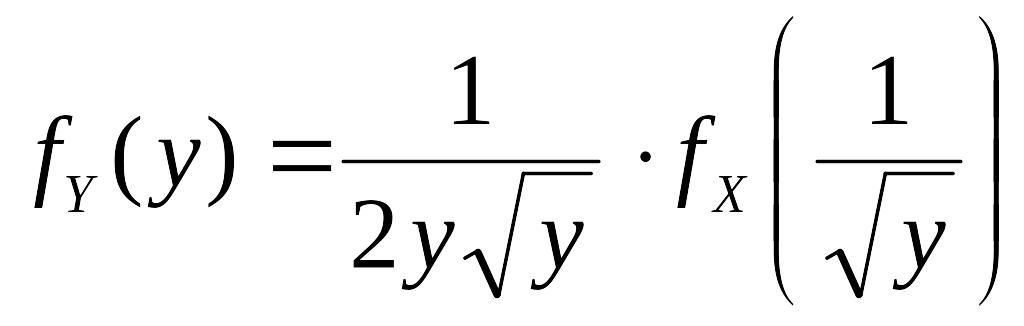3) 
,
.