13.3 Математическое ожидание функции одного случайного аргумента

Задана функция случайного аргумента X. Требуется найти математическое ожидание этой функ­ции, зная закон распределения аргумента.

1. Пусть аргумент X —дискретная случай­ная величина с возможными значениями , вероятности которых соответственно равны . Очевидно, Y —также дискретная случайная величина с возможными значениями . Так как событие «величина X приняла значение » влечет за собой событие «величина Y приняла значение », то вероятности возможных значений Y соответственно равны . Следовательно, математическое ожидание функции

Пример 1. Дискретная случайная величина X задана распределением

X	1	3	5
p	0.2	0.5	0.3

Найти математическое ожидание функции

Р е ш е н и е.

Найдем возможные значения Y:

Y	2	10	26
p	0.2	0.5	0.3

2. Пусть аргумент X—непрерывная случайная величина, заданная плотностью распределения f(x). Для отыскания математического ожидания функции можно сначала найти плотность распределения g(y) величины Y, а затем воспользоваться формулой

Если отыскание функции g(y) является затруднительным, то можно непосредственно найти математиче­ское ожидание функции по формуле

В частности, если возможные значения X принадлежат интервалу (а, b), то

(*)

Пример 2. Непрерывная случайная величина X задана плотностью распределения

f(x) = sinx в интервале ; вне этого интервала f(x) = 0. Найти математическое ожидание функции .

Решение. Воспользуемся формулой (*). По условию, f(x) = sinx, , a = 0, b = n/2. Следовательно,

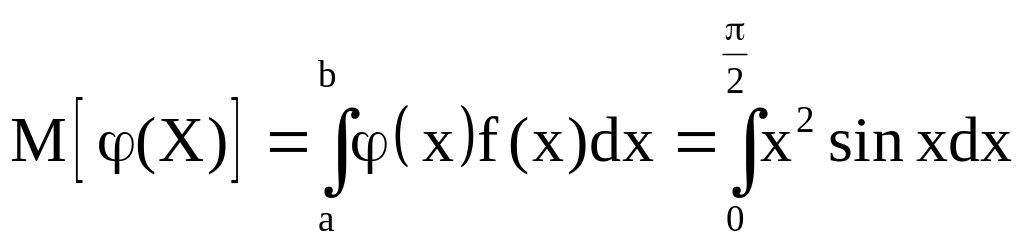
Интегрируя по частям, получим искомое математическое ожидание

13.4. Функция двух случайных аргументов. Распределение суммы независимых слагаемых.

Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное зна­ние случайной величины Z, то Z называют функцией двух случайных аргументов X и Y:

.

Покажем на примерах, как найти рас­пределение функции по известным распреде­лениям слагаемых. Такая задача часто встречается на практике. Например, если X — погрешность показаний измерительного прибора (распределена нормально), Y — погрешность округления показаний до ближайшего деле­ния шкалы (распределена равномерно), то возникает задача — найти закон распределения суммы погрешностей

1. Пусть X и Y—дискретные независимые случайные величины. Для того чтобы составить закон распределения функции Z = X+Y, надо найти все возможные значения Z и их вероятности.

Пример 1. Дискретные независимые случайные величины заданы распределениями:

X	3	4		Y	1	2
p	0.2	0.8		p	0.4	0.6

Составить распределение случайной величины Z = X+Y.

Решение.

Возможные значения Z есть суммы каждого возмож­ного значения X со всеми возможными значениями Y:

При , вероятность совместного наступления независимых X= и Y= , равна произведению вероятностей

.

Искомое распределение Z = X+Y,

Z	4	5	6
p	0.08	0.44	0.48

Контроль: 0,08 + 0,44+0,48=1.

2. Пусть X и Y—непрерывные случайны величины. Доказано: если X и Y независимы, плотность распределения g(z) суммы Z = X + Y при условии, что плотность хотя бы одного из аргументов задана на интервале (— , ) одной формулой) быть найдена с помощью равенства

где — плотности распределения аргументов.

Плотность распределения суммы независимых случай­ных величин называют композицией.