1.5. Первый закон термодинамики

Одним из основных законов природы является закон со­хранения и превращения энергии. Впервые он был сформули­рован в середине XVIII в. М. В. Ломоносовым.

Первый закон термодинамики является частным случаем закона сохранения и превращения энергии применительно к процессам взаимного превращения различных видов энергии, включая теплоту и работу. Он утверждает: энергия изолиро­ванной термодинамической системы остается неизменной, не­зависимо от того, какие процессы в ней протекают.

Термодинамическим процессом принято называть совокуп­ность последовательных состояний рабочего тела при его тепломеханическом взаимодействии с окружающей' средой. Для того чтобы к любому мгновенному состоянию рабочего тела в термодинамическом процессе можно было применить уравнение состояния, термодинамический процесс должен быть равновесным, т. е. он должен протекать при бесконечно малых разностях давлений и температур как в самом рабо­чем теле, так и между рабочим телом и окружающей средой. Для достижения равновесности процесс должен совершаться бесконечно медленно. Так как все реальные процессы проис­ходят при конечных разностях давлений и температур, то все они неравновесны.

Обратимыми называются такие термодинамические процес­сы, которые могут быть проведены как в прямом направлении (например, расширение), так и в обратном (сжатие) через одну и ту же последовательность промежуточных состоянии с возвращением в исходное состояние как самого рабочего те­ла, так и окружающей среды. Обратимый процесс должен быть равновесным и происходить без трения и вихреобразования, для того чтобы работа не превращалась необратимо в теплоту. Поскольку в природе все реальные процессы не­равновесны, то, следовательно, они и необратимы.

В зависимости от условий и характера протекания реаль­ные процессы в той или иной степени приближаются к равно­весным, причем эта степень приближения тем больше, чем медленнее протекают реальные процессы и чем меньше раз­ность между параметрами рабочего тела и окружающей сре­дой. Иными словами, обратимые процессы являются некото­рым пределом, к которому в известной степени точности при­ближаются все необратимые реальные процессы.

- При рассмотрении термодинамического процесса в самом общем случае подводимая к рабочему телу теплота Q рас­ходуется на изменение внутренней энергии Ли и совершение механической работы L, поэтому математическое выражение первого закона термодинамики для произвольного количест­ва рабочего тела

Q = Δu + L, (1.29)

для 1 кг рабочего тела

q = Δи + l,

в дифференциальной форме

dq = du + dl.

Под внутренней энергией газа понимают сумму кинетиче­ской и потенциальной энергии атомов и молекул. Первая обу­словлена скоростью движения и массой частиц, вторая — их взаимным расположением и силами взаимодействия между ними.

Внутренняя энергия реального газа является функцией со­стояния газа, т. 'е. функцией его параметров состояния, поэто­му изменение ее в термодинамическом процессе не зависит от характера процесса, а определяется только начальными и ко­нечными значениями параметров состояния, т. е.

С помощью уравнения состояния любой из параметров мо­жет быть выражен через два других, поэтому изменение вну­тренней энергии можно выразить функцией двух любых пара­метров состояния.

Внутренняя энергия идеального газа является функцией температуры газа и от давления не зависит:

Для 1 кг идеального газа изменение внутренней энергии

(1.30)

где C_v — теплоемкость газа при v = const.

Для элементарного процесса

du = CvdT (1.31)

Механическая работа L газа зависит от характера ,процесса.

Рассмотрим работу произвольного количества газа М (кг) в цилиндре при перемещении поршня с площадью f на рас­стояние dS (рис. 1.1). Ввиду малости dS будем считать дав­ление в цилиндре в процессе этого элементарного перемеще­ния поршня постоянным и равным Р. Тогда абсолютная рабо­та, совершаемая газом при расширении, т. е. работа переме­щения поршня под действием силы F = f-P равна dL = FdS = = PfdS. Изменение объема dV = fdS, следовательно, dL = PdV. Графически элементарная работа dL (см. рис. 1.1) соответствует заштрихованной площадке.

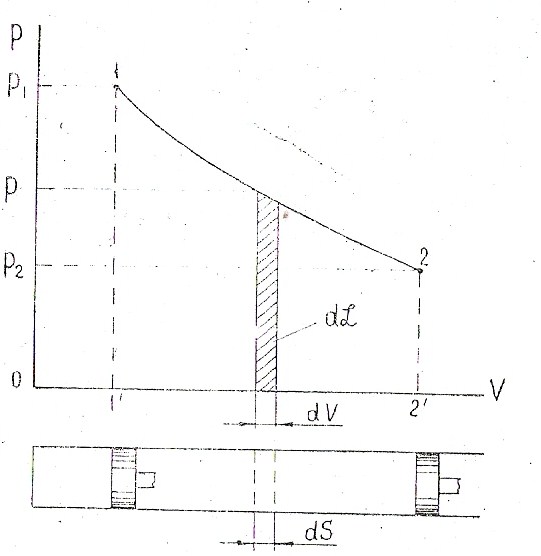
Рис. 1.1 Графический способ определения механической работы

Для 1 кг газа эле­ментарная механи­ческая работа газа

dl = Pdv. (1.32)

Если величина Р переменная, то пол­ную работу на учас­тке 1...2 процесса (см. рис. 1.1 ) опре­деляем как

Работа L на учас­тке 1....2 в PV коор­динатах соответст­вует площади 1 — 2—2'—Г, располо­женной под кривой, характеризую щей процесс.

Для 1 кг газа

(1.33)

Необходимо учитывать, что полученные для определения механической работы формулы справедливы только для рав­новесных и обратимых процессов. Площадь, ограниченная кривой, характеризующей процесс в. РV-координатах, соот­ветствует работе только обратимого процесса.

При необратимых процессах часть работы превращается в теплоту, поэтому работу необратимого процесса нельзя определить по приведенным формулам. Площадь, ограничен­ная кривой, характеризующей процесс в РV-координатах, не соответствует действительной работе.

учетом соотношения (1.32) для элементарной механи­ческой работы газа дифференциальное выражение первого закона термодинамики имеет вид:

dq = du.+ dl = c,dT + Pdv. (1.34)

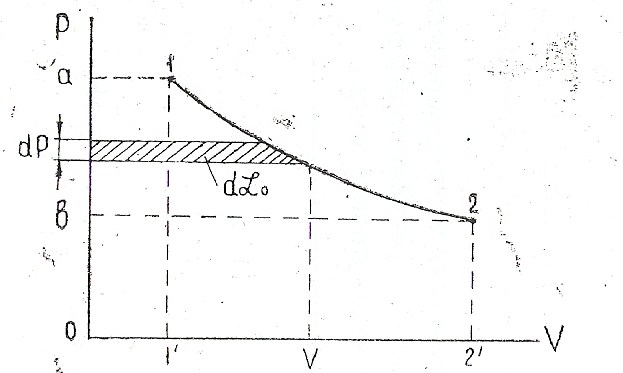
Рис. 1.2. Графический способ определения располагаемой работы.

Для конечного процесса с 1 кг газа

(1.35)

Если учесть, что дифференциальное выражение работы Pdv может быть представлено в виде разности d(Pv)-vdP, то равенство (1.34) примет вид:

dq = du + d(Pv) - vdP = d(u + Pv) - vdP.

Сумма внутренней энергии и и произведение Pv представ­ляют собой функцию состояния газа, называемую энтальпией:

(1.36)

где Pv — работа проталкивания, численно равная работе, кото­рую необходимо затратить, чтобы объем v «протолкнуть» с давлением Р. Таким образом, с учетом равенства (1.36) диф­ференциальное выражение первого закона термодинамики имеет вид:

dq = di - vdP = c_pdT – υdP.

Это выражение в сравнении с равенством (1.34) называют второй формой дифференциального выражения первого зако­на термодинамики. Произведение vdP представляет собой не­которую элементарную работу, которая на рис. 1.2 представ­лена заштрихованной площадкой. Эту работу в отличие от механической работы газа называют располагаемой, или тех­нической работой. Располагаемая работа конечного процесса 1...2 произвольной массы газа

L₀ =−

Для 1 кг газа

l₀= −

Чтобы работа процесса с понижением давления была по­ложительной (dP<0), принят знак минус.

Располагаемая, или техническая работа газа lо представ­ляет собой работу, получаемую или затраченную при пере­несении массы газа в область с более низким или с более вы­соким давлением. Она является результатом трех работ. На рис. 1.2 показан графический способ определения работы га­за при понижении давления:

l₀ = пл· а12b = пл·all'0 + пл·122'1' - пл·2b02' = P₁υ₁ + υ – P₂υ₂ = P₁υ₁– P₂υ₂ + l.

Площадь a — 1 — 1' — 0 соответствует работе процесса на­полнения цилиндра газом при давлении Р_{. Работа, соответ­ствующая площади 2 — b — 0 — 2', характеризует процесс вы­талкивания газа из цилиндра после совершения механической работы в процессе расширения. Рассмотренная совокупность процессов соответствует рабочему процессу газовой турбины, совершающей полезную работу при понижении давления газа.

Обратная последовательность процессов с наполнением цилиндра при низком давлении с последующими процессами сжатия и выталкивания из цилиндра сжатого газа при более высоком давлении соответствует рабочему процессу компрес­сорных машин. Таким образом, для конечного процесса вто­рое выражение первого закона термодинамики принимает вид:

Выражение первого закона термодинамики, приведенное в виде соотношения (1.29), справедливо для процессов, в кото­рых газ не имеет перемещения в пространстве. В случае дви­жения газа, теплота, подводимая к нему, в самом общем слу­чае будет затрачиваться на изменение его внутренней и кине­тической энергии, а также на совершение работы против внешних сил. Поэтому первый закон термодинамики для одно­го килограмма движущегося газа можно записать в виде

где dl_пр—работа против внешних сил в рассматриваемом процессе с подводом теплоты dq; d(ω²/2) — изменение кине­тической энергии.

Работа проталкивания в элементарном процессе dl_пр= d(Pv), а сумма du + d(Pv) = di, следовательно, dq = di + d(ω ²/2).

Для идеального газа

dq = _CpdT + d(ω ²/2)

или

Для конечного процесса

Из равенства (1.38) следует, что при движении газа с по­стоянной скоростью, когда ω ₂ = ω₁, подводимая к газу тепло­та будет затрачиваться на увеличение его энтальпии, так как в этом случае q = i₂ — i₁.

В случае если течение газа происходит без подвода тепло­ты, q = 0, изменение кинетической энергии газа равно:

Задачи

1. Найти объемную теплоемкость кислорода при постоян­ном объеме и постоянном давлении, считая С = const.

Для двухатомных газов μCv = 20,93 кДж/(кмоль·К); μCp = 29,31 кДж/(кмоль·К). Следовательно, для кислорода (и любого двухатомного газа)

2. Вычислить среднюю теплоемкость с для воздуха при постоянном давлении в пределах 200...800°С, считая зависи­мость теплоемкости от температуры нелинейной (криволи­нейной).

Решение

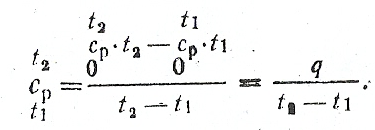
800

Из таблиц средняя теплоемкость с_р =1,0710 кДж/(кг-К);

0

200

с_р= 1,0115 кДж/(кг·К), тогда

0

200

с_р= =1.091кДж/(кг·К).

0

3. Решить предыдущую задачу, считая зависимость тепло­емкости от температуры линейной.